 , so we can
deduce that the momentum conjugate to this coordinate is conserved.
An explicit expression for the momentum conjugate to
, so we can
deduce that the momentum conjugate to this coordinate is conserved.
An explicit expression for the momentum conjugate to  is
is
The kinetic energy, expressed in terms of a suitable set of generalized coordinates, is a Lagrangian for a free rigid body. In section 2.1 we found that the kinetic energy of a rigid body can be written as the sum of the rotational kinetic energy and the translational kinetic energy. If we choose one set of coordinates to specify the position and another set to specify the orientation, the Lagrangian becomes a sum of a translational Lagrangian and a rotational Lagrangian. The Lagrange equations for translational motion are not coupled to the Lagrange equations for the rotational motion. For a free rigid body the translational motion is just that of a free particle: uniform motion. Here we concentrate on the rotational motion of the free rigid body. We can adopt the Euler angles as the coordinates that specify the orientation; the rotational kinetic energy was expressed in terms of Euler angles in the previous section.
The Lagrangian for a free rigid body has no explicit time dependence, so we can deduce that the energy, which is just the kinetic energy, is conserved by the motion.
The Lagrangian does not depend on the Euler angle  , so we can
deduce that the momentum conjugate to this coordinate is conserved.
An explicit expression for the momentum conjugate to
, so we can
deduce that the momentum conjugate to this coordinate is conserved.
An explicit expression for the momentum conjugate to  is
is
(define Euler-state
(up 't
(up 'theta 'phi 'psi)
(up 'thetadot 'phidot 'psidot)))
(show-expression
(ref (((partial 2) (T-rigid-body 'A 'B 'C)) Euler-state)
1))
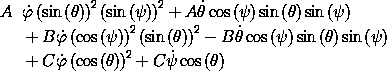
We know that this complicated quantity is conserved by the motion of the rigid body because of the symmetries of the Lagrangian.
If there are no external torques, then we
expect that the vector angular momentum will be conserved. We can
verify this using the Lagrangian formulation of the problem. First,
we note that Lz is the same as p . We can check this by
direct calculation:
. We can check this by
direct calculation:
(print-expression
(- (ref ((Euler-state->L-space 'A 'B 'C) Euler-state)
2)
(ref (((partial 2) (T-rigid-body 'A 'B 'C)) Euler-state)
1)))
;Value: 0
We know that p is conserved because the Lagrangian for the free
rigid body did not mention
is conserved because the Lagrangian for the free
rigid body did not mention  , so now we know that Lz is
conserved. Since the orientation of the coordinate axes is arbitrary,
we know that if any rectangular component is conserved then all of
them are. So the vector angular momentum is conserved for the free
rigid body.
, so now we know that Lz is
conserved. Since the orientation of the coordinate axes is arbitrary,
we know that if any rectangular component is conserved then all of
them are. So the vector angular momentum is conserved for the free
rigid body.
We could have seen this with the help of Noether's theorem (see section 1.8.4). There is a continuous family of rotations that can transform any orientation into any other orientation. The orientation of the coordinate axes we used to define the Euler angles is arbitrary, and the kinetic energy (the Lagrangian) is the same for any choice of coordinate system. Thus the situation meets the requirements of Noether's theorem, which tells us that there is a conserved quantity. In particular, the family of rotations around each coordinate axis gives us conservation of the angular momentum component on that axis. We construct the vector angular momentum by combining these contributions.
Exercise 2.10. Vector angular momentum
Fill in the details of the argument that Noether's theorem implies
that vector angular momentum is conserved by the motion of the free
rigid body.
Lagrange's equations for the motion of a free rigid body in terms of Euler angles are quite disgusting, so we will not show them here. However, we will use the Lagrange equations to explore the motion of the free rigid body.
Before doing this it is worth noting that the equations of motion
in Euler angles are singular for some configurations, because for these
configurations the Euler angles are not uniquely defined. If we set
 = 0 then an orientation does not correspond to a unique value
of
= 0 then an orientation does not correspond to a unique value
of  and
and  ; only their sum determines the orientation.
; only their sum determines the orientation.
The singularity arises in the explicit Lagrange equations when we
attempt to solve for the second derivative of the generalized coordinates in
terms of the generalized coordinates and the generalized velocities
(see section 1.7). The isolation
of the second derivative requires multiplying by the inverse of
 2
2  2 L. The determinant of this quantity
becomes zero when the Euler angle
2 L. The determinant of this quantity
becomes zero when the Euler angle  is zero:
is zero:
(show-expression
(determinant
(((square (partial 2)) (T-rigid-body 'A 'B 'C))
Euler-state)))
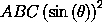
So when  is zero, we cannot solve for the second derivatives.
When
is zero, we cannot solve for the second derivatives.
When  is small, the Euler angles can move very rapidly, and
thus may be difficult to compute reliably. Of course, the motion of
the rigid body is perfectly well behaved for any orientation. This is
a problem of the representation of that motion in Euler angles; it is a
``coordinate singularity.''
is small, the Euler angles can move very rapidly, and
thus may be difficult to compute reliably. Of course, the motion of
the rigid body is perfectly well behaved for any orientation. This is
a problem of the representation of that motion in Euler angles; it is a
``coordinate singularity.''
One solution to this problem is to use another set of Euler-like coordinates for which Lagrange's equations have singularities for different orientations, such as those defined in equation (2.40). So if as the calculation proceeds the trajectory comes close to a singularity in one set of coordinates, we can switch coordinate systems and use another set for a while until the trajectory encounters another singularity. This solves the problem, but it is cumbersome. For the moment we will ignore this problem and compute some trajectories, being careful to limit our attention to trajectories that avoid the singularities.
We will compute some trajectories by numerical integration and check our integration process by seeing how well energy and angular momentum are conserved. Then, we will investigate the evolution of the components of angular momentum on the principal axis basis. We will discover that we can learn quite a bit about the qualitative behavior of rigid bodies by combining the information we get from the energy and angular momentum.
To develop a trajectory from initial conditions we integrate the Lagrange equations, as we did in chapter 1. The system derivative is obtained from the Lagrangian:
(define (rigid-sysder A B C)
(Lagrangian->state-derivative (T-rigid-body A B C)))
The following program monitors the errors in the energy and the components of the angular momentum:
(define ((monitor-errors win A B C L0 E0) state)
(let ((t (time state))
(L ((Euler-state->L-space A B C) state))
(E ((T-rigid-body A B C) state)))
(plot-point win t (relative-error (ref L 0) (ref L0 0)))
(plot-point win t (relative-error (ref L 1) (ref L0 1)))
(plot-point win t (relative-error (ref L 2) (ref L0 2)))
(plot-point win t (relative-error E E0))))
(define (relative-error value reference-value)
(if (zero? reference-value)
(error "Zero reference value -- RELATIVE-ERROR")
(/ (- value reference-value) reference-value)))
We make a plot window to display the errors:
(define win (frame 0. 100. -1.e-12 1.e-12))
The default integration method used by the system is Bulirsch-Stoer (bulirschstoer), but here we set the integration method to be quality-controlled Runge-Kutta (qcrk4), because the error plot is more interesting:
(set! *ode-integration-method* 'qcrk4)
We use evolve to investigate the evolution:
(let ((A 1.) (B (sqrt 2.)) (C 2.) ; moments of inertia
(state0 (up 0.0 ; initial state
(up 1. 0. 0.)
(up 0.1 0.1 0.1))))
(let ((L0 ((Euler-state->L-space A B C) state0))
(E0 ((T-rigid-body A B C) state0)))
((evolve rigid-sysder A B C)
state0
(monitor-errors win A B C L0 E0)
0.1 ; step between plotted points
100.0 ; final time
1.0e-12))) ; max local truncation error
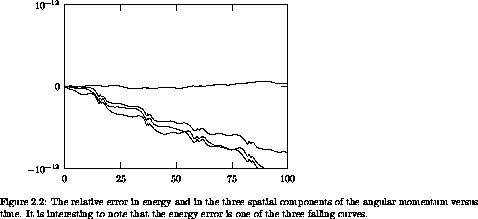
The plot that is developed of the relative errors in the components of the angular momenta and the energy (see figure 2.2) shows that we have been successful in controlling the error in the conserved quantities. This should give us some confidence in the trajectory that is evolved.
The evolution of the components of the angular momentum on the principal axes has a remarkable property. For almost every initial condition the body components of the angular momentum periodically trace a simple closed curve.
We can see this by investigating a number of trajectories and plotting the components of angular momentum of the body on the principal axes (see figure 2.3). To make this figure a number of trajectories of equal energy were computed. The three-dimensional space of body components is projected onto a two-dimensional plane for display. Points on the back of this projection of the ellipsoid of constant energy are plotted with lower density than points on the front of the ellipsoid. For most initial conditions we find a one-dimensional simple closed curve. Some trajectories on the front side appear to cross trajectories on the back side, but this is an artifact of projection. There is also a family of trajectories that appear to intersect in two points, one on the front side and one on the back side. The curve that is the union of these trajectories is called a separatrix; it separates different types of motion.

What is going on? The state space for a free rigid body is six-dimensional: the three Euler angles and their time derivatives. We know four constants of the motion -- the three spatial components of the angular momentum, Lx, Ly, and Lz, and the energy, E. Thus, the motion is restricted to a two-dimensional region of the state space.9 Our experiment shows that the components of the angular momentum trace one-dimensional closed curves in the angular-momentum subspace, so there is something more going on here.
The total angular momentum is conserved if all of the components are, so we also have the constant

The spatial components of the angular momentum do not change, but of course the projections of the angular momentum onto the principal axes do change because the axes move as the body moves. However, the magnitude of the angular momentum vector is the same whether it is computed from components on the fixed basis or components on the principal axis basis. So, the combination

is conserved.
Using the expressions (2.53-2.55) for the angular momentum in terms of the components of the angular velocity vector on the principal axes, the kinetic energy (2.30) can be rewritten in terms of the angular momentum components on the principal axes:

The two conserved quantities (2.57 and 2.58) provide constraints on how the components of the angular momentum vector on the principal axes can change. We recognize the angular momentum integral (2.57) as the equation of a sphere, and the kinetic energy integral (2.58) as the equation for a triaxial ellipsoid. Both integrals are conserved so the components of the angular momentum are constrained to move on the intersection of these two surfaces, the energy ellipsoid and the angular momentum sphere. The intersection of an ellipsoid and a sphere with the same center is generically two closed curves, so an orbit is confined to one of these curves. This sheds light on the puzzle posed at the beginning of this section.
Because of our ordering A < B < C, the longest axis of this
triaxial ellipsoid coincides with the  direction if all
the angular momentum is along the axis of largest principal moment of
inertia, and the shortest axis of the energy ellipsoid coincides with
the hata axis if all the angular momentum is along the
smallest moment of inertia. Without actually solving the Lagrange
equations, we have found strong constraints on the evolution of the
components of the angular momentum on the principal axes.
direction if all
the angular momentum is along the axis of largest principal moment of
inertia, and the shortest axis of the energy ellipsoid coincides with
the hata axis if all the angular momentum is along the
smallest moment of inertia. Without actually solving the Lagrange
equations, we have found strong constraints on the evolution of the
components of the angular momentum on the principal axes.
To determine how the system evolves along these intersection curves we have to use the equations of motion. We observe that the evolution of the components of the angular momentum on the principal axes depends only on the components of the angular momentum on the principal axes, even though the values of these components are not enough to completely specify the dynamical state. Apparently the dynamics of these components is self-contained, and we will see that it can be described in terms of a set of differential equations whose only dynamical variables are the components of the angular momentum on the principal axes (see section 2.12).
We note that there are two axes for which the intersection curves shrink to a point if we hold the energy constant and vary the magnitude of the angular momentum. If the angular momentum starts at these points, the integrals constrain the angular momentum to stay there. These points are equilibrium points for the body components of the angular momentum. However, they are not equilibrium points for the system as a whole. At these points the body is still rotating even though the body components of the angular momentum are not changing. This kind of equilibrium is called a relative equilibrium. We can also see that if the angular momentum is initially slightly displaced from one of these relative equilibria, then the angular momentum is constrained to stay near it on one of the intersection curves. The angular momentum vector is fixed in space, so the principal axis of the equilibrium point of the body rotates stably about the angular momentum vector.
At the principal axis with intermediate
moment of inertia, the 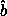 axis, the intersection curves cross.
As we observed, the dynamics of the components of the angular momentum
on the principal axes forms a self-contained dynamical system.
Trajectories of a dynamical system cannot cross,10 so the
most that can happen is that if the equations of motion carry the
system along the intersection curve then the system can approach the crossing point only
asymptotically. So without solving any
equations we can deduce that the point of crossing is another relative
equilibrium. If the angular momentum is initially aligned with the
intermediate axis, then it stays aligned. If the system is slightly
displaced from the intermediate axis, then the evolution along the
intersection curve will take the system far from the relative
equilibrium. So rotation about the axis of intermediate moment of
inertia is unstable -- initial displacements of the angular momentum,
however small initially, become large. Again, the angular momentum
vector is fixed in space, but now the principal axis with the
intermediate principal moment does not stay close to the angular
momentum, so the body executes a complicated tumbling motion.
axis, the intersection curves cross.
As we observed, the dynamics of the components of the angular momentum
on the principal axes forms a self-contained dynamical system.
Trajectories of a dynamical system cannot cross,10 so the
most that can happen is that if the equations of motion carry the
system along the intersection curve then the system can approach the crossing point only
asymptotically. So without solving any
equations we can deduce that the point of crossing is another relative
equilibrium. If the angular momentum is initially aligned with the
intermediate axis, then it stays aligned. If the system is slightly
displaced from the intermediate axis, then the evolution along the
intersection curve will take the system far from the relative
equilibrium. So rotation about the axis of intermediate moment of
inertia is unstable -- initial displacements of the angular momentum,
however small initially, become large. Again, the angular momentum
vector is fixed in space, but now the principal axis with the
intermediate principal moment does not stay close to the angular
momentum, so the body executes a complicated tumbling motion.
This gives some insight into the mystery of the thrown book mentioned at the beginning of the chapter. If one throws a book so that it is initially rotating about either the axis with the largest moment of inertia or the axis with the smallest moment of inertia (the smallest and largest physical axes, respectively), the book rotates regularly about that axis. However, if the book is thrown so that it is initially rotating about the axis of intermediate moment of inertia (the intermediate physical axis), then it tumbles, however carefully it is thrown. You can try it with this book (but put a rubber band or string around it first).
Before moving on, we can make some further physical deductions. Suppose a freely rotating body is subject to some sort of internal friction that dissipates energy but conserves the angular momentum. For example, real bodies flex as they spin. If the spin axis moves with respect to the body then the flexing changes with time, and this changing distortion converts kinetic energy of rotation into heat. Internal processes do not change the total angular momentum of the system. If we hold the magnitude of the angular momentum fixed but gradually decrease the energy, then the curve of intersection on which the system moves gradually deforms. For a given angular momentum there is a lower limit on the energy: the energy cannot be so low that there are no intersections. For this lowest energy the intersection of the angular momentum sphere and the energy ellipsoid is a pair of points on the axis of maximum moment of inertia. With energy dissipation, a freely rotating physical body eventually ends up with the lowest energy consistent with the given angular momentum, which is rotation about the principal axis with the largest moment of inertia (typically the shortest physical axis).
Thus, we expect that given enough time all freely rotating physical
bodies will end up rotating about the axis of largest moment of
inertia. You can demonstrate this to your satisfaction by twirling a
small bottle containing some viscous fluid, such as correction fluid.
What you will find is that, whatever spin you try to put on the
bottle, it will reorient itself so that the axis of the largest moment
of inertia is aligned with the spin axis. Remarkably, this is very
nearly true of almost every body in the solar system for which there
is enough information to decide. The deviations from principal axis
rotation for the Earth are tiny: the angle between the angular
momentum vector and the 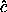 axis for the Earth is less than one
arc-second.11 In fact, the evidence is
that all of the planets, the
Moon and all the other natural satellites,
and almost all of the asteroids rotate
very nearly about the largest moment of inertia. We have deduced that
this is to be expected using an elementary argument. There are
exceptions. Comets typically do not
rotate about the largest moment. As they are heated by the sun,
material spews out from localized jets, and the back reaction from
these jets changes the rotation state. Among the natural satellites,
the only known exception is Saturn's satellite
Hyperion, which is tumbling chaotically. Hyperion is
especially out of round and subject to strong gravitational torques
from Saturn.
axis for the Earth is less than one
arc-second.11 In fact, the evidence is
that all of the planets, the
Moon and all the other natural satellites,
and almost all of the asteroids rotate
very nearly about the largest moment of inertia. We have deduced that
this is to be expected using an elementary argument. There are
exceptions. Comets typically do not
rotate about the largest moment. As they are heated by the sun,
material spews out from localized jets, and the back reaction from
these jets changes the rotation state. Among the natural satellites,
the only known exception is Saturn's satellite
Hyperion, which is tumbling chaotically. Hyperion is
especially out of round and subject to strong gravitational torques
from Saturn.
9 We expect that for each constant of the motion we reduce by one the dimension of the region of the state space explored by a trajectory. This is because a constant of the motion can be used locally to solve for one of the state variables in terms of the others.
10 Systems of ODEs that satisfy a Lipschitz condition have unique solutions.
11 The deviation of the angular momentum from the principal axis may be due to a number of effects: earthquakes, atmospheric tides, ... .