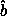 ,
, 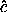 are
coincident with the basis vectors
are
coincident with the basis vectors 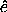 i, labeled here by
i, labeled here by 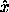 ,
, 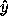 ,
,
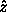 .
. To go further we must finally specify a set of generalized coordinates. We first do this using the traditional Euler angles. Later, we find other ways of describing the orientation of a rigid body.
We are using an intermediate representation of the orientation in
terms of the function M of the generalized coordinates
that gives the rotation that takes the body from some reference
orientation and rotates it to the orientation specified by the
generalized coordinates. Here we take the reference orientation so that
principal-axis unit vectors hata, 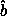 ,
, 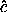 are
coincident with the basis vectors
are
coincident with the basis vectors 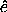 i, labeled here by
i, labeled here by 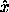 ,
, 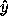 ,
,
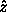 .
.
We define the Euler angles in terms of simple rotations about the
coordinate axes. Let Rx(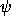 ) be a right-handed rotation about
the
) be a right-handed rotation about
the 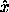 axis by the angle
axis by the angle 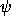 , and let Rz(
, and let Rz(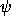 ) be a
right-handed rotation about the
) be a
right-handed rotation about the 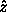 axis by the angle
axis by the angle 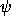 .
The function M for Euler angles is written as a composition
of three of these simple coordinate axis rotations:
.
The function M for Euler angles is written as a composition
of three of these simple coordinate axis rotations:

for the Euler angles 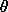 ,
, 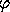 ,
, 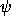 .
.
The Euler angles can specify any orientation of the body, but the
orientation does not always correspond to a unique set of Euler
angles. In particular, if 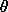 = 0 then the orientation is
dependent only on the sum
= 0 then the orientation is
dependent only on the sum 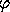 +
+ 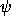 , so the orientation does not
uniquely determine either
, so the orientation does not
uniquely determine either 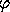 or
or 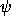 .
.
Exercise 2.8. Euler angles
It is not immediately obvious that all orientations can be represented
in terms of the Euler angles. To show that the Euler angles are adequate
to represent all orientations, solve for the Euler angles that give an
arbitrary rotation R. Keep in mind that some orientations do not
correspond to a unique representation in terms of Euler angles.
Though the Euler angles allow us to specify all orientations and thus can be used as generalized coordinates, the definition of Euler angles is pretty arbitrary. In fact no reasoning has led us to them. This is reflected in our presentation of them by just saying ``here they are.'' Euler angles are well suited for some problems, but cumbersome for others.
There are other ways of defining similar sets of angles. For instance, we could also take our generalized coordinates to satisfy

Such alternatives to the Euler angles come in handy from time to time.
Each of the fundamental rotations can be represented as a matrix.
The rotation matrix representing a right-handed rotation about the
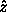 axis by the angle
axis by the angle 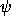 is
is

and a right-handed rotation about the x axis by the angle 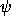 is
represented by the matrix
is
represented by the matrix
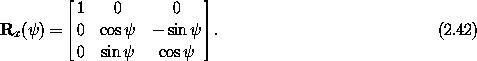
The matrix that represents the rotation that carries the body from its reference orientation to the actual orientation is

The rotation matrices and their product can be constructed by simple programs:
(define (rotate-z-matrix angle)
(matrix-by-rows
(list (cos angle) (- (sin angle)) 0)
(list (sin angle) (cos angle) 0)
(list 0 0 1)))
(define (rotate-x-matrix angle)
(matrix-by-rows
(list 1 0 0)
(list 0 (cos angle) (- (sin angle)))
(list 0 (sin angle) (cos angle))))
(define (Euler->M angles)
(let ((theta (ref angles 0))
(phi (ref angles 1))
(psi (ref angles 2)))
(* (rotate-z-matrix phi)
(rotate-x-matrix theta)
(rotate-z-matrix psi))))
Now that we have a procedure that implements a sample M, we can find the components of the angular velocity vector and the body components of the angular velocity vector using the procedures M-of-q->omega-of-t and M-of-q->omega-body-of-t from section 2.6. For example,
(show-expression
(((M-of-q->omega-body-of-t Euler->M)
(up (literal-function 'theta)
(literal-function 'phi)
(literal-function 'psi)))
't))
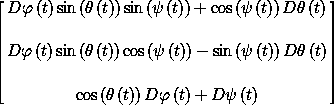
To construct the kinetic energy we need the procedure of state that gives the body components of the angular velocity vector:
(show-expression
((M->omega-body Euler->M)
(up 't
(up 'theta 'phi 'psi)
(up 'thetadot 'phidot 'psidot))))
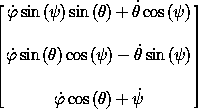
We capture this result as a procedure:
(define (Euler-state->omega-body local)
(let ((q (coordinate local)) (qdot (velocity local)))
(let ((theta (ref q 0))
(psi (ref q 2))
(thetadot (ref qdot 0))
(phidot (ref qdot 1))
(psidot (ref qdot 2)))
(let ((omega-a (+ (* thetadot (cos psi))
(* phidot (sin theta) (sin psi))))
(omega-b (+ (* -1 thetadot (sin psi))
(* phidot (sin theta) (cos psi))))
(omega-c (+ (* phidot (cos theta)) psidot)))
(column-matrix omega-a omega-b omega-c)))))
The kinetic energy can be written:
(define ((T-rigid-body A B C) local)
(let ((omega-body (Euler-state->omega-body local)))
(* 1/2
(+ (* A (square (ref omega-body 0)))
(* B (square (ref omega-body 1)))
(* C (square (ref omega-body 2)))))))