
The vector angular momentum of a particle is the cross product of the position and the linear momentum. For a rigid body the vector angular momentum is the sum of the vector angular momentum of each of the constituents. Here we find an expression for the vector angular momentum of a rigid body in terms of the inertia tensor and the angular velocity vector.
The vector angular momentum of a rigid body is

where 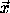
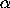 ,
, 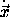
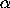 , and m
, and m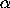 are the positions,
velocities, and masses of the constituent particles.
It turns out that the vector angular momentum decomposes into the sum
of the angular momentum of the center of mass and the rotational
angular momentum about the center of mass, just as the kinetic energy
separates into the
kinetic energy of the center of mass and the kinetic energy of
rotation. As in the kinetic energy demonstration, decompose the
position into the vector to the center of mass
are the positions,
velocities, and masses of the constituent particles.
It turns out that the vector angular momentum decomposes into the sum
of the angular momentum of the center of mass and the rotational
angular momentum about the center of mass, just as the kinetic energy
separates into the
kinetic energy of the center of mass and the kinetic energy of
rotation. As in the kinetic energy demonstration, decompose the
position into the vector to the center of mass 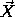 and the
vectors from the center of mass to the constituent mass elements
and the
vectors from the center of mass to the constituent mass elements
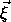
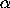 :
:


Substituting, the angular momentum is

Multiplying out the product, and using the fact that 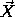 is the
center of mass and M = sum
is the
center of mass and M = sum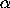 m
m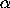 is the total mass of
the body, the angular momentum is
is the total mass of
the body, the angular momentum is

The angular momentum of the center of mass is

and the rotational angular momentum is

We can also reexpress the rotational angular momentum in terms of the
angular velocity vector and the inertia tensor, as we did for the kinetic
energy. Using 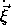
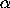 =
= 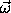 ×
× 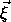
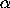 ,
we get the rotational angular momentum
,
we get the rotational angular momentum

In terms of components with respect to the basis {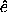 0,
0, 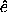 1,
1, 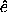 2}, this is
2}, this is

where Ijk are the components of the inertia tensor (2.14). The angular momentum and the kinetic energy are expressed in terms of the same inertia tensor.
With respect to the principal-axis basis, the angular momentum components have a particularly simple form:

Exercise 2.9.
Verify that expression (2.52) for the
components of the rotational angular momentum (2.51)
in terms of the inertia tensor is correct.
We can define procedures to calculate the components of the angular momentum on the principal axes:
(define ((Euler-state->L-body A B C) local)
(let ((omega-body (Euler-state->omega-body local)))
(column-matrix (* A (ref omega-body 0))
(* B (ref omega-body 1))
(* C (ref omega-body 2)))))
We then transform the components of the angular momentum
on the principal axes to the components on the fixed basis
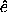 i:
i:
(define ((Euler-state->L-space A B C) local)
(let ((angles (coordinate local)))
(* (Euler->M angles)
((Euler-state->L-body A B C) local))))
These procedures are local state functions, like Lagrangians.