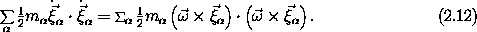
The rotational kinetic energy is the sum of the kinetic energy of each of the constituents of the rigid body. We can rewrite the rotational kinetic energy in terms of the angular velocity vector and certain aggregate quantities determined by the distribution of mass in the rigid body.
Substituting our representation of the relative velocity vectors into the rotational kinetic energy, we obtain
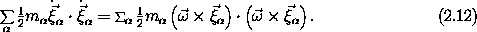
We introduce an arbitrary rectangular coordinate system with origin at
the center of rotation and with basis
vectors 
0, 1, and 2, with the property
that 0 × 1 = 2. The components of
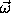on this coordinate system are 
0, 1,
and 2. Rewriting
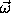in terms of its components, the rotational kinetic
energy becomes
The quantities Iij are the components of the inertia tensor with respect to the chosen coordinate system.
Note what a remarkable form the kinetic energy has taken. All we have done is interchange the order of summations, but now the kinetic energy is written as a sum of products of components of the angular velocity vector, which completely specify how the orientation of the body is changing, and the quantity Iij, which depends solely on the distribution of mass in the body relative to the chosen coordinate system.
We will deduce a number of properties of the inertia tensor. First,
we find a somewhat simpler expression for it. The components of the
vector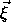 
are ( 
, 
,
).3
If we rewrite 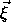as a sum over
its components and simplify the elementary vector products of basis
vectors, we can obtain the components of the inertia tensor.
We can arrange the components of the inertia tensor to form the
inertia matrix I, which looks like:
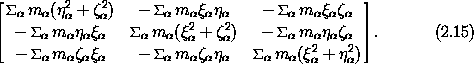
The inertia tensor has real components and is symmetric: Ijk = Ikj.
We define the moment of inertia I about a line by
where | is the perpendicular distance from the line
to the constituent with index . The diagonal components of the
inertia tensor Iii are recognized as the moments of inertia about the
lines coinciding with the coordinate axes i. The off-diagonal
components of the inertia tensor are called products of inertia.
The rotational kinetic energy of a body depends on the distribution of mass of the body solely through the inertia tensor. Remarkably, the inertia tensor involves only second-order moments of the mass distribution with respect to the center of mass. We might have expected the kinetic energy to depend in a complicated way on all the moments of the mass distribution, interwoven in some complicated way with the components of the angular velocity vector, but this is not the case. This fact has a remarkable consequence: for the motion of a free rigid body the detailed shape of the body does not matter. If a book and a banana have the same inertia tensor, that is, the same second-order mass moments, then if they are thrown in the same way the subsequent motion will be the same, however complicated that motion is. The fact that the book has corners and the banana has a stem do not affect the motion except for their contributions to the inertia tensor. In general, the potential energy of an extended body is not so simple and does indeed depend on all moments of the mass distribution, but for the kinetic energy the second moments are all that matter!
Exercise 2.1. Rotational kinetic energy
Show that the
rotational kinetic energy can also be written
where I is the moment of inertia about the line through the center
of mass with direction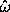 
, and is the
instantaneous rate of rotation.
Exercise 2.2. Steiner's theorem
Let I be the moment of inertia of a body with respect to some given
line through the center of mass. Show that the moment of inertia I' with
respect to a second line parallel to the first is
where M is the total mass of the body and R is the distance between the lines.
Exercise 2.3. Some useful moments of inertia
Show that the moments of inertia of the following objects are as given:
a. The moment of inertia of a sphere of uniform density with mass M and radius R about any line through the center is (2/5) MR2.
b. The moment of inertia of a spherical shell with mass M and radius R about any line through the center is (2/3)MR2.
c. The moment of inertia of a cylinder of uniform density with mass M and radius R about the axis of the cylinder is (1/2) MR2.
c. The moment of inertia of a thin rod of uniform density per unit length with mass M and length L about an axis perpendicular to the rod through the center of mass is (1/12) ML2.
Exercise 2.4. Jupiter
a. The density of a planet increases toward the center.
Provide an argument that the
moment of inertia of a planet is less than that of a sphere of uniform density of
the same mass and radius.
b. The density as a function of radius inside Jupiter is well approximated by
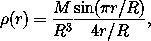
where M is the mass and R is the radius of Jupiter. Find the moment of inertia of Jupiter in terms of M and R.
3 Here we avoid the more consistent notation (0,
1, 2) for the components of
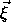
because expressions
involving powers of the components are awkward in this form.