The motion of a rigid body about a center of rotation, a reference
position that is fixed with respect to the body, is characterized at
each moment by a rotation axis and a rate of rotation. Let's
elaborate.
We can get from any orientation of a body to any other orientation of
the body by a rotation of the body. That this is true is called
Euler's theorem on rotations about a point.2
We know that rotations have the property that
they do not commute: the composition of successive rotations in
general depends on the order of operation. Rotating a book about the
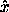 axis and then about the
axis and then about the 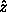 axis puts the book in a
different orientation than rotating the book about the
axis puts the book in a
different orientation than rotating the book about the 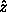 axis
and then about the
axis
and then about the 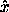 axis. Nevertheless, Euler's theorem
states that however many rotations have been composed to reach a given
orientation, the orientation could have been reached with a single
rotation. Try it! We take a book, rotate it this way, then that, and
then some other way -- then find the rotation that does the job in one
step. So a rotation can be specified by an axis of rotation and the angular
amount of the rotation.
axis. Nevertheless, Euler's theorem
states that however many rotations have been composed to reach a given
orientation, the orientation could have been reached with a single
rotation. Try it! We take a book, rotate it this way, then that, and
then some other way -- then find the rotation that does the job in one
step. So a rotation can be specified by an axis of rotation and the angular
amount of the rotation.
If the orientation of a body evolves over some interval of time, then
the orientation at the beginning and the end of the interval can be
connected by a single rotation. In the limit that the duration of the
interval goes to zero the rotation axis approaches a unique
instantaneous rotation axis. And in this limit the ratio of the
angle of rotation and the duration of the interval approaches
the instantaneous rate of rotation. We represent this instantaneous
rotational motion by the angular velocity vector 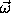 , which
points in the direction of the rotation axis (with the right-hand rule
giving the direction of rotation about the axis) and has a magnitude
equal to the rate of rotation.
, which
points in the direction of the rotation axis (with the right-hand rule
giving the direction of rotation about the axis) and has a magnitude
equal to the rate of rotation.
If the angular velocity vector for a body is 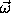 then
the velocities of the constituent particles are perpendicular to the
vectors to the constituent particles and proportional to the
rate of rotation of the body and the distance of the constituent
particle from the instantaneous rotation axis:
then
the velocities of the constituent particles are perpendicular to the
vectors to the constituent particles and proportional to the
rate of rotation of the body and the distance of the constituent
particle from the instantaneous rotation axis:
Isn't it interesting that we have found a concise way of specifying
how the orientation of the body is changing, even though we have not
yet described a way to specify the orientation itself?
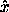 axis and then about the
axis and then about the 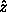 axis puts the book in a
different orientation than rotating the book about the
axis puts the book in a
different orientation than rotating the book about the 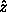 axis
and then about the
axis
and then about the 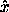 axis. Nevertheless, Euler's theorem
states that however many rotations have been composed to reach a given
orientation, the orientation could have been reached with a single
rotation. Try it! We take a book, rotate it this way, then that, and
then some other way -- then find the rotation that does the job in one
step. So a rotation can be specified by an axis of rotation and the angular
amount of the rotation.
axis. Nevertheless, Euler's theorem
states that however many rotations have been composed to reach a given
orientation, the orientation could have been reached with a single
rotation. Try it! We take a book, rotate it this way, then that, and
then some other way -- then find the rotation that does the job in one
step. So a rotation can be specified by an axis of rotation and the angular
amount of the rotation.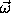 , which
points in the direction of the rotation axis (with the right-hand rule
giving the direction of rotation about the axis) and has a magnitude
equal to the rate of rotation.
, which
points in the direction of the rotation axis (with the right-hand rule
giving the direction of rotation about the axis) and has a magnitude
equal to the rate of rotation. 