 , position
, position

 , and velocities
, and velocities 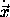
 , with rigid
positional constraints among them. The kinetic energy is
, with rigid
positional constraints among them. The kinetic energy is
We consider a rigid body to be made up of a large number of
constituent particles with mass m , position
, position

 , and velocities
, and velocities 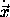
 , with rigid
positional constraints among them. The kinetic energy is
, with rigid
positional constraints among them. The kinetic energy is

It turns out that the kinetic energy of a rigid body can be separated into two pieces: a kinetic energy of translation and a kinetic energy of rotation. Let's see how this comes about.
The configuration of a rigid body is fully specified given the
location of any point in the body and the orientation of the body.
This suggests that it would be useful to decompose the position
vectors for the constituent particles as the sum of the vector
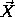 to some reference position in the body and the vector
to some reference position in the body and the vector
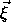
 from the reference position to the particular
constituent element with index
from the reference position to the particular
constituent element with index  :
:

Along paths, the velocities are related by

So in terms of 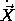 and
and 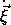
 the kinetic energy is
the kinetic energy is
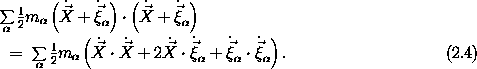
If we select the reference position in the body to be its center of mass,

where M = sum m
m is the total mass of the body, then
is the total mass of the body, then

So along paths the relative velocities satisfy


The kinetic energy is the sum of the kinetic energy of the motion of the total mass at the center of mass

and the kinetic energy of rotation about the center of mass

Written in terms of appropriate generalized coordinates, the kinetic energy is a Lagrangian for a free rigid body. If we choose generalized coordinates so that the center of mass position is entirely specified by some of them and the orientation is entirely specified by others, then the Lagrange equations for a free rigid body will decouple into two groups of equations, one concerned with the motion of the center of mass and one concerned with the orientation.
Such a separation might occur in other problems, such as a rigid body moving in a uniform gravitational field, but in general, potential energies cannot be separated as the kinetic energy separates. So the motion of the center of mass and the rotational motion are usually coupled through the potential. Even in these cases, it is usually an advantage to choose generalized coordinates that separately specify the position of the center of mass and the orientation.