The representation of the rotational kinetic energy in terms of the
inertia tensor was derived with the help of a rectangular coordinate
system with basis vectors  i. There was nothing special
about this particular rectangular basis. So, the kinetic energy must
have the same form in any rectangular coordinate system. We can use
this fact to derive how the inertia tensor changes if the body or the
coordinate system is rotated.
i. There was nothing special
about this particular rectangular basis. So, the kinetic energy must
have the same form in any rectangular coordinate system. We can use
this fact to derive how the inertia tensor changes if the body or the
coordinate system is rotated.
Let's talk a bit about active and passive rotations.
The rotation of the vector  by the rotation R produces a
new vector
by the rotation R produces a
new vector  ' = R
' = R  . We may write
. We may write  in terms of
its components with respect to some arbitrary rectangular coordinate
system with orthonormal basis vectors
in terms of
its components with respect to some arbitrary rectangular coordinate
system with orthonormal basis vectors  i:
i:  = x0
= x0
 0 + x1
0 + x1  1 + x2
1 + x2  2. Let x indicate
the column matrix of components x0, x1, and x2 of
2. Let x indicate
the column matrix of components x0, x1, and x2 of  ,
and R be the matrix representation of R with respect to the
same basis. In these terms the rotation can be written x' = R x. The rotation matrix R is a real orthogonal
matrix.4
A rotation that carries vectors to new vectors is called an active rotation.
,
and R be the matrix representation of R with respect to the
same basis. In these terms the rotation can be written x' = R x. The rotation matrix R is a real orthogonal
matrix.4
A rotation that carries vectors to new vectors is called an active rotation.
Alternately, we can rotate the coordinate system by rotating the basis
vectors, but leave other vectors that might be represented in terms of
them unchanged. If a vector is unchanged but the basis vectors are
rotated, then the components of the vector on the rotated basis vectors
are not the same as the components on the original basis vectors.
Denote the rotated basis vectors by  i' = R
i' = R  i. The
component of a vector along a basis vector is the dot product of the
vector with the basis vector. So the components of the vector
i. The
component of a vector along a basis vector is the dot product of the
vector with the basis vector. So the components of the vector
 along the rotated basis
along the rotated basis  i' are (x')i =
i' are (x')i =  ·
·  i' =
i' =  · (R
· (R  i) = (R-1
i) = (R-1  )
·
)
·  i.5
Thus the components with
respect to the rotated basis elements are the same as the components
of the rotated vector R-1
i.5
Thus the components with
respect to the rotated basis elements are the same as the components
of the rotated vector R-1  with respect to the original
basis. In terms of components, if the vector
with respect to the original
basis. In terms of components, if the vector  has components
x with respect to the original basis vectors
has components
x with respect to the original basis vectors  i, then
the components x' of the same vector with respect to the
rotated basis vectors
i, then
the components x' of the same vector with respect to the
rotated basis vectors  i' are x' = R-1 x, or equivalently x = R x'. A rotation that
actively rotates the basis vectors, leaving other vectors unchanged, is
called a passive rotation. For a passive rotation the
components of a fixed vector change as if the vector was actively
rotated by the inverse rotation.
i' are x' = R-1 x, or equivalently x = R x'. A rotation that
actively rotates the basis vectors, leaving other vectors unchanged, is
called a passive rotation. For a passive rotation the
components of a fixed vector change as if the vector was actively
rotated by the inverse rotation.
With respect to the rectangular basis  i the rotational
kinetic energy is written
i the rotational
kinetic energy is written
In terms of matrix representations, the kinetic energy is
where  is the column of components representing
is the column of components representing
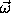 .6
If we rotate the coordinate system by the passive
rotation R about the center of rotation, the new basis vectors are
.6
If we rotate the coordinate system by the passive
rotation R about the center of rotation, the new basis vectors are
 i' = R
i' = R  i. The components
i. The components  ' of the vector
' of the vector
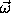 with respect to the rotated coordinate system satisfy
with respect to the rotated coordinate system satisfy
where R is the matrix representation of R.
The kinetic energy is
However, if we had started with the basis  i', we would have
written the kinetic energy directly as
i', we would have
written the kinetic energy directly as
where the components are taken with respect to the  i' basis.
Comparing the two expressions, we see that
i' basis.
Comparing the two expressions, we see that
Thus the inertia matrix transforms by a similarity
transformation.7
 i. There was nothing special
about this particular rectangular basis. So, the kinetic energy must
have the same form in any rectangular coordinate system. We can use
this fact to derive how the inertia tensor changes if the body or the
coordinate system is rotated.
i. There was nothing special
about this particular rectangular basis. So, the kinetic energy must
have the same form in any rectangular coordinate system. We can use
this fact to derive how the inertia tensor changes if the body or the
coordinate system is rotated. by the rotation R produces a
new vector
by the rotation R produces a
new vector 

 is the column of components representing
is the column of components representing
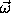 .
.



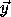 = (R
= (R