2.5  Principal Moments of Inertia

We can use the transformation properties of the inertia tensor (2.24) to show that there are special rectangular coordinate systems for which the inertia tensor I' is diagonal, that is, I'_ij = 0 for i ne j. Let's assume that I' is diagonal and solve for the rotation matrix R that does the job. Multiplying both sides of (2.24) on the left by R, we have

We can examine pieces of this matrix equation by multiplying on the right by a trivial column vector that picks out a particular column. So we multiply on the right by the column matrix representation e_i of each of the coordinate unit vectors _i. These column matrices have a one in the ith row and zeros otherwise. Using e_i' = R e_i, we find

The matrix I' is diagonal so

So, from equations (2.26) and (2.27), we have

which we recognize as an equation for the eigenvalue I'_ii and e_i', the column matrix of components of the associated eigenvector.

From e_i' = R e_i, we see that the e_i' are the columns of the rotation matrix R. Now, rotation matrices are orthogonal, so R^T R = 1; thus the columns of the rotation matrix must be orthonormal -- that is, (e_i')^T e_j' = _ij, where _ij is one if i = j and zero otherwise. But the eigenvectors that are solutions of equation (2.28) are not necessarily even orthogonal. So we are not done yet.

If a matrix is real and symmetric then the eigenvalues are real. Furthermore, if the eigenvalues are distinct then the eigenvectors are orthogonal. However, if the eigenvalues are not distinct then the directions of the eigenvectors for the degenerate eigenvalues are not uniquely determined -- we have the freedom to choose particular e_i' that are orthogonal.⁸ The linearity of equation (2.28) implies the e_i' can be normalized. Thus whether or not the eigenvalues are distinct we can obtain an orthonormal set of e_i. This is enough to reconstruct a rotation matrix R that does the job we asked of it: to rotate the coordinate system to a configuration such that the inertia tensor is diagonal. If the eigenvalues are not distinct, the rotation matrix R is not uniquely defined -- there is more than one rotation matrix R that does the job.

The eigenvectors and eigenvalues are determined by the requirement that the inertia tensor be diagonal with respect to the rotated coordinate system. Thus the rotated coordinate system has a special orientation with respect to the body. The basis vectors _i' therefore actually point along particular directions in the body. We define the axes in the body through the center of mass with these directions to be the principal axes. With respect to the coordinate system defined by _i', the inertia tensor is diagonal, by construction, with the eigenvalues I'_ii on the diagonal. Thus the moments of inertia about the principal axes are the eigenvalues I'_ii. We call the moments of inertia about the principal axes the principal moments of inertia.

For convenience, we often label the principal moments of inertia according to their size: A < B < C, with principal axis unit vectors hata, 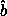, , 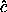respectively. The positive direction along the principal axes can be chosen so that hata, 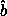, 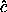form a right-handed rectangular coordinate basis.

Let x represent the matrix of components of a vector with respect to the basis vectors _i. Recall that the components x' of a vector with respect to the principal axis unit vectors _i' satisfy

This makes sense because the columns of R are the components of e_i'. Multiplying the components of by the transpose of R is taking the dot product of each _i' with to produce the components. The components of a vector on the principal axis basis are sometimes called the body components of the vector. Now let's rewrite the kinetic energy in terms of the principal moments of inertia. If we choose our rectangular coordinate system so that it coincides with the principal axes then the calculation is simple. Let the components of the angular velocity vector on the principal axes be ( ^a, ^b, ^c ). Then, keeping in mind that the inertia tensor is diagonal with respect to the principal axis basis, the kinetic energy is just

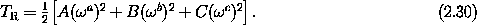
Exercise 2.5.  A constraint on the moments of inertia
Show that the sum of any two of the moments of inertia is greater than or equal to the third moment of inertia. You may assume the moments of inertia are with respect to orthogonal axes.

Exercise 2.6.  Principal moments of inertia
For each of the configurations described below find the principal moments of inertia with respect to the center of mass; find the corresponding principal axes.

a.  A regular tetrahedron consisting of four equal point masses tied together with rigid massless wire.

b.  A cube of uniform density.

c.  Five equal point masses rigidly connected by massless stuff. The point masses are at the rectangular coordinates:

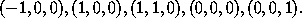
Exercise 2.7.  This book
Measure this book. You will admit that it is pretty dense. Don't worry, you will get to throw it later. Show that the principal axes are the lines connecting the centers of opposite faces of the idealized brick approximating the book. Compute the corresponding principal moments of inertia.