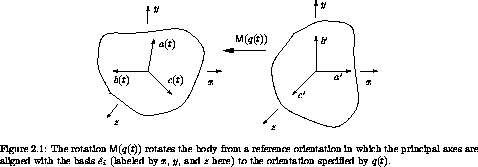
We can specify the orientation of a body by specifying the rotation that takes the body to this orientation from some reference orientation. As the body moves, the rotation that does this changes. The angular velocity vector can be written in terms of this changing rotation along a path.
Let q be the coordinate path that we will use to describe
the motion of the body. Let M(q(t)) be the rotation
that takes the body from the reference orientation to the orientation
specified by q(t) (see figure 2.1). Let
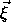
(t) be the vector to some constituent particle with the body
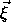
in the orientation specified by q(t), and let ' be
the vector to the same constituent with the body in the reference
orientation.
Then
The constituent vectors
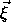
/ do not depend on the configuration, because they
are the vectors to the positions of the constituents with the body in a
fixed reference orientation.
We have already found an expression for the kinetic energy in terms of the angular velocity vector and the inertia tensor. Here we do this in a different way. To compute the kinetic energy we accumulate the contributions from all of the mass elements. The positions of the constituent particles, at a given time t, are
where M = M o q. The velocity is the time derivative
Using equation (2.32), we can write
Recall that the velocity results from a rotation, and that the velocities are (see equation 2.11)
Thus we can identify the operator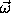 
(t) × with DM(t)
(M(t))-1. To form the kinetic energy we need to extract
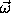(t) from this.
If a vector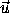 
is represented by the component matrix u with components x, y, and z, the function A
that produces the matrix representation of
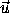× from the component matrix u is
The inverse of this function can
be applied to any skew-symmetric matrix, and so we can use
A-1 to extract the components 
of the angular velocity vector
from the matrix representation of ×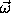
in terms of M:
where M and DM are the matrix representations of the functions M and DM, and where we have used the fact that for a matrix representation of a rotation the transpose gives the inverse.
The components ' of the angular velocity vector on the
principal axes are ' = MT , so
The relationship of the angular velocity vector to the path is a kinematic relationship; it is valid for any path. Thus we can abstract it to obtain the components of the angular velocity at a moment given the configuration and velocity at that moment.
The following procedure gives the components of the angular velocity as a function of time along the path:
(define (((M-of-q->omega-of-t M-of-q) q) t)
(define M-on-path (compose M-of-q q))
(define (omega-cross t)
(* ((D M-on-path) t)
(m:transpose (M-on-path t))))
(antisymmetric->column-matrix (omega-cross t)))
The procedure omega-cross produces the matrix representation of
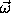×. The procedure antisymmetric->column-matrix, which corresponds to the function
A-1, is used to extract the
components of the angular velocity vector from the skew-symmetric
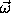× matrix.
The body components of the angular velocity vector as a function of time along the path are
(define (((M-of-q->omega-body-of-t M-of-q) q) t)
(* (m:transpose (M-of-q (q t)))
(((M-of-q->omega-of-t M-of-q) q) t)))
We can get the procedures of local state that give the angular velocity components by abstracting these procedures along arbitrary paths that have given coordinates and velocities. The abstraction of a procedure of a path to a procedure of state is accomplished by Gamma-bar (see section 1.9):
(define (M->omega M-of-q)
(Gamma-bar
(M-of-q->omega-of-t M-of-q)))
(define (M->omega-body M-of-q)
(Gamma-bar
(M-of-q->omega-body-of-t M-of-q)))
These procedures give the angular velocities as a function of state. We will see them in action after we get some M-of-q's with which to work.