An essential step in the derivation of the local-tuple transformation
function C from the coordinate transformation F was the deduction
of the relationship between the velocities in the two coordinate
systems. We did this by inserting coordinate paths into the
coordinate transformation function F, differentiating, and then
generalizing the results on the path to arbitrary velocities at a
moment. The last step is an example of a more general problem of
abstracting a local-tuple function from a path function. Given a
function f of a local tuple, a corresponding path-dependent function
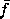 [q] is
[q] is 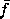 [q] = f o
[q] = f o  [q]. Given
[q]. Given 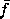 ,
how can we reconstitute f? The local-tuple function f depends on
only a finite number of components of the local tuple, and
,
how can we reconstitute f? The local-tuple function f depends on
only a finite number of components of the local tuple, and 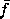 depends only on the corresponding local components of the path. So
depends only on the corresponding local components of the path. So
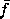 has the same value for all paths that have that number of
components of the local tuple in common. Given
has the same value for all paths that have that number of
components of the local tuple in common. Given 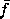 we can
reconstitute f by taking the argument of f, which is a finite
initial segment of a local tuple, constructing a path that has this
local description, and finding the value of
we can
reconstitute f by taking the argument of f, which is a finite
initial segment of a local tuple, constructing a path that has this
local description, and finding the value of 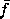 for this path.
for this path.
Two paths that have the same local description up to the nth derivative are said to osculate with order-n contact. For
example, a path and the truncated power series representation of the
path up to order n have order-n contact; if fewer than n
derivatives are needed by a local-tuple function, the path and the
truncated power series representation are equivalent. Let O be a
function that generates an osculating path with the given local-tuple
components. So O(t, q, v, ...)(t) = q,
D(O(t, q, v, ...))(t) = v, and in general
The number of components of the local tuple that are required is
finite, but unspecified.
One way of constructing O is through the truncated power series
where the number of terms is the same as the number of components of
the local tuple that are specified.
Given the path function 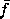 we reconstitute the f function as
follows. We take the argument of f and construct an osculating path
with this local description. Then the value of f is the value of
we reconstitute the f function as
follows. We take the argument of f and construct an osculating path
with this local description. Then the value of f is the value of
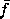 for this osculating path:
for this osculating path:
Let 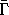 be the function that takes
a path function and returns the corresponding local-tuple function:
be the function that takes
a path function and returns the corresponding local-tuple function:
From equation (1.165) we see that
The procedure Gamma-bar implements the function 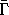 that reconstitutes a path-dependent function into a local-tuple function:
that reconstitutes a path-dependent function into a local-tuple function:
(define ((Gamma-bar f-bar) local)
((f-bar (osculating-path local)) (time local)))
The procedure osculating-path takes a number of local
components and returns a path with these components; it is implemented
as a power series.
We can use Gamma-bar to construct the procedure F->C
that takes a coordinate transformation F and generates the
procedure that transforms local tuples. The procedure F->C
constructs a path-dependent procedure f-bar that takes a
coordinate path in the primed system and returns the local tuple of
the corresponding path in the unprimed coordinate system. It then
uses Gamma-bar to abstract f-bar to arbitrary local
tuples in the primed coordinate system.
(define (F->C F)
(define (f-bar q-prime)
(define q
(compose F (Gamma q-prime)))
(Gamma q))
(Gamma-bar f-bar))
(show-expression
((F->C p->r)
(->local 't (up 'r 'theta) (up 'rdot 'thetadot))))
Notice that in this definition of F->C we do not explicitly calculate any derivatives. The calculation
that led up to the state transformation (1.74) is not
needed.
We can also use 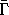 to make an elegant formula for
computing the total time derivative Dt F of the function F:
to make an elegant formula for
computing the total time derivative Dt F of the function F:
The total time derivative can be expressed as a program:
(define (Dt F)
(define (G-bar q)
(D (compose F (Gamma q))))
(Gamma-bar G-bar))
Given a procedure
F implementing a local-tuple function and a path q, we
construct a new procedure (compose F (Gamma q)). The procedure
G-bar implements the derivative of this function of
time. We then abstract this off the path with Gamma-bar to give
the total time derivative.
Exercise 1.31. Velocity transformation
Use the procedure Gamma-bar to construct a procedure that
transforms velocities given a coordinate transformation. Apply this
procedure to the procedure p->r to deduce (again)
equation (1.65).
Exercise 1.32. Path functions and state functions
The local-tuple function f is the same as the local-tuple function
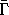 (
(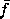 ) where
) where 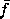 [q] = f o
[q] = f o  [q]. On
the other hand, the path function
[q]. On
the other hand, the path function 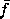 [q] and the path function
[q] and the path function
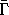 (
(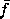 ) o
) o  [q] are not necessarily the same.
Explain. Give examples where they are the same and where they are
not the same. Write programs to illustrate the behavior.
[q] are not necessarily the same.
Explain. Give examples where they are the same and where they are
not the same. Write programs to illustrate the behavior.
Given a Lagrangian, the Lagrange equations test paths to determine whether they
are realizable paths of the system. The Lagrange equations relate the
path and its derivatives. The fact that the Lagrange equations must
be satisfied at each moment suggests that we can abstract the
Lagrange equations off the path and write them as relations among the
local-tuple components of realizable paths.
Let 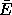 [L] be the path-dependent function that produces the
residuals of the Lagrange equations (1.18) for
the Lagrangian L:
[L] be the path-dependent function that produces the
residuals of the Lagrange equations (1.18) for
the Lagrangian L:
Realizable paths q satisfy the Lagrange equations
The path-dependent Lagrange equations can be converted to local
Lagrange equations using 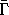 :
:
The operator E is called the Euler-Lagrange operator.
In terms of this operator the Lagrange equations are
Applying the definition (1.167) of 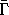 yields
yields
So the Euler-Lagrange operator is explicitly
The procedure Euler-Lagrange-operator implements E:
(define (Euler-Lagrange-operator L)
(- (Dt ((partial 2) L)) ((partial 1) L))) .
For example, applied to the Lagrangian for the harmonic oscillator, we
have
(print-expression
((Euler-Lagrange-operator
(L-harmonic 'm 'k))
(->local 't 'x 'v 'a)))
(+ (* a m) (* k x))
Notice that the components of the local tuple are individually
specified. Using equation (1.172), the
Lagrange equations for the harmonic oscillator are87
(print-expression
((compose
(Euler-Lagrange-operator (L-harmonic 'm 'k))
(Gamma (literal-function 'x) 4))
't))
(+ (* k (x t)) (* m (((expt D 2) x) t)))
Exercise 1.33. Properties of E
Let F and G be two Lagrangian-like functions of a local tuple, C
be a local-tuple transformation function, and c a constant.
Demonstrate the following properties:
a. E[F + G] = E[F] + E[G]
b. E[c F] = c E[F]
c. E[F G] = E[F] G + F E[G] + (Dt F)  2 G +
2 G +
 2 F (Dt G)
2 F (Dt G)
d. E[F o C] = Dt (DF o C)  2 C + DF o C E[C]
2 C + DF o C E[C]
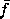 [q] is
[q] is 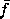 [q] = f o
[q] = f o  [q]. Given
[q]. Given 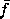 ,
how can we reconstitute f? The local-tuple function f depends on
only a finite number of components of the local tuple, and
,
how can we reconstitute f? The local-tuple function f depends on
only a finite number of components of the local tuple, and 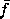 depends only on the corresponding local components of the path. So
depends only on the corresponding local components of the path. So
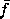 has the same value for all paths that have that number of
components of the local tuple in common. Given
has the same value for all paths that have that number of
components of the local tuple in common. Given 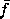 we can
reconstitute f by taking the argument of f, which is a finite
initial segment of a local tuple, constructing a path that has this
local description, and finding the value of
we can
reconstitute f by taking the argument of f, which is a finite
initial segment of a local tuple, constructing a path that has this
local description, and finding the value of 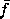 for this path.
for this path.
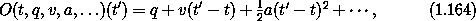
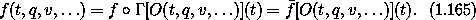
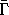 be the function that takes
a path function and returns the corresponding local-tuple function:
be the function that takes
a path function and returns the corresponding local-tuple function:

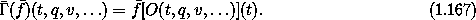
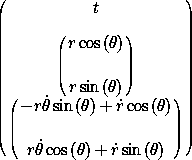
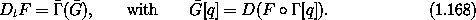
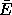 [L] be the path-dependent function that produces the
residuals of the Lagrange equations (
[L] be the path-dependent function that produces the
residuals of the Lagrange equations (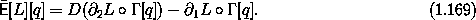



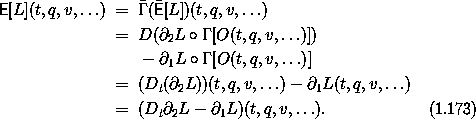

 2 G +
2 G +