
An advantage of the Lagrangian approach is that coordinates can often be chosen that exactly describe the freedom of the system, automatically incorporating any constraints. We may also use coordinates that have more freedom than the system actually has and consider explicit constraints among the coordinates. For example, the planar pendulum has a one-dimensional configuration space. We have formulated this problem using the angle from the vertical as the configuration coordinate. Alternatively, we may choose to represent the pendulum as a body moving in the plane, constrained to be on the circle of the correct radius around the pivot. We would like to have valid descriptions for both choices and show they are equivalent. In this section we develop tools to handle problems with explicit constraints. The constraints considered here are more general than those used in the demonstration that the Lagrangian for systems with rigid constraints can be written as the difference of kinetic and potential energies (see section 1.6.2).
Suppose the configuration of a system with n degrees of freedom is specified by n + 1 coordinates and that configuration paths q are constrained to satisfy some relation of the form

How do we formulate the equations of motion? One approach would be to use the constraint equation to eliminate one of the coordinates in favor of the rest; then the evolution of the reduced set of generalized coordinates would be described by the usual Lagrange equations. The equations governing the evolution of coordinates that are not fully independent should be equivalent.
We can address the problem of formulating equations of motion for systems with redundant coordinates by returning to the action principle. Realizable paths are distinguished from other paths by having stationary action. Stationary refers to the fact that the action does not change with certain small variations of the path. What variations should be considered? We have seen that velocity-independent rigid constraints can be used to eliminate redundant coordinates. In the irredundant coordinates we distinguished realizable paths by using variations that by construction satisfy the constraints. Thus in the case where constraints can be used to eliminate redundant coordinates we can restrict the variations in the path to those that are consistent with the constraints.
So how does the restriction of the possible variations affect the argument that led to Lagrange's equations (refer to section 1.5)? Actually most of the calculation is unaffected. The condition that the action is stationary still reduces to the condition (1.34):
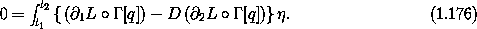
At this point we argued that because the variations  are
arbitrary (except for conditions at the endpoints), the only way for
the integral to be zero is for the integrand to be zero. Furthermore,
the freedom in our choice of
are
arbitrary (except for conditions at the endpoints), the only way for
the integral to be zero is for the integrand to be zero. Furthermore,
the freedom in our choice of  allowed us to deduce that the factor
multiplying
allowed us to deduce that the factor
multiplying  in the integrand must be identically zero, thereby
deriving Lagrange's equations.
in the integrand must be identically zero, thereby
deriving Lagrange's equations.
Now the choice of  is not completely free. We can still deduce
from the arbitrariness of
is not completely free. We can still deduce
from the arbitrariness of  that the integrand must be zero,88
but we can no longer deduce that the factor
multiplying
that the integrand must be zero,88
but we can no longer deduce that the factor
multiplying  is zero (only that the projection of this factor
onto acceptable variations is zero). So we have
is zero (only that the projection of this factor
onto acceptable variations is zero). So we have
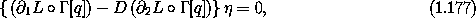
with  subject to the constraints.
subject to the constraints.
A path q satisfies the constraint if 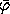 [q]
=
[q]
=  o
o  [q] = 0. The constraint must be satisfied even
for the varied path, so we allow only variations
[q] = 0. The constraint must be satisfied even
for the varied path, so we allow only variations  for which the
variation of the constraint is zero:
for which the
variation of the constraint is zero:

We can say that the variation must be ``tangent'' to the constraint
surface.
Expanding this with the chain rule, a variation  is tangent to the
constraint surface
is tangent to the
constraint surface  if
if
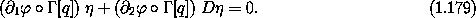
Note that these are functions of time; the variation at a given time is tangent to the constraint at that time.
Consider constraints that do not depend on velocities:
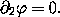
In this case the variation is tangent to the constraint surface if

Together, equations (1.177) and
(1.180) should determine the motion, but how do
we eliminate  ? The residual of the Lagrange
equations is orthogonal89
to any
? The residual of the Lagrange
equations is orthogonal89
to any  that is orthogonal to the
normal to the constraint surface. A vector that is orthogonal to
all vectors orthogonal to a given vector is parallel to the given
vector. Thus, the residual of Lagrange's equations is parallel to the
normal to the constraint surface; the two must be proportional:
that is orthogonal to the
normal to the constraint surface. A vector that is orthogonal to
all vectors orthogonal to a given vector is parallel to the given
vector. Thus, the residual of Lagrange's equations is parallel to the
normal to the constraint surface; the two must be proportional:
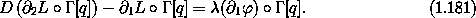
That the two vectors are parallel everywhere along the path does not
guarantee that the proportionality factor is the same at each moment
along the path, so the proportionality factor  is some
function of time, which may depend on the path under consideration.
These equations, with the constraint equation
is some
function of time, which may depend on the path under consideration.
These equations, with the constraint equation  o
o  [q]
= 0, are the governing equations. These equations are sufficient to
determine the path q and to eliminate the unknown function
[q]
= 0, are the governing equations. These equations are sufficient to
determine the path q and to eliminate the unknown function
 .
.
Suppose we form an augmented Lagrangian treating
 as one of the coordinates:
as one of the coordinates:
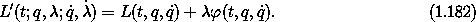
The Lagrange equations associated with the coordinates q are just
the modified Lagrange
equations (1.181),
and the Lagrange equation associated with  is just the
constraint equation. (Note that
is just the
constraint equation. (Note that 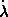 does not appear in
the augmented Lagrangian.) So the Lagrange equations for this augmented
Lagrangian fully encapsulate the modification to the Lagrange
equations that is imposed by the addition of an explicit coordinate
constraint, at the expense of introducing extra degrees of freedom.
Notice that this Lagrangian is of the same form as
the Lagrangian (equation 1.89) that we used in the
derivation of L = T - V for rigid systems
(section 1.6.2).
does not appear in
the augmented Lagrangian.) So the Lagrange equations for this augmented
Lagrangian fully encapsulate the modification to the Lagrange
equations that is imposed by the addition of an explicit coordinate
constraint, at the expense of introducing extra degrees of freedom.
Notice that this Lagrangian is of the same form as
the Lagrangian (equation 1.89) that we used in the
derivation of L = T - V for rigid systems
(section 1.6.2).
How do we know that we have enough information to eliminate the
unknown function  from
equations (1.181), or
that the extra degree of freedom introduced in
Lagrangian (1.182) is purely formal?
from
equations (1.181), or
that the extra degree of freedom introduced in
Lagrangian (1.182) is purely formal?
If  could be written as a function of the solution
state path, then it would be clear that it is determined by the state
and can thus be eliminated. Suppose
could be written as a function of the solution
state path, then it would be clear that it is determined by the state
and can thus be eliminated. Suppose  can be written as a
composition of a state-dependent function with the path:
can be written as a
composition of a state-dependent function with the path:  =
= 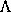 o
o  [q]. Consider the Lagrangian
[q]. Consider the Lagrangian

This new Lagrangian has no extra degrees of freedom.
The Lagrange equations for L'' are the Lagrange equations for L
with additional terms arising from the product of 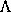
 .
Applying the Euler-Lagrange operator E (see
section 1.9) to this Lagrangian gives90
.
Applying the Euler-Lagrange operator E (see
section 1.9) to this Lagrangian gives90
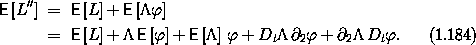
Composition of E[L''] with  [q] gives the Lagrange
equations for the path q. Using the fact that
the constraint is satisfied on the path
[q] gives the Lagrange
equations for the path q. Using the fact that
the constraint is satisfied on the path
 o
o  [q] = 0 and consequently
Dt
[q] = 0 and consequently
Dt  o
o  [q] = 0,
we have
[q] = 0,
we have
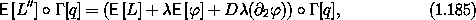
where we have used  =
= 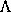 o
o  [q].
If we now use the fact that we are dealing only with coordinate
constraints,
[q].
If we now use the fact that we are dealing only with coordinate
constraints,  2
2  = 0, then
= 0, then
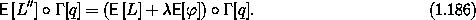
The Lagrange equations are the same as those derived from
the augmented Lagrangian L'. The difference is that now we see that
 =
= 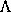 o
o  [q] is determined by the unaugmented state.
This is the same as saying that
[q] is determined by the unaugmented state.
This is the same as saying that  can be eliminated.
can be eliminated.
Considering only the formal validity of the Lagrange equations for the
augmented Lagrangian, we could not deduce that  could
be written as the composition of a state-dependent function
could
be written as the composition of a state-dependent function 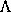 with
with  [q]. The explicit Lagrange equations derived from the
augmented Lagrangian depend on the accelerations D2q as well as
[q]. The explicit Lagrange equations derived from the
augmented Lagrangian depend on the accelerations D2q as well as
 , so we cannot deduce separately that either is the
composition of a state-dependent function and
, so we cannot deduce separately that either is the
composition of a state-dependent function and  [q]. However, now
we see that
[q]. However, now
we see that  is such a composition. This allows us to
deduce that D2q is also a state-dependent function composed
with the path. The evolution of the system is determined from the
dynamical state.
is such a composition. This allows us to
deduce that D2q is also a state-dependent function composed
with the path. The evolution of the system is determined from the
dynamical state.
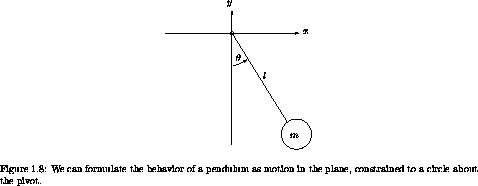
The pendulum can be formulated as the motion of a massive particle in a vertical plane subject to the constraint that the distance to the pivot is constant (see figure 1.8).
In this formulation, the kinetic and potential energies in the Lagrangian are those of an unconstrained particle in a uniform gravitational acceleration. A Lagrangian for the unconstrained particle is
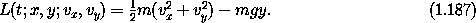
The constraint that the pendulum moves in a circle of radius l about the pivot is91

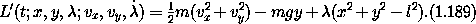
The Lagrange equations for the augmented Lagrangian are

These equations are sufficient to solve for the motion of the pendulum.
It should not be surprising that these equations simplify if we switch to ``polar'' coordinates

Substituting this into the constraint equation, we determine that r = l, a constant. Forming the derivatives and substituting into the other two equations, we find
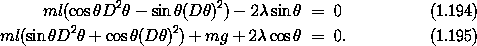
Multiplying the first by cos  and the second by sin
and the second by sin  and adding, we find
and adding, we find

which we recognize as the correct equation for the pendulum. This is
the same as the Lagrange equation for the pendulum using the
unconstrained generalized coordinate  . For completeness, we
can find
. For completeness, we
can find  in terms of the other variables:
in terms of the other variables:
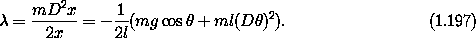
This confirms that  is really the composition of a function
of the state with the state path. Notice that 2 l
is really the composition of a function
of the state with the state path. Notice that 2 l  is a
force -- it is the sum of the outward component of the gravitational
force and the centrifugal force. Using this interpretation in the two
coordinate equations of motion, we see that the terms involving
is a
force -- it is the sum of the outward component of the gravitational
force and the centrifugal force. Using this interpretation in the two
coordinate equations of motion, we see that the terms involving
 are the forces that must be applied to the unconstrained
particle to make it move on the circle required by the constraints.
Equivalently, we may think of 2 l
are the forces that must be applied to the unconstrained
particle to make it move on the circle required by the constraints.
Equivalently, we may think of 2 l  as the tension in the
pendulum rod that holds the mass.92
as the tension in the
pendulum rod that holds the mass.92
The method of using augmented Lagrangians to enforce constraints on dynamical systems provides a way to analyze a compound system by combining the results of the analysis of the parts of the system and the coupling between them.
Consider the compound spring-mass system shown at the top of figure 1.9. We could analyze this as a monolithic system with two configuration coordinates x1 and x2, representing the extensions of the springs from their equilibrium lengths X1 and X2.
An alternative procedure is to break the system into several parts.
In our spring-mass system we can choose two parts: one is a spring and
mass attached to the wall, and the other is a spring and mass with its
attachment point at an additional configuration coordinate  . We
can formulate a Lagrangian for each part separately. We can then
choose a Lagrangian for the composite system as the sum of the two
component Lagrangians with a constraint
. We
can formulate a Lagrangian for each part separately. We can then
choose a Lagrangian for the composite system as the sum of the two
component Lagrangians with a constraint  = X1 + x1 to
accomplish the coupling.
= X1 + x1 to
accomplish the coupling.
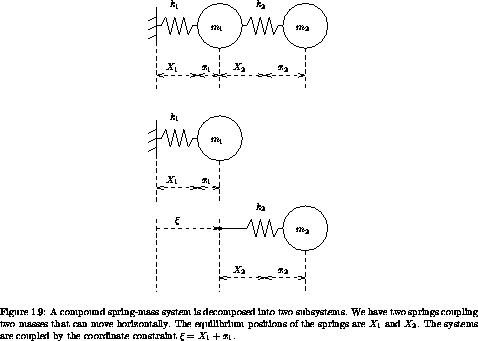
Let's see how this works. The Lagrangian for the subsystem attached to the wall is

and the Lagrangian for the subsystem that attaches to it is
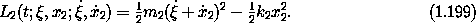
We construct a Lagrangian for the system composed from these parts as a sum of the Lagrangians for each of the separate parts, with a coupling term to enforce the constraint:
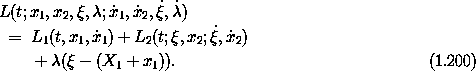
Thus we can write Lagrange's equations for the four configuration coordinates, in order, as follows:
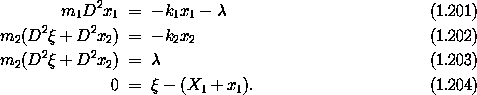
Notice that in this system  is the force of
constraint holding the system together.
We can now eliminate the ``glue'' coordinates
is the force of
constraint holding the system together.
We can now eliminate the ``glue'' coordinates  and
and
 to obtain the equations of
motion in the coordinates x1 and x2:
to obtain the equations of
motion in the coordinates x1 and x2:
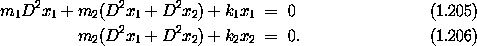
This strategy can be generalized. We can make a library of primitive components. Each component may be characterized by a Lagrangian with additional degrees of freedom for the terminals where that component may be attached to others. We then can construct composite Lagrangians by combining components, using constraints to glue together the terminals.
Exercise 1.34. Combining Lagrangians
a. Make another primitive component, compatible with the
spring-mass structures described in this section. For example, make a
pendulum that can attach to the spring-mass system. Build a
combination and derive the equations of motion. Be careful, the
algebra is horrible if you choose bad coordinates.
b. For a nice little project, construct a family of compatible mechanical parts, characterized by appropriate Lagrangians, that can be combined in a variety of ways to make interesting mechanisms. Remember that in a good language the result of combining pieces should be a piece of the same kind that can be further combined with other pieces.
Exercise 1.35. Bead on a triaxial surface
Consider again the motion of a bead constrained to move on a triaxial
surface (exercise 1.18). Reformulate
this using rectangular coordinates as the generalized coordinates with
an explicit constraint that the bead stay on the surface. Find
a Lagrangian and show that the Lagrange equations are equivalent to
those found in exercise 1.18.
Exercise 1.36. Motion of a tiny golf ball
Consider the motion of a golf ball idealized as a point mass
constrained to a frictionless smooth surface of varying height h(x,
y) in a uniform gravitational field with acceleration g.
a. Find an augmented Lagrangian for this system, and derive the equations governing the motion of the point mass in x and y.
b. Under what conditions is this approximated by a potential function V(x, y) = mgh(x, y)?
c. Assume that h(x, y) is axisymmetric about x = y = 0. Can you find such an h that yields motions with closed orbits?
Here we investigate velocity-dependent constraints that are ``total time derivatives'' of velocity-independent constraints. The methods presented so far do not apply because the constraint is velocity-dependent.
Consider a velocity-dependent constraint  = 0.
That
= 0.
That  is a total time derivative means that there exists a
velocity-independent function
is a total time derivative means that there exists a
velocity-independent function  such that
such that

That  is velocity-independent means
is velocity-independent means  2
2  = 0.
As state functions the relationship between
= 0.
As state functions the relationship between  and
and  is
is

Given a  we can find
we can find  by solving this linear partial
differential equation. The solution is determined up to a constant,
so
by solving this linear partial
differential equation. The solution is determined up to a constant,
so  = 0 implies
= 0 implies  = K for some constant K. On the other
hand, if we knew
= K for some constant K. On the other
hand, if we knew  = K then
= K then  = 0 follows. Thus the
velocity-dependent constraint
= 0 follows. Thus the
velocity-dependent constraint  = 0 is equivalent to the
velocity-independent constraint
= 0 is equivalent to the
velocity-independent constraint  = K, and we know how to find
Lagrange equations for such systems.
= K, and we know how to find
Lagrange equations for such systems.
If L is a Lagrangian for the unconstrained problem, the Lagrange
equations with the constraint  = K are
= K are

where  is a function of time that will be eliminated during the
solution process. The constant K does not affect the Lagrange
equations. The function
is a function of time that will be eliminated during the
solution process. The constant K does not affect the Lagrange
equations. The function  is independent of velocity,
is independent of velocity,  2
2
 = 0, so the Lagrange equations become
= 0, so the Lagrange equations become

From equation (1.208) we see that

so the Lagrange equations with the constraint  = 0 are
= 0 are

The important feature is that we can write the Lagrange equations
directly in terms of  without having to produce the integral
without having to produce the integral
 . But the validity of these Lagrange equations depends on
the existence of the integral
. But the validity of these Lagrange equations depends on
the existence of the integral  .
.
It turns out that the augmented Lagrangian trick also works here.
These Lagrange equations are given if we augment the Lagrangian with
the constraint  multiplied by a function of time
multiplied by a function of time  ':
':

The Lagrange equations for L' turn out to be

which,
with the identification  = - D
= - D ', are the same as
Lagrange equations (1.212).
', are the same as
Lagrange equations (1.212).
Sometimes a problem can be naturally formulated in terms of velocity-dependent constraints. The formalism we have developed will handle any velocity-dependent constraint that can be written in terms of the derivative of a coordinate constraint. Such a constraint is called an integrable constraint. Any system for which the constraints can be put in the form of a coordinate constraint, or are already in that form, is called a holonomic system.
Exercise 1.37.
Show that the augmented
Lagrangian (1.213) does lead to the
Lagrange
equations (1.214), taking
into account the fact that  is a total time derivative of
is a total time derivative of  .
.
Here we consider a problem for which the constraint can be represented as a time derivative of a coordinate constraint: a hoop of mass M rolling, without slipping, down a (one-dimensional) inclined plane (see figure 1.10).93
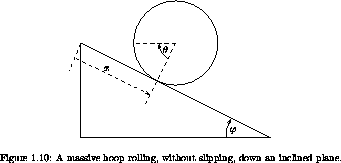
We will formulate this problem in terms of the two
coordinates  ,
the rotation of an arbitrary point on the hoop from an
arbitrary reference direction, and x, the linear progress down the
inclined plane. The constraint is that the hoop does not slip.
Thus a change in
,
the rotation of an arbitrary point on the hoop from an
arbitrary reference direction, and x, the linear progress down the
inclined plane. The constraint is that the hoop does not slip.
Thus a change in  is exactly reflected in a change in x;
the constraint function is
is exactly reflected in a change in x;
the constraint function is

This constraint is phrased as a relation among generalized velocities, but it
could be integrated to get x = R  + c. We may form our
augmented Lagrangian with either the integrated constraint or its
derivative.
+ c. We may form our
augmented Lagrangian with either the integrated constraint or its
derivative.
The kinetic energy has two parts, the energy of rotation of the hoop and the energy of the motion of its center of mass.94 The potential energy of the hoop decreases as the height decreases. Thus we may write the augmented Lagrangian:
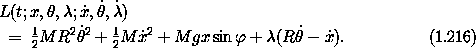
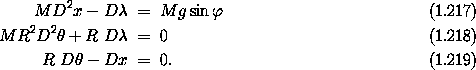
And by differentiation of the third Lagrange equation we obtain

By combining these equations we can solve for the dynamical quantities of interest. For this case of a rolling hoop the linear acceleration

is just half of what it would have been if the mass had just slid down
a frictionless plane without rotating. Note that for this hoop D2x
is independent of both M and R.
We see from the Lagrange equations
that D can be interpreted as the friction force involved
in enforcing the constraint. The frictional force of constraint is
can be interpreted as the friction force involved
in enforcing the constraint. The frictional force of constraint is

and the angular acceleration is

Systems with constraints that are not integrable are termed nonholonomic systems. A constraint is not integrable if it cannot be written in terms of an equivalent coordinate constraint. An example of a nonholonomic system is a ball rolling without slipping in a bowl. As the ball rolls it must turn so that its surface does not move relative to the bowl at the point of contact. This looks as if it might establish a relation between the location of the ball in the bowl and the orientation of the ball, but it doesn't. The ball may return to the same place in the bowl with different orientations depending on the intervening path it has taken. As a consequence, the constraints cannot be used to eliminate any coordinates.
What are the equations of motion governing nonholonomic systems?
For the restricted set of systems with nonholonomic
constraints that are linear in the velocities, it is widely
reported95
that the equations of motion are as follows. Let  have the form
have the form

a state function that is linear in the velocities. We assume  is not a total time derivative. If L is a Lagrangian for the
unconstrained system, then the equations of motion are
asserted to be
is not a total time derivative. If L is a Lagrangian for the
unconstrained system, then the equations of motion are
asserted to be
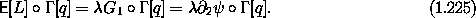
With the constraint  = 0, the system is closed and the
evolution of the system is determined. Note that these equations are
identical to the Lagrange equations
(1.212) for the case that
= 0, the system is closed and the
evolution of the system is determined. Note that these equations are
identical to the Lagrange equations
(1.212) for the case that  is a
total time derivative, but here the derivation of those equations is
no longer valid.
is a
total time derivative, but here the derivation of those equations is
no longer valid.
An essential step in the
derivation of the Lagrange equations for coordinate constraints  = 0 with
= 0 with  2
2  = 0 was to
note that two conditions must be satisfied:
= 0 was to
note that two conditions must be satisfied:


Because E [L] o  [q] is orthogonal to
[q] is orthogonal to  and
and  is constrained to be orthogonal to
is constrained to be orthogonal to
 1
1  o
o  [q] , the two must be parallel at
each moment:
[q] , the two must be parallel at
each moment:

The Lagrange equations for derivative constraints were derived from this.
This derivation does not go through if the constraint function
depends on velocity. In this case, for a
variation  to be consistent with the velocity-dependent
constraint function
to be consistent with the velocity-dependent
constraint function  it must satisfy
(see equation 1.179)
it must satisfy
(see equation 1.179)
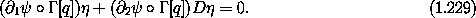
We may no longer eliminate  by the same argument, because
by the same argument, because  is no longer orthogonal to
is no longer orthogonal to  1
1  o
o  [q], and we
cannot rewrite the constraint as a coordinate constraint because
[q], and we
cannot rewrite the constraint as a coordinate constraint because
 is, by assumption, not integrable.
is, by assumption, not integrable.
The following is the derivation of the nonholonomic equations from
Arnold et al. [6], translated into our notation.
Define a ``virtual velocity''  to be any velocity satisfying
to be any velocity satisfying

The ``principle of d'Alembert-Lagrange,'' according to Arnold, states that

for any virtual velocity  .
Because
.
Because  is arbitrary except that it is required to be orthogonal
to
is arbitrary except that it is required to be orthogonal
to  2
2  o
o  [q] and any such
[q] and any such  is orthogonal
to E [L] o
is orthogonal
to E [L] o  [q], then
[q], then  2
2  o
o  [q]
must be parallel to E [L] o
[q]
must be parallel to E [L] o  [q].
So
[q].
So

which are the nonholonomic equations.
To convert the stationary action equations to the equations of Arnold
we must do the following. To get from
equation (1.226) to
equation (1.231), we must replace  by
by
 . However, to get from equation (1.229) to
equation (1.230), we must set
. However, to get from equation (1.229) to
equation (1.230), we must set  = 0 and
replace D
= 0 and
replace D by
by  . All ``derivations'' of the nonholonomic
equations have similar identifications. It comes down to this: the
nonholonomic equations do not follow from the action principle. They
are something else. Whether they are correct or not depends on
whether or not they agree with experiment.
. All ``derivations'' of the nonholonomic
equations have similar identifications. It comes down to this: the
nonholonomic equations do not follow from the action principle. They
are something else. Whether they are correct or not depends on
whether or not they agree with experiment.
For systems with either coordinate constraints or derivative constraints, we
have found that the Lagrange equations can be derived from a
Lagrangian that is augmented with the constraint. However, if the
constraints are not integrable the Lagrange equations for the
augmented Lagrangian are not the same as the nonholonomic
system (equations 1.225).96
Let L' be an augmented Lagrangian with non-integrable constraint  :
:
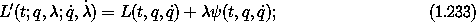
then the Lagrange equations associated with the coordinates are
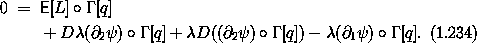
The Lagrange equation associated with  is just the constraint equation
is just the constraint equation

An interesting feature of these equations is that
they
involve both  and D
and D . Thus the usual state
variables q and Dq, with the constraint, are not sufficient
to determine a full set of initial conditions for the derived Lagrange
equations; we need to specify an initial value for
. Thus the usual state
variables q and Dq, with the constraint, are not sufficient
to determine a full set of initial conditions for the derived Lagrange
equations; we need to specify an initial value for  as well.
as well.
In general, for any particular physical system, equations (1.225) and (1.234) are not the same, and in fact they have different solutions. It is not apparent that either set of equations accurately models the physical system. The first approach to nonholonomic systems is not justified by extension of the arguments for the holonomic case and the other is not fully determined. Perhaps this indicates that the models are inadequate, that more details of how the constraints are maintained need to be specified.
88 Given any acceptable variation, we may make another acceptable variation by multiplying the given one by a bump function that emphasizes any particular time interval.
89 We take two tuple-valued functions of time to be orthogonal if at each instant the dot product of the tuples is zero. Similarly, tuple-valued functions are considered parallel if at each moment one of the tuples is a scalar multiple of the other. The scalar multiplier is in general a function of time.
90 Recall that the Euler-Lagrange operator E has the property
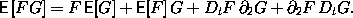
91 This constraint has the same form as those used in the demonstration that L = T - V can be used for rigid systems. Here it is a particular example of a more general set of constraints.
92 Indeed, if we had scaled
the constraint equations as we did in the discussion of Newtonian
constraint forces, we could have identified  with the the
magnitude of the constraint force F. However, though
with the the
magnitude of the constraint force F. However, though  will
in general be related to the constraint forces it will not be one of
them. We chose to leave the scaling as it naturally appeared rather
than make things turn out artificially pretty.
will
in general be related to the constraint forces it will not be one of
them. We chose to leave the scaling as it naturally appeared rather
than make things turn out artificially pretty.
93 This example appears in [20], pp. 49-51,
94 We will see in chapter 2 how to
compute the kinetic energy of rotation, but for now the answer is
(1/2) M R2  2.
2.
95 For some treatments of nonholonomic systems see, for example, Whittaker [46], Goldstein [20], Gantmakher [19], or Arnold et al. [6].
96 Arnold et al. [6] call the variational mechanics with the constraints added to the Lagrangian Vakonomic mechanics.