A function of the state of the system that is constant along a solution path is called a conserved quantity or a constant of motion. If C is a conserved quantity, then
for solution paths q. Following historical practice we also refer to constants of the motion as integrals of the motion.79 In this section, we will investigate systems with symmetry and find that symmetries are associated with conserved quantities. For instance, linear momentum is conserved in a system with translational symmetry, angular momentum is conserved if there is rotational symmetry, energy is conserved if the system does not depend on the origin of time. We first consider systems for which a coordinate system can be chosen that expresses the symmetry naturally, and later discuss systems for which no coordinate system can be chosen that simultaneously expresses all symmetries.
If a Lagrangian L(t, q, v) does not depend on some particular coordinate qi, then
and the corresponding ith component of the Lagrange equations is
This is the same as80
is a conserved quantity. The function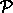 
is called
the momentum state function. The value of
the momentum state function is the generalized momentum. We
refer to the ith component of the generalized momentum as the
momentum conjugate to the ith coordinate.81
A generalized coordinate component that does not appear explicitly in
the Lagrangian is called a cyclic coordinate. The generalized
momentum component conjugate to any cyclic coordinate is a constant of
the motion. Its value is constant along realizable
paths; it may have different values on different paths. As we will
see, momentum is an important quantity even when it is not conserved.
Given the coordinate path q and the Lagrangian L, the momentum path p is
The momentum path is well defined for any path q. If the path is realizable and the Lagrangian does not depend on qi, then pi is a constant function
The constant value of pi may be different for different trajectories.
The free-particle Lagrangian L(t, x, v) = (1/2) mv2 is independent
of x. So the momentum state function, 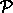(t, q, v) = mv, is
conserved along realizable paths. The momentum path p for the
coordinate path q is p(t) = 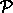o 
[q](t) = m Dq(t).
For a realizable path Dp(t) = 0. For the free particle the
usual linear momentum is conserved for realizable paths.
For a particle in a central force field (section 1.6), the Lagrangian
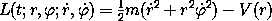
depends on r but is independent of
. The momentum state function is
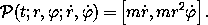
It has two components. The first component, the ``radial momentum,'' is not conserved. The second component, the ``angular momentum,'' is conserved along any solution trajectory.
If the central-potential problem had been expressed in rectangular coordinates, then all of the coordinates would have appeared in the Lagrangian. In that case there would not be any obvious conserved quantities. Nevertheless, the motion of the system does not depend on the choice of coordinates, so the angular momentum is still conserved.
We see that there is great advantage in making a judicious choice for the coordinate system. If we can choose the coordinates so that a symmetry of the system is reflected in the Lagrangian by the absence of some coordinate component, then the existence of a corresponding conserved quantity will be automatic.82
Momenta are conserved by the motion if the Lagrangian does not depend
on the corresponding coordinate. There is another constant of the
motion, the energy, if the Lagrangian L(t, q, 
) does not
depend explicitly on the time: 
0 L = 0.
Consider the time derivative of the Lagrangian along a solution path q:
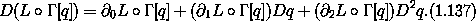
Using Lagrange's equations to rewrite the second term yields
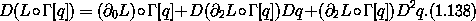
Isolating 0 L and combining the first two terms
on the right side gives
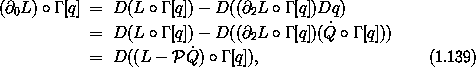
where, as before,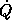 
selects the velocity from the state. So
we see that if 0 L = 0 then
is conserved along realizable paths.
The function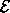 
is called the energy state function.83
Let E = 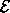o [q] denote the
energy function on the path q.
The energy function has a
constant value along any realizable trajectory if the Lagrangian has no explicit
time dependence; the energy E may have a different
value for different trajectories. A system that has no explicit time
dependence is called autonomous.
Given a Lagrangian procedure L, we may compute the energy:
(define (Lagrangian->energy L)
(let ((P ((partial 2) L)))
(- (* P velocity) L)))
In some cases the energy can be written as the sum of kinetic and
potential energies. Suppose the system is composed of
particles with rectangular coordinates x
, the
movement of which may be subject to constraints, and that these rectangular
coordinates are some functions of the generalized coordinates q and
possibly time t: x = f(t, q). We form
the Lagrangian as L = T - V and compute the kinetic energy in terms
of q by writing the rectangular velocities in terms of the
generalized velocities:
where v is the magnitude of v.
If the f functions do not depend explicitly on time
(0 f = 0), then the rectangular velocities are
homogeneous functions of the generalized velocities of degree 1, and
T is a homogeneous function of the generalized velocities of degree
2, because it is formed by summing the square of homogeneous functions
of degree 1. If T is a homogeneous function of degree 2 in the
generalized velocities then
where the second equality follows from Euler's theorem on homogeneous functions.84 The energy state function is
So if f is independent of time, the energy function can be rewritten
Notice that if V depends on time the energy is still the sum of the kinetic energy and potential energy, but the energy is not conserved.
The energy state function is always a well defined function, whether or not it can be written in the form T + V, and whether or not it is conserved along realizable paths.
Exercise 1.28.
An analogous result holds when the f depend explicitly on time.
a. Show that in this case the kinetic energy contains terms that are linear in the generalized velocities.
b. Show that, by adding a total time derivative, the Lagrangian can be written in the form L = A - B, where A is a homogeneous quadratic form in the generalized velocities and B is independent of velocity.
c. Show, using Euler's theorem, that the energy function is
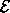= A + B.
An example in which terms that were linear in the velocity were removed from the Lagrangian by adding a total time derivative has already been given: the driven pendulum.
Exercise 1.29.
A particle of mass m slides off a horizontal cylinder of radius R
in a uniform gravitational field with acceleration g. If the
particle starts close to the top of the cylinder with zero initial speed, with what
angular velocity does it leave the cylinder?
One important physical system is the motion of a particle in a central
field in three dimensions, with an arbitrary potential energy V(r)
depending only on the radius. We will describe this system in
spherical coordinates r, 
, and , where is the
colatitude and is the longitude. The kinetic energy has three
terms:
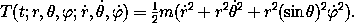
As a procedure:
(define ((T3-spherical m) state)
(let ((q (coordinate state))
(qdot (velocity state)))
(let ((r (ref q 0))
(theta (ref q 1))
(rdot (ref qdot 0))
(thetadot (ref qdot 1))
(phidot (ref qdot 2)))
(* 1/2 m
(+ (square rdot)
(square (* r thetadot))
(square (* r (sin theta) phidot)))))))
The Lagrangian is then formed by subtracting the potential energy:
(define (L3-central m Vr)
(define (Vs state)
(let ((r (ref (coordinate state) 0)))
(Vr r)))
(- (T3-spherical m) Vs))
Let's first look at the generalized forces (the derivatives of the Lagrangian with respect to the generalized coordinates). We compute these with a partial derivative with respect to the coordinate argument of the Lagrangian:
(show-expression
(((partial 1) (L3-central 'm (literal-function 'V)))
(up 't
(up 'r 'theta 'phi)
(up 'rdot 'thetadot 'phidot))))
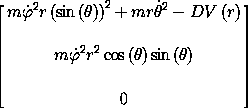
The component of the force is zero because
does not appear in the Lagrangian (it is a cyclic variable).
The corresponding momentum component is conserved. Compute
the momenta:
(show-expression
(((partial 2) (L3-central 'm (literal-function 'V)))
(up 't
(up 'r 'theta 'phi)
(up 'rdot 'thetadot 'phidot))))
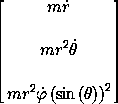
The momentum conjugate to is conserved. This is the z component of
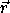the angular momentum 
× (m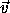 
), for vector
position 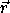and linear momentum m 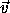. We can show this by
writing the z component of the angular momentum in
spherical coordinates:
(define ((ang-mom-z m) state)
(let ((q (coordinate state))
(v (velocity state)))
(ref (cross-product q (* m v)) 2)))
(define (s->r state)
(let ((q (coordinate state)))
(let ((r (ref q 0))
(theta (ref q 1))
(phi (ref q 2)))
(let ((x (* r (sin theta) (cos phi)))
(y (* r (sin theta) (sin phi)))
(z (* r (cos theta))))
(up x y z)))))
(show-expression
((compose (ang-mom-z 'm) (F->C s->r))
(up 't
(up 'r 'theta 'phi)
(up 'rdot 'thetadot 'phidot))))
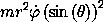
The choice of the z-axis is arbitrary, so the conservation of any
component of the angular momentum implies the conservation of all
components. Thus the total angular momentum is conserved. We can
choose the z-axis so all of the angular momentum is in the z
component. The angular momentum must be perpendicular to both the
radius vector and the linear momentum vector. Thus the motion is
planar, = 
/2, and 
= 0. Planar motion in a
central-force field was discussed in section 1.6.
We can also see that the energy state function computed from the Lagrangian for a central field is in fact T + V:
(show-expression
((Lagrangian->energy (L3-central 'm (literal-function 'V)))
(up 't
(up 'r 'theta 'phi)
(up 'rdot 'thetadot 'phidot))))
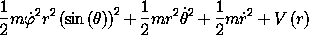
The energy is conserved because the Lagrangian has no explicit time dependence.
Exercise 1.30. Driven spherical pendulum
A spherical pendulum is a massive bob, subject to uniform gravity,
that may swing in three dimensions, but remains at a given distance
from the pivot. Formulate a Lagrangian for a spherical pendulum,
driven by vertical motion of the pivot. What symmetry(ies) can you find?
Find coordinates that express the symmetry. What is conserved? Give
analytic expression(s) for the conserved quantity(ies).
We have seen that if a system has a symmetry and if a coordinate system can be chosen so that the Lagrangian does not depend on the coordinate associated with the symmetry, then there is a conserved quantity associated with the symmetry. However, there are more general symmetries that no coordinate system can fully express. For example, motion in a central potential is spherically symmetric (the dynamical system is invariant under rotations about any axis), but the expression of the Lagrangian for the system in spherical coordinates exhibits symmetry around only one axis. More generally, a Lagrangian has a symmetry if there is a coordinate transformation that leaves the Lagrangian unchanged. A continuous symmetry is a parametric family of symmetries. Noether proved that for any continuous symmetry there is a conserved quantity.
Consider a parametric coordinate transformation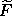 
with
parameter s:
To this parametric coordinate transformation there corresponds a
parametric state transformation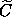 
:
We require that the transformation 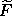(0) be
the identity coordinate transformation x' = 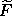(0)(t, x'),
and as a consequence 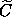(0) is the identity state
transformation ( t, x', v' ) = 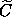(0)(t, x', v').
The Lagrangian L has a continuous symmetry corresponding to
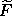if it is invariant under the transformations
for any s. The Lagrangian L is the same function as the transformed
Lagrangian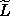 
(s).
That 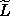(s) = L for any s implies D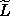(s) =
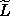0. Explicitly, (s) is
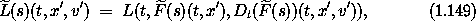
where we have rewritten the velocity component of 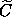(s)
in terms of the total time derivative.
The derivative of 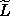is zero:
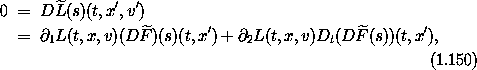
where we have used the fact that85
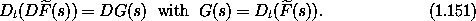
On a realizable path q we can use the Lagrange equations to rewrite the first term:
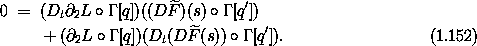
For s = 0 the paths q and q' are the same, because
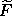(0) is the identity, so [q] =
[q'] and this equation becomes
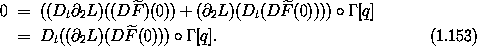
is conserved along solution trajectories. This is Noether's integral. The integral is the product of the momentum and a vector associated with the symmetry.
For example, consider the central potential Lagrangian in rectangular coordinates:
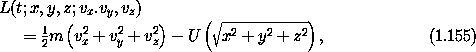
and a parametric rotation Rz(s) about the z axis
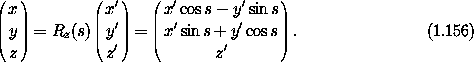
The rotation is an orthogonal transformation so
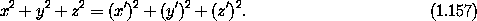
Differentiating along a path, we get
so the velocities also transform by an orthogonal transformation, and vx2 + vy2 + vz2 = (vx')2 + (vy')2 + (vz')2 . Thus
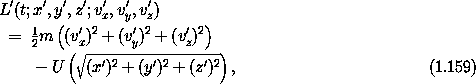
and we see that L' is precisely the same function as L.
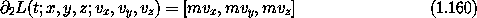
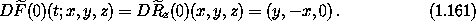
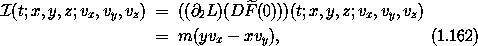
which we recognize as minus the z component of the angular momentum:
× (m ).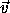
Since the Lagrangian is preserved by any continuous rotational
symmetry, all components of the vector angular momenta are conserved
for the central-potential problem.
The procedure calls ((Rx angle-x) q), ((Ry angle-y) q), and ((Rz angle-z) q) rotate the rectangular tuple q about the indicated axis by the indicated angle.86 We use these to make a parametric coordinate transformation F-tilde:
(define (F-tilde angle-x angle-y angle-z)
(compose (Rx angle-x) (Ry angle-y) (Rz angle-z) coordinate))
A Lagrangian for motion in a central potential is
(define ((L-central-rectangular m U) state)
(let ((q (coordinate state))
(v (velocity state)))
(- (* 1/2 m (square v)) (U (sqrt (square q))))))
The Noether integral is then
(define Noether-integral
(let ((L (L-central-rectangular
'm (literal-function 'U))))
(* ((partial 2) L) ((D F-tilde) 0 0 0))))
(print-expression
(Noether-integral
(up 't
(up 'x 'y 'z)
(up 'vx 'vy 'vz))))
(down (+ (* m vy z) (* -1 m vz y))
(+ (* m vz x) (* -1 m vx z))
(+ (* m vx y) (* -1 m vy x)))
We get all three components of the angular momentum.
79 In older literature conserved quantities are sometimes called first integrals.
80 The derivative of a component is equal to the component of the derivative.
81 Observe that we indicate a component of the generalized momentum with a subscript, and a component of the generalized coordinates with a superscript. These conventions are consistent with those commonly used in tensor algebra, which is sometimes helpful in working out complex problems.
82 In general, conserved quantities in a physical system are associated with continuous symmetries, whether or not one can find a coordinate system in which the symmetry is apparent. This powerful notion was formalized and a theorem linking conservation laws with symmetries was proved by Noether early in the 20th century. See section 1.8.4 on Noether's theorem.
83 The sign of the energy state function is a matter of convention.
84 A function f is homogenous of degree n if and only if f(ax) = anf(x). Euler's theorem says that if f is a homogeneous function of degree n, then Df(x)x = nf(x). The proof is as follows: Let gx(a) = f(ax). Then Dgx(a) = Df(ax)x. But gx(a) = anf(x) by the definition of homogeneity. Therefore Dgx(a) = nan-1f(x). Equating these, we find Df(ax)x = nan-1f(x). Specializing to a = 1 we obtain Df(x)x = nf(x) as required.
85 The total time derivative is like a derivative with respect to a
real-number argument in that it does not generate structure, so it can
commute with derivatives that generate structure. Be careful, though:
it may not commute with some derivatives for other reasons. For
example, Dt 1 (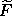(s)) is the same as 1
Dt (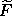(s)), but Dt 2 (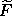(s))
is not the same as 2 Dt (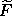(s)). The reason is
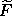that (s) does not depend on the velocity, but Dt
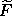((s)) does.
86 The definition of the procedure Rx is
(define ((Rx angle) q)
(let ((ca (cos angle)) (sa (sin angle)))
(let ((x (ref q 0)) (y (ref q 1)) (z (ref q 2)))
(up x
(- (* ca y) (* sa z))
(+ (* sa y) (* ca z))))))
The definitions of Ry and Rz are similar.
,