
We have all played with a top at one time or another. For the purposes of analysis we will consider an idealized top that does not wander around. Thus, an ideal top is a rotating rigid body, one point of which is fixed in space. Furthermore, the center of mass of the top is not at the fixed point, which is the center of rotation, and there is a uniform gravitational acceleration.
For our top we can take the Lagrangian to be the difference of the kinetic energy and the potential energy. We already know how to write the kinetic energy -- what is new here is that we must express the potential energy in terms of the configuration. In the case of a body in a uniform gravitational field this is easy. The potential energy is the sum of ``mgh'' for all the constituent particles:

where g is the gravitational acceleration, h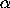 =
= 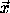
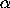 ·
· 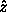 , and the unit
vector
, and the unit
vector 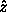 indicates which way is up. Rewriting the vector to
the constituents in terms of the vector
indicates which way is up. Rewriting the vector to
the constituents in terms of the vector 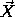 to the center of
mass, the potential energy is
to the center of
mass, the potential energy is
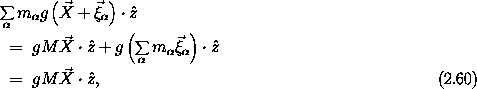
where the last sum is zero because the center of mass is the origin of
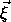
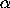 . So the potential energy of a body in a
gravitational field with uniform acceleration is very simple: it is
just Mgh, where M is the total mass and h =
. So the potential energy of a body in a
gravitational field with uniform acceleration is very simple: it is
just Mgh, where M is the total mass and h = 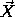 ·
· 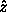 is the
height of the center of mass.
is the
height of the center of mass.
Here we consider an axisymmetric top (see figure 2.4). Such a top has an axis of symmetry of the mass distribution, so the center of mass is on the symmetry axis and the fixed point is also on the axis of symmetry.
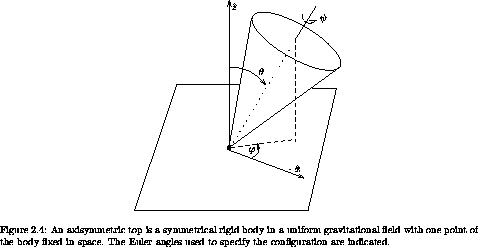
In order to write the Lagrangian we need to choose a set of generalized coordinates. If we choose them well we can take advantage of the symmetries of the problem. If the Lagrangian does not depend on a particular coordinate, the conjugate momentum is conserved, and the complexity of the system is reduced.
The axisymmetric top has two apparent symmetries. The fact that the mass distribution is axisymmetric implies that neither the kinetic nor potential energy is sensitive to the orientation of the top about that symmetry axis. Additionally, the kinetic and potential energy are insensitive to a rotation of the physical system about the vertical axis, because the gravitational field is uniform.
We can take advantage of these symmetries by choosing appropriate
coordinates, and we already have a coordinate system that
does the job -- the Euler angles.12 We
choose the reference orientation so that the symmetry axis is
vertical. The first Euler angle, 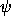 , expresses a rotation about the
symmetry axis. The next Euler angle,
, expresses a rotation about the
symmetry axis. The next Euler angle,  , is the tilt of the
symmetry axis of the top from the vertical. The third Euler angle,
, is the tilt of the
symmetry axis of the top from the vertical. The third Euler angle,
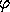 , expresses a rotation of the top about the z axis. The
symmetries of the problem imply that the first and third Euler angles
do not appear in the Lagrangian. As a consequence the momenta
conjugate to these angles are conserved quantities. Let's work out
the details.
, expresses a rotation of the top about the z axis. The
symmetries of the problem imply that the first and third Euler angles
do not appear in the Lagrangian. As a consequence the momenta
conjugate to these angles are conserved quantities. Let's work out
the details.
First, we develop the Lagrangian explicitly. The general form of the kinetic energy about a point is given by equation 2.30. The top is constrained so that it pivots about a fixed point that is not at the center of mass. So the moments of inertia that enter the kinetic energy are the moments of inertia of the top with respect to the pivot point, not with respect to the center of mass. If we know the moments of inertia about the center of mass we can write the moments of inertia about the pivot in terms of them (see exercise 2.2). So let's assume the principal moments of inertia of the top about the pivot are A, B, and C, and A = B because of the symmetry.13 We can use the computer to help us figure out the Lagrangian for this special case:
(show-expression
((T-rigid-body 'A 'A 'C)
(up 't
(up 'theta 'phi 'psi)
(up 'thetadot 'phidot 'psidot))))
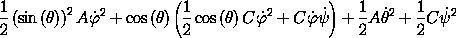
We can rearrange this a bit to get
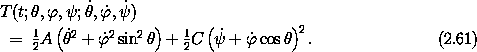
In terms of Euler angles, the potential energy is
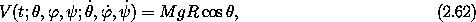
where R is the
distance of the center of mass from the pivot. The Lagrangian is L =
T - V. We see that the Lagrangian is indeed independent of
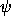 and
and 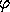 , as expected.
, as expected.
There is no particular reason to look at the Lagrange equations. We can assign that job to the computer when needed. However, we have already seen that it may be useful to examine the conserved quantities associated with the symmetries.
The energy is conserved, because the Lagrangian has no explicit time dependence. Also, the energy is the sum of the kinetic and potential energy E = T + V, because the kinetic energy is a homogeneous quadratic form in the generalized velocities. The energy is
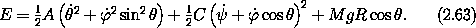
Two of the generalized coordinates do not appear in the Lagrangian, so
there are two conserved momenta. The momentum conjugate to 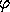 is
is
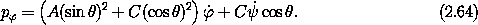

The state of the system at a moment is specified by the tuple ( t;
 ,
, 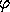 ,
, 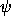 ;
; 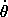 ,
, 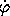 ,
, 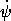 ). The
two coordinates
). The
two coordinates 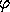 and
and 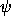 that do not appear in the
Lagrangian do not appear in the Lagrange equations or the conserved
momenta. So the evolution of the remaining four state variables,
that do not appear in the
Lagrangian do not appear in the Lagrange equations or the conserved
momenta. So the evolution of the remaining four state variables,
 ,
, 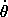 ,
, 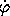 , and
, and 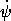 , depends
only on those remaining state variables. This subsystem for the top
has a four-dimensional state space. The variables that did not appear
in the Lagrangian can be determined by integrating the derivatives of
these variables, which are determined separately by solving the
independent subsystem.
, depends
only on those remaining state variables. This subsystem for the top
has a four-dimensional state space. The variables that did not appear
in the Lagrangian can be determined by integrating the derivatives of
these variables, which are determined separately by solving the
independent subsystem.
The evolution of the top is described by a four-dimensional subsystem
and two auxiliary quadratures.14
This subdivision is a consequence of choosing generalized coordinates
that incorporate the symmetries. However, the choice of generalized
coordinates that incorporate the symmetries also gives conserved
momenta. We can make use of these momenta to simplify the
formulation of the problem further. Each integral can be used to locally
eliminate one dimension of the subsystem. In this case the subsystem
has four dimensions and there are three integrals, so the system can
be completely reduced to quadratures. For the top, this can be done
analytically, but we think it is a waste of time to do so. Rather, we
are interested in extracting interesting features of the motion. We
concentrate on the energy integral and use the two conserved momenta
to eliminate 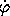 and
and 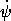 . After a bit of algebra we
find:
. After a bit of algebra we
find:
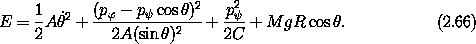
Along a path  , where D
, where D (t) is substituted for
(t) is substituted for
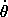 , this is an ordinary differential equation for
, this is an ordinary differential equation for
 . This differential equation involves various constants, some
of which are set by the initial conditions of the other state
variables. The solution of the differential equation for
. This differential equation involves various constants, some
of which are set by the initial conditions of the other state
variables. The solution of the differential equation for  involves no more than ordinary integrals.
So the top is essentially solved. We could continue this
argument to obtain the qualitative behavior of
involves no more than ordinary integrals.
So the top is essentially solved. We could continue this
argument to obtain the qualitative behavior of  : Using the
energy (2.66), we can plot the trajectories in the
plane of
: Using the
energy (2.66), we can plot the trajectories in the
plane of 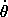 versus
versus  and see that the motion of
and see that the motion of
 is simply periodic. However, we will defer
continuing along this path until chapter 3, when we have developed more tools for analysis.
is simply periodic. However, we will defer
continuing along this path until chapter 3, when we have developed more tools for analysis.
Let's get real. Let's make a top out of an aluminum disk
with a steel rod through the center to make the pivot. Measuring the
top very carefully, we find that the moment of inertia of the top about
the symmetry axis is about 6.60 × 10-5 kg m2,
and the moment of inertia about the pivot point is about
3.28 × 10-4 kg m2. The combination gMR is about
0.0456 kg m2 s-2. We spin the top up with
an initial angular velocity of 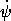 = 140 rad s-1
(about 1337 rpm). The top initially has
= 140 rad s-1
(about 1337 rpm). The top initially has 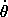 =
= 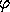 =
= 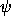 =
0 and is initially tilted with
=
0 and is initially tilted with  = 0.1 rad. We then
kick it so that
= 0.1 rad. We then
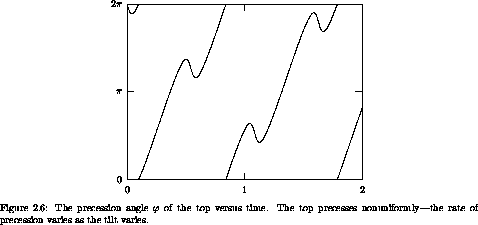
kick it so that 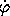 = - 15 rad s-1. Figures
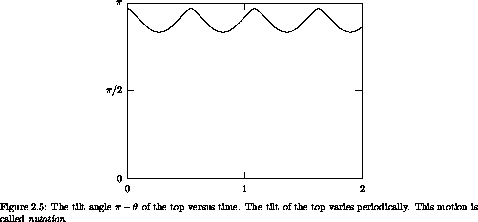
2.5-2.8 display aspects of
the evolution of the top for 2 seconds. The tilt of the top (measured
by
= - 15 rad s-1. Figures
2.5-2.8 display aspects of
the evolution of the top for 2 seconds. The tilt of the top (measured
by  ) varies in a periodic manner. The orientation about the
vertical is measured by
) varies in a periodic manner. The orientation about the
vertical is measured by 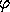 : we see that the top also precesses,
and the rate of precession varies with
: we see that the top also precesses,
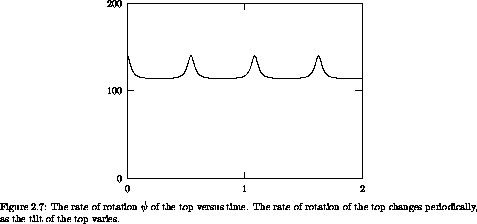
and the rate of precession varies with  . We also see that as
the top bobs up and down the rate of rotation of the top
oscillates -- the top spins faster when it is more vertical.
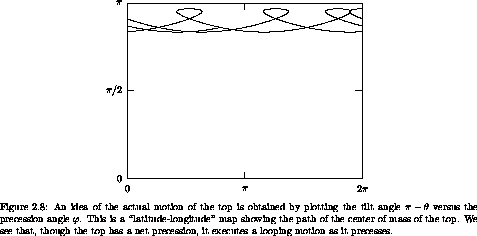
The plot of tilt versus precession angle shows that in this case
the top executes a looping motion. If we do not kick it but just let
it drop, then the loop disappears, leaving just a cusp. If we kick it
in the other direction, then there is no cusp nor any looping motion.
. We also see that as
the top bobs up and down the rate of rotation of the top
oscillates -- the top spins faster when it is more vertical.
The plot of tilt versus precession angle shows that in this case
the top executes a looping motion. If we do not kick it but just let
it drop, then the loop disappears, leaving just a cusp. If we kick it
in the other direction, then there is no cusp nor any looping motion.
Exercise 2.11. Kinetic energy of the top
The rotational kinetic energy of the top can be written in terms of
the principal moments of inertia with respect to the pivot point and
the angular velocity vector of rotation with respect to the pivot
point. Show that this formulation of the kinetic energy yields the
same value that one would obtain by computing the sum of the
rotational kinetic energy about its center of mass and the kinetic
energy of the motion of the center of mass.
Exercise 2.12. Nutation of the top
a. Carry out the algebra to obtain the
energy (2.66) in terms of  and
and 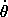 .
.
b. Numerically integrate the Lagrange equations for the top to
obtain figure 2.5,  versus time.
versus time.
c. Note that the energy is a differential equation for
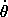 in terms of
in terms of  , with conserved quantities
p
, with conserved quantities
p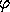 , p
, p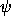 , and E determined by initial conditions. Can we
use this differential equation to obtain
, and E determined by initial conditions. Can we
use this differential equation to obtain  as a function of
time? Explain.
as a function of
time? Explain.
Exercise 2.13. Precession of the top
Consider a top that is rotating so that  is constant.
is constant.
a. Using the angular momentum integrals, compute the rate of
precession 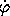 as a function of the conserved angular
momenta and the equilibrium value of
as a function of the conserved angular
momenta and the equilibrium value of  .
.
b. For  to be at an equilibrium the acceleration D2
to be at an equilibrium the acceleration D2
 must be zero. Use the Lagrange equation for
must be zero. Use the Lagrange equation for  to find
the rate of precession
to find
the rate of precession 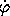 at the equilibrium in terms of the
equilibrium
at the equilibrium in terms of the
equilibrium  and
and 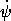 .
.
c. Find an approximate expression for the precession rate in
the limit that 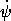 is large.
is large.
d. The Newtonian rule is that the rate of change of the angular momentum is the torque. Assume the top is spinning so fast that the angular momentum is nearly the same as the angular momentum of rotation about the symmetry axis. By equating the rate of change of this vector angular momentum to the gravitational torque on the center of mass develop an approximate formula for the precession rate.
e. Numerically integrate the top to check your deductions.
12 That the axisymmetric top can be solved in Euler angles is, no doubt, the reason for the traditional choice of the definition of these. For other problems, the Euler angles may offer no particular advantage.
13 Here, we do not require that C be larger than A = B, because they are not measured with respect to the center of mass.
14 Traditionally, evaluating a definite integral is known as performing a quadrature.