
The rotation of planets and natural satellites is affected by the gravitational forces from other celestial bodies. As an extended application of the Lagrangian method for forced rigid bodies, we consider the rotation of celestial objects subject to gravitational forces.
We first develop the form of the potential energy for the gravitational interaction of an extended body with an external point mass. With this potential energy and the usual rigid-body kinetic energy we can form Lagrangians that model a number of systems. We will take an initial look at the rotation of the Moon and Mercury; later, after we have developed more tools, we will return to study these systems.
The first task is to develop convenient expressions for the gravitational potential energy of the interaction of a rigid body with a distant mass point. A rigid body can be thought of as made of a large number of mass elements, subject to rigid coordinate constraints. We have seen that the kinetic energy of a rigid body is conveniently expressed in terms of the moments of inertia of the body and the angular velocity vector, which in turn can be represented in terms of a suitable set of generalized coordinates. The potential energy can be developed in a similar manner. We first represent the potential energy in terms of moments of the mass distribution and later introduce generalized coordinates as particular parameters of the potential energy.
The gravitational potential energy of a mass point and a rigid body (see figure 2.9) is the sum of the potential energy of the mass point with each mass element of the body:

where M' is the mass of the external point mass, r is the
distance between the point mass and the constituent mass element with
index
is the
distance between the point mass and the constituent mass element with
index  , m
, m is the mass of this constituent element,
and G is the gravitational constant. Let R be the distance of the
center of mass of the rigid body from the point mass; R is the
magnitude of the vector
is the mass of this constituent element,
and G is the gravitational constant. Let R be the distance of the
center of mass of the rigid body from the point mass; R is the
magnitude of the vector  -
- 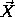 , where the external mass
point has position
, where the external mass
point has position  and the center of mass of the rigid body has position
and the center of mass of the rigid body has position
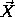 . The vector from the center of mass to the constituent with
index
. The vector from the center of mass to the constituent with
index  is
is 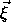
 and has magnitude
and has magnitude

 . The distance r
. The distance r is then given by the law of
cosines as r
is then given by the law of
cosines as r 2 = R2 +
2 = R2 + 
 2 - 2
2 - 2 
 R cos
R cos

 , where
, where 
 is the angle between
is the angle between  -
-
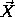 and
and 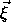
 . The potential energy is then
. The potential energy is then
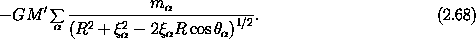
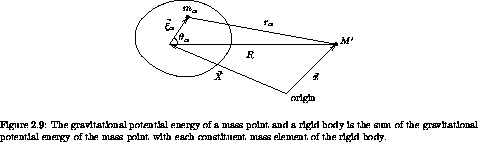
This is complete, but we need to find a representation that does not mention each constituent.
Typically, the size of celestial bodies is small compared to the
distance between them. We can make use of this to find a more
compact representation of the potential energy. If we expand the
potential energy in the small ratio 
 /R we find
/R we find

where Pl is the lth Legendre polynomial.15 Interchanging the order of the summations yields:

Successive terms in this expansion of the potential energy typically
decrease very rapidly because celestial bodies are small
compared to the distance between them. We can compute an upper bound to the
size of these terms by replacing each factor in the sum over
 by an upper bound. The Legendre polynomials all have
magnitudes less than one for arguments in the range - 1 to 1. The
distances
by an upper bound. The Legendre polynomials all have
magnitudes less than one for arguments in the range - 1 to 1. The
distances 
 are all less than some maximum extent of the
body
are all less than some maximum extent of the
body  max. The sum over m
max. The sum over m times these upper bounds is
just the total mass M times the upper bounds. Thus
times these upper bounds is
just the total mass M times the upper bounds. Thus
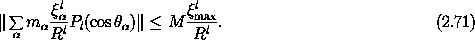
We see that the upper bound on successive terms decreases by a factor
 max / R. Successive terms may be smaller still. For
large bodies the gravitational force is strong enough to overcome the
internal material strength of the body, so the body, over time,
becomes nearly spherical. Successive terms in the expansion of the
potential are measures of the deviation of the mass distribution from
a spherical mass distribution. Thus for large bodies the higher-order
terms are small because the bodies are nearly spherical.
max / R. Successive terms may be smaller still. For
large bodies the gravitational force is strong enough to overcome the
internal material strength of the body, so the body, over time,
becomes nearly spherical. Successive terms in the expansion of the
potential are measures of the deviation of the mass distribution from
a spherical mass distribution. Thus for large bodies the higher-order
terms are small because the bodies are nearly spherical.
Consider the first few terms in l. For l = 0 the sum over  just gives the total mass M of the rigid body. For l = 1 the sum
over
just gives the total mass M of the rigid body. For l = 1 the sum
over  is zero, as a consequence of choosing the origin of the
is zero, as a consequence of choosing the origin of the
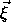
 to be the center of mass. For l = 2 we have to do
a little more work. The sum involves second moments of the mass
distribution, and can be written in terms of moments of inertia of
the rigid body:
to be the center of mass. For l = 2 we have to do
a little more work. The sum involves second moments of the mass
distribution, and can be written in terms of moments of inertia of
the rigid body:
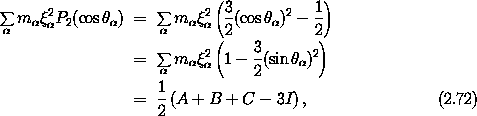
where A, B, and C are the principal moments of inertia, and I is the moment of inertia of the rigid body about the line between the center of mass of the body to the external point mass. The moment I depends on the orientation of the rigid body relative to the line between the bodies. The contributions to the potential energy up to l = 2 are then16
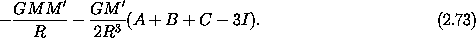
Let  = cos
= cos  a, ß = cos
a, ß = cos  b, and
b, and  =
cos
=
cos  c be the direction cosines of the angles
c be the direction cosines of the angles
 a,
a,  b and
b and  c between the
principal axes hata,
c between the
principal axes hata, 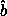 , and
, and 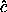 and the line between
the center of mass and the point mass.17
A little algebra shows that I =
and the line between
the center of mass and the point mass.17
A little algebra shows that I =
 2 A + ß2 B +
2 A + ß2 B +  2 C. The potential energy is then
2 C. The potential energy is then
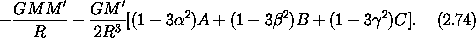
This is a good first approximation to the potential energy of interaction for most situations in the solar system; if we intended to land on the Moon we probably would want to take into account higher-order terms in the expansion.
a. Fill in the details that show that the sum over constituents
in equation (2.72) can be expressed as written in
terms of moments of inertia. In particular, show that
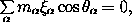
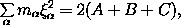
and that
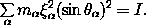
b. Show that if the principal moments of inertia of a rigid body are A,
B, and C, then the moment of inertia about an axis that goes
through the center of mass of the body with direction cosines
 , ß, and
, ß, and  relative to the principal axes is
relative to the principal axes is
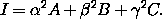
The approximation to the potential energy that we have derived can be used for a number of different problems. It can be used to investigate the effect of oblateness on the evolution of an artificial satellite about the Earth, or to incorporate the effect of planetary oblateness on the evolution of the orbits of natural satellites, such as the Moon or the Galilean satellites of Jupiter. However, as the principal application here, we will use it to investigate the rotational dynamics of natural satellites and planets.
The potential energy depends on the position of the point
mass relative to the rigid body and on the orientation of the rigid
body. Thus the changing orientation is coupled to the orbital
evolution; each affects the other. However, in many situations the
effect of the orientation of the body on the evolution of the orbit
may be ignored. One way to see this is to look at the
relative magnitudes of the two terms in the potential
energy (2.74). We already know that the second
term is guaranteed to be smaller than the first by a factor of
( max / R)2, but often it is much smaller still because
the body involved is nearly spherical. For example, the radius of the
Moon is about a third the radius of the Earth and the distance to the
Moon is about 60 Earth-radii. So the second term is smaller than the
first by a factor of order 10-4 due to the size factors. In
addition, the Moon is roughly spherical and for any orientation the
combination A + B + C - 3I is of order 10-4C. Now C is
itself of order (2/5)MR2, because the density of
the Moon does not vary strongly with radius. So for the Moon
the second term is of order 10-8 relative to the first. Even
radical changes in the orientation of the Moon would have little
dynamical effect on its orbit.
max / R)2, but often it is much smaller still because
the body involved is nearly spherical. For example, the radius of the
Moon is about a third the radius of the Earth and the distance to the
Moon is about 60 Earth-radii. So the second term is smaller than the
first by a factor of order 10-4 due to the size factors. In
addition, the Moon is roughly spherical and for any orientation the
combination A + B + C - 3I is of order 10-4C. Now C is
itself of order (2/5)MR2, because the density of
the Moon does not vary strongly with radius. So for the Moon
the second term is of order 10-8 relative to the first. Even
radical changes in the orientation of the Moon would have little
dynamical effect on its orbit.
We can learn some important qualitative aspects of the orientation dynamics by studying a simplified model problem. First, we assume that the body is rotating about its largest moment of inertia. This is a natural assumption. Remember that for a free rigid body the loss of energy while conserving angular momentum leads to rotation about the largest moment of inertia. This is observed for most bodies in the solar system. Next, we assume that the spin axis is perpendicular to the orbital motion. This is a good approximation for the rotation of natural satellites, and is a natural consequence of tidal friction -- dissipative solid-body tides raised on the satellite by the gravitational interaction with the planet. Finally, for simplicity we take the rigid body to be moving on a fixed elliptic orbit. This may approximate the motion of some physical systems, provided the time scale of the evolution of the orbit is large compared to any time scale associated with the rotational dynamics we are investigating. So we have a nice toy problem, one that has been used to investigate the rotational dynamics of Mercury, the Moon, and other natural satellites. It makes specific predictions concerning the rotation of Phobos, a satellite of Mars, that can be compared with observations. It provides a basic explanation of the fact that Mercury rotates precisely three times for every two orbits it completes, and is the starting point for understanding the chaotic tumbling of Saturn's satellite Hyperion.
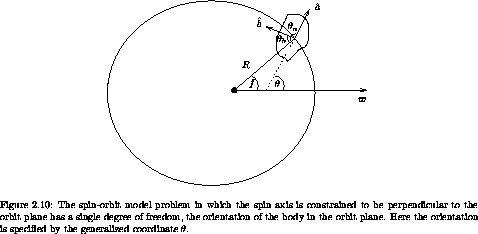
We are assuming that the orbit does not change or precess. The orbit
is an ellipse with the point mass at a focus of the ellipse. The
angle f (see figure 2.10) measures the position of
the rigid body in its orbit relative to the point in the orbit at
which the two bodies are closest.18
We assume the orbit is a fixed ellipse, so the angle f and the
distance R are periodic functions of time, with period equal to the
orbit period. With the spin axis constrained to be perpendicular to
the orbit plane, the orientation of the rigid body is specified by a
single degree of freedom: the orientation of the body about the spin
axis. We specify this orientation by the generalized coordinate
 that measures the angle to the hata principal axis from
the same line from which we measure f, the line through the point of closest
approach.
that measures the angle to the hata principal axis from
the same line from which we measure f, the line through the point of closest
approach.
Having specified the coordinate system, we can work out the details of the kinetic and potential energies, and thus find the Lagrangian. The kinetic energy is

where C is the moment of inertia about the spin axis and the
angular velocity of the body about the  axis is
axis is
 . There is no component of angular velocity on the
other principal axes.
. There is no component of angular velocity on the
other principal axes.
To get an explicit expression for the potential energy we must write
the direction cosines in terms of  and f:
and f:  = cos
= cos
 a = - cos (
a = - cos ( - f), ß = cos
- f), ß = cos  b = sin (
b = sin ( - f), and
- f), and  = cos
= cos  c = 0 because the
c = 0 because the 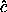 axis is
perpendicular to the orbit plane. The potential energy is then
axis is
perpendicular to the orbit plane. The potential energy is then
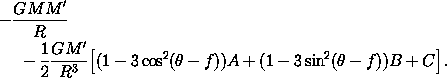
Since we are assuming that the orbit is given, we need
keep only terms that depend on  . Expanding the squares of
the cosine and the sine in terms of the double angles and dropping
all the terms that do not depend on
. Expanding the squares of
the cosine and the sine in terms of the double angles and dropping
all the terms that do not depend on  , we find the
potential energy for the orientation19
, we find the
potential energy for the orientation19
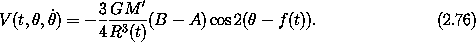
A Lagrangian for the model spin-orbit coupling problem is then L = T - V:
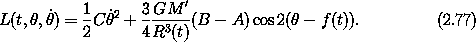
We introduce the dimensionless ``out-of-roundness'' parameter

and use the fact that the orbit frequency n satisfies Kepler's third law
n2 a3 = G(M + M'), which is approximately n2 a3 = GM' for a
small body in orbit around a much more massive one (M << M').
In terms of  and n the spin-orbit Lagrangian
is
and n the spin-orbit Lagrangian
is
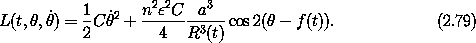
This is a problem with one degree of freedom with terms that vary periodically with time.
The Lagrange equations are derived in the usual manner:
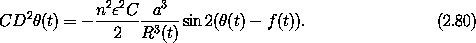
The equation of motion is very similar to that of the periodically driven pendulum. The main difference here is that not only is the strength of the acceleration changing periodically, but in the spin-orbit problem the center of attraction is also varying periodically.
We can give a physical interpretation of this equation of motion. It
states that the rate of change of the angular momentum is equal to the
applied torque. The torque on the body arises because the body is out
of round and the gravitational force varies as the inverse square of
the distance. Thus the force per unit mass on the near side of the
body is a little more than the acceleration of the body as a whole, and the
force per unit mass on the far side of the body is a little less than
the acceleration of the body as a whole. Thus, relative to the
acceleration of the body as a whole, the far side is forced outward
while the inner part of the body is forced inward. The net effect is
a torque on the body that tries to align the long axis of the body
with the line to the external point mass. If  is a bit larger
than f then there is a negative torque, and if
is a bit larger
than f then there is a negative torque, and if  is a bit
smaller than f then there is a positive torque, both of which would
align the long axis with the planet if given a fair chance. The
torque arises because of the difference of the inverse R2 force
across the body, so the torque is proportional to R-3. There is
a torque only if the body is out of round, for otherwise there is no
handle to pull on. This is reflected in the factor B - A
in the expression for the torque. The potential depends only
on the moment of inertia, and thus the body has the same dynamics if it is
rotated by 180o. The factor of 2 in the argument of sine
reflects this symmetry. This torque is called the ``gravity gradient
torque.''
is a bit
smaller than f then there is a positive torque, both of which would
align the long axis with the planet if given a fair chance. The
torque arises because of the difference of the inverse R2 force
across the body, so the torque is proportional to R-3. There is
a torque only if the body is out of round, for otherwise there is no
handle to pull on. This is reflected in the factor B - A
in the expression for the torque. The potential depends only
on the moment of inertia, and thus the body has the same dynamics if it is
rotated by 180o. The factor of 2 in the argument of sine
reflects this symmetry. This torque is called the ``gravity gradient
torque.''
To compute the evolution requires a lot of detailed preparation
similar to what has been done for other problems. There are many
interesting phenomena to explore. We can take parameters appropriate
for the Moon and find that Mr. Moon does not constantly point the
same face to the Earth, but instead constantly shakes his head in
dismay at what goes on here. If we nudge the Moon a bit, say by
hitting it with an asteroid, we find that the long axis oscillates
back and forth with respect to the direction that points to the Earth.
For the Moon, the orbital eccentricity is currently about 0.05, and
the out-of-roundness parameter is about  = 0.026.
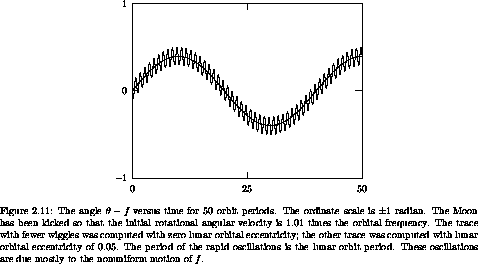
Figure 2.11 shows the angle
= 0.026.
Figure 2.11 shows the angle  - f as
a function of time for two different values of the ``lunar''
eccentricity. The plot spans 50 lunar orbits, or a little under four
years. This Moon has been kicked by a large asteroid and has initial
rotational angular velocity
- f as
a function of time for two different values of the ``lunar''
eccentricity. The plot spans 50 lunar orbits, or a little under four
years. This Moon has been kicked by a large asteroid and has initial
rotational angular velocity  equal to 1.01 times the
orbit frequency. The initial orientation is
equal to 1.01 times the
orbit frequency. The initial orientation is  = 0. The smooth
trace shows the evolution if the orbital eccentricity is set to zero.
We see an oscillation with a period of about 40 lunar orbits or
about three years. The more wiggly trace shows the evolution of
= 0. The smooth
trace shows the evolution if the orbital eccentricity is set to zero.
We see an oscillation with a period of about 40 lunar orbits or
about three years. The more wiggly trace shows the evolution of  -
f with an orbital eccentricity of 0.05, near the current lunar
eccentricity. The lunar eccentricity superimposes an apparent shaking
of the face of the Moon back and forth with the period of the lunar
orbit. Though the Moon does slightly change its rate of rotation
during the course of its orbit, most of this shaking is due to the
nonuniform motion of the Moon in its elliptical orbit. This
oscillation, called the ``optical libration of the Moon,''
allows us to see a bit more than half of the Moon's surface. The
longer-period oscillation induced by the kick is called the ``free
libration of the Moon.'' It is ``free'' because we are free to excite
it by choosing appropriate initial conditions. The mismatch of the
orientation of the Moon caused by the optical libration actually
produces a periodic torque on the Moon, which slightly speeds it up and
slows it down during every orbit. The resulting oscillation is
called the ``forced libration of the Moon,'' but it is too small to
see in this plot.
-
f with an orbital eccentricity of 0.05, near the current lunar
eccentricity. The lunar eccentricity superimposes an apparent shaking
of the face of the Moon back and forth with the period of the lunar
orbit. Though the Moon does slightly change its rate of rotation
during the course of its orbit, most of this shaking is due to the
nonuniform motion of the Moon in its elliptical orbit. This
oscillation, called the ``optical libration of the Moon,''
allows us to see a bit more than half of the Moon's surface. The
longer-period oscillation induced by the kick is called the ``free
libration of the Moon.'' It is ``free'' because we are free to excite
it by choosing appropriate initial conditions. The mismatch of the
orientation of the Moon caused by the optical libration actually
produces a periodic torque on the Moon, which slightly speeds it up and
slows it down during every orbit. The resulting oscillation is
called the ``forced libration of the Moon,'' but it is too small to
see in this plot.
The oscillation period of the free libration is easily calculated. We see that the eccentricity of the orbit does not substantially affect the period, so we consider the special case of zero eccentricity. In this case R = a, a constant, and f(t) = n t, where n is the orbital frequency (traditionally called the mean motion). The equation of motion becomes
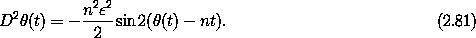
Let  (t) =
(t) =  (t) - n t, and consequently D
(t) - n t, and consequently D (t) = D
(t) = D (t)
- n, and D2
(t)
- n, and D2 = D2
= D2 . Substituting these, the equation
governing the evolution of
. Substituting these, the equation
governing the evolution of  is
is

For small deviations from synchronous rotation (small  ) this is
) this is

so we see that the small-amplitude oscillation frequency of  is n
is n . For the Moon,
. For the Moon,  is about 0.026, so the period
is about 1/0.026 orbit periods or about 40 lunar orbit periods, which
is what we observed.
is about 0.026, so the period
is about 1/0.026 orbit periods or about 40 lunar orbit periods, which
is what we observed.
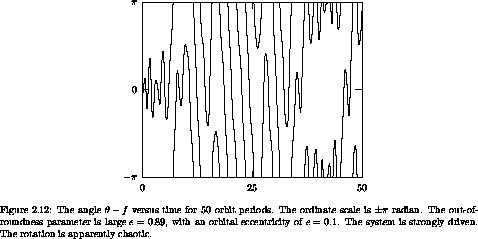
It is perhaps more fun to see what happens if the out-of-roundness
parameter is large. After our experience with the driven pendulum it
is no surprise that we find abundant chaos in the spin-orbit problem
when the system is strongly driven by having large  and
significant e. There is indeed one body in the solar system that
exhibits chaotic rotation -- Hyperion, a small satellite of Saturn.
Though our toy model is not adequate for a complete account of Hyperion,
we can show that it exhibits chaotic behavior for
parameters appropriate for Hyperion. We take
and
significant e. There is indeed one body in the solar system that
exhibits chaotic rotation -- Hyperion, a small satellite of Saturn.
Though our toy model is not adequate for a complete account of Hyperion,
we can show that it exhibits chaotic behavior for
parameters appropriate for Hyperion. We take  = 0.89 and
e = 0.1. Figure 2.12 shows
= 0.89 and
e = 0.1. Figure 2.12 shows  - f for
50 orbits, starting with
- f for
50 orbits, starting with  = 0 and
= 0 and  = 1.05. We see
that sometimes one face of the body oscillates facing the planet,
sometimes the other face oscillates facing the planet, and sometimes
the body rotates relative to the planet in either direction.
= 1.05. We see
that sometimes one face of the body oscillates facing the planet,
sometimes the other face oscillates facing the planet, and sometimes
the body rotates relative to the planet in either direction.
If we relax our restriction that the spin axis be fixed perpendicular to the orbit, then we find that the Moon maintains this orientation of the spin axis even if nudged a bit, but for Hyperion the spin axis almost immediately falls away from this configuration. The state in which Hyperion on average points one face to Saturn is dynamically unstable to chaotic tumbling. Observations of Hyperion have confirmed that it is chaotically tumbling.
15 The Legendre polynomials Pl may be obtained by expanding the expression (1 + y2 - 2 y x)-1/2 as a power series in y. The coefficient of yl is Pl(x). The first few Legendre polynomials are: P0(x) = 1, P1(x) = x, P2(x) = (3/2) x2 - (1/2), and so on. The rest satisfy the recurrence relation
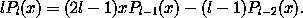
16 This approximate representation of the potential energy is sometimes called MacCullagh's formula.
17 Watch out, we just reused
 . It was also used as the constituent index.
. It was also used as the constituent index.
18 Traditionally, the point in the orbit at which the two bodies are closest is called the pericenter and the angle f is called the true anomaly.
19 The given potential energy differs from the actual potential
energy in that non-constant terms that do not depend on  and
consequently do not affect the evolution of
and
consequently do not affect the evolution of  have been
dropped.
have been
dropped.