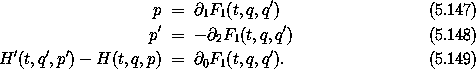
We have considered a number of properties of general canonical transformations without having a general method for coming up with them. Here we introduce the method of generating functions. The generating function is a real-valued function that compactly specifies a canonical transformation through its partial derivatives, as follows.
Consider a real-valued function F1(t, q, q') mapping configurations expressed in two coordinate systems to the reals. We will use F1 to construct a canonical transformation from one coordinate system to the other. We will show that the following relations among the coordinates, the momenta, and the Hamiltonians specify a canonical transformation:
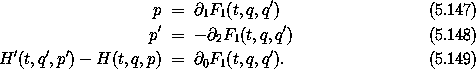
The transformation will then be explicitly given by solving for one
set of variables in terms of the others: To obtain the primed
variables in terms of the unprimed ones, let A be the inverse of
 1 F1 with respect to the third argument,
1 F1 with respect to the third argument,


Let B be the coordinate part of the phase-space transformation
q = B(t, q', p'). This B is an inverse function of  2
F1, satisfying
2
F1, satisfying


To put the transformation in explicit form requires that the inverse functions A and B exist.
We can use the above relations to verify that some given transformation from one set of phase-space coordinates (q, p) with Hamiltonian function H(t, q, p) to another set (q', p') with Hamiltonian function H'(t, q', p') is canonical by finding an F1(t, q, q') such that the above relations are satisfied. We can also use arbitrarily chosen generating functions of type F1 to generate new canonical transformations.
The polar-canonical transformation
(5.32) from coordinate and momentum
(x, px) to new coordinate and new momentum ( , I),
, I),

introduced earlier, is canonical. This can also be demonstrated by finding a suitable F1 generating function. The generating function satisfies a set of partial differential equations, (5.147) and (5.148):

Using relations (5.156) and (5.157), which specify the canonical transformation, equation (5.158) can be rewritten

which is easily integrated to yield
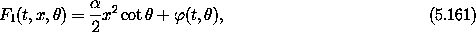
where  is some integration ``constant'' with respect to the
first integration. Substituting this form for F1 into the second
partial differential equation (5.159), we find
is some integration ``constant'' with respect to the
first integration. Substituting this form for F1 into the second
partial differential equation (5.159), we find
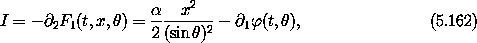
but we see that if we set  = 0 the desired relations are
recovered. So the generating function
= 0 the desired relations are
recovered. So the generating function

generates the polar-canonical transformation. This shows that this transformation is canonical.
We can prove directly that the transformation generated by F1 is canonical by showing that if Hamilton's equations are satisfied in one set of coordinates then they will be satisfied in the other set of coordinates. Let F1 take arguments (t, x, y). The relations among the coordinates are

and the Hamiltonians are related by
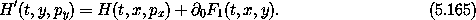
Substituting the generating function relations (5.164) into this equation, we have
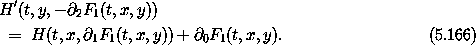
Take the partial derivatives of this equality of expressions with respect to the variables x and y:17
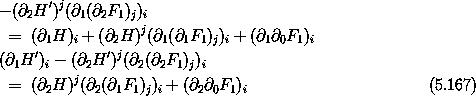
where the arguments are unambiguous and have been suppressed. On solution paths we can use Hamilton's equations for the (x, px) system to replace the partial derivatives of H with derivatives of x and px, obtaining
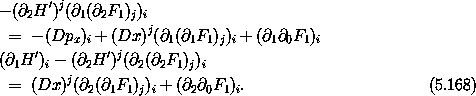
Now compute the derivative of px and py, from equations (5.164), along consistent paths:
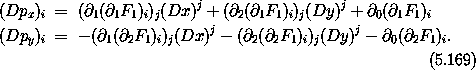
Substituting the first of these into the first of equations (5.168) yields
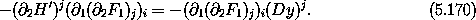
Note that ( 2 (
2 ( 1 F1)i)j = (
1 F1)i)j = ( 1
(
1
( 2 F1)j)i. Provided that
2 F1)j)i. Provided that  2
2  1 F1 is nonsingular,18
we have derived one of Hamilton's equations for the (y, py) system:
1 F1 is nonsingular,18
we have derived one of Hamilton's equations for the (y, py) system:


can be derived in a similar way. So the generating function relations indeed specify a canonical transformation.
What we have shown is that the transformation is canonical, which means that the equations of motion transform appropriately; we have not shown that the qp part of the transformation is symplectic. If the transformation is time independent then the Hamiltonians transform by composition, and in that circumstance we know that canonical implies symplectic.
Generating functions can be used to specify a canonical transformation by the prescription given above. We have shown that the generating function prescription gives a canonical transformation. Here we show how to get a generating function from a canonical transformation, and derive the generating function rules.
The generating function representation of canonical transformations can be derived from the Poincaré integral invariants. The outline is the following. We first show that, given a canonical transformation, the integral invariants imply the existence of a function of phase-space coordinates that can be written as a path-independent line integral. Then we show that partial derivatives of this function, represented in mixed coordinates, give the generating function relations between the old and new coordinates. We need to do this only for time-independent transformations because time-dependent transformations become time independent in the extended phase space.
Recall the result about integral invariants from section 5.3. There we found that

where R' is a two-dimensional region in (q', p') coordinates at
time t, and R = Ct(R') is the corresponding region in (q, p)
coordinates, and where  R indicates the boundary of the
region R. This holds for any region and its boundary. We will show
that this implies there is a function F(t, q', p') that can be
defined in terms of line integrals
R indicates the boundary of the
region R. This holds for any region and its boundary. We will show
that this implies there is a function F(t, q', p') that can be
defined in terms of line integrals
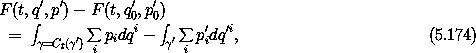
where  ' is a curve in phase-space coordinates that begins at
' is a curve in phase-space coordinates that begins at
 '(0) = (q'0, p'0) and ends at
'(0) = (q'0, p'0) and ends at  '(1) = (q', p'), and
'(1) = (q', p'), and
 is its image under Ct.
is its image under Ct.
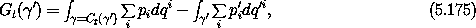
and let  '1 and
'1 and  '2 be two
paths with the same endpoints. Then
'2 be two
paths with the same endpoints. Then
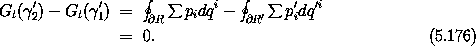
So the value of Gt( ') depends only on the endpoints of
') depends only on the endpoints of
 '.
'.

where  ' is any path from q'0, p'0 to q', p'.
Changing the initial point from q'0 p'0 to q'1 p'1 changes
the value of
' is any path from q'0, p'0 to q', p'.
Changing the initial point from q'0 p'0 to q'1 p'1 changes
the value of 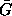 by a constant:
by a constant:
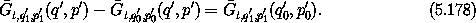
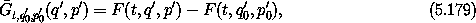
demonstrating equation (5.174).
The phase-space point (q, p) in unprimed variables corresponds to (q', p') in primed variables, at an arbitrary time t. Both p and q are determined given q' and p'. In general, given any two of these four quantities, we can solve for the other two. If we can solve for the momenta in terms of the positions we get a particular class of generating functions.19 We introduce the functions

that solve the transformation equations (t, q, p) = C(t, q', p') for the momenta in terms of the coordinates at a specified time. With these we introduce a function F1(t, q, q') such that

The function F1 has the same value as F but has different arguments. We will show that this F1 is in fact the generating function for canonical transformations introduced in section 5.6. Let's be explicit about the definition of F1 in terms of a line integral:
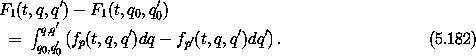
The two line integrals can be combined into this one because they are both expressed as integrals along a curve in (q, q').
We can use the path independence of F1 to compute the partial derivatives of F1 with respect to particular components and consequently derive the generating function relations for the momenta.20 So we conclude that


These are just the configuration and momentum parts of the generating function relations for canonical transformation. So starting with a canonical transformation, we can find a generating function that gives the coordinate-momentum part of the transformation through its derivatives.
Starting from a general canonical transformation, we have constructed an F1 generating function from which the canonical transformation may be rederived. So we expect there is a generating function for every canonical transformation.21
Point transformations were excluded from the previous argument because we could not deduce the momenta from the coordinates. However, a similar derivation allows us to make a generating function for this case. The integral invariants give us an equality of area integrals. There are other ways of writing the equality-of-areas relation (5.83) as a line integral. We can also write

The minus sign arises because by flipping the axes we are traversing the area in the opposite sense. Repeating the argument just given, we can define a function
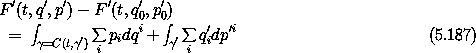
that is independent of the path  '. If we can solve for q'
and p in terms of q and p' we can define the functions
'. If we can solve for q'
and p in terms of q and p' we can define the functions

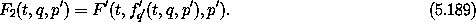
Then the canonical transformation is given as partial derivatives of F2:


For canonical transformations that can be described by both an F1 and an F2, there must be a relation between them. The alternate line integral expressions for the area integral are related. Consider the difference
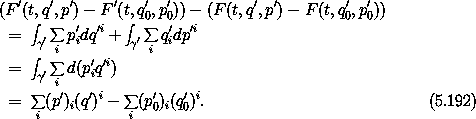
The functions F and F' are related by an integrated term


The generating functions F1 and F2 are related by a Legendre transform:
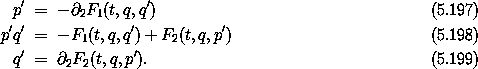
We have passive variables q and t:
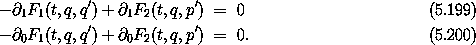
But p =  1 F1(t, q, q')
from the first transformation, so
1 F1(t, q, q')
from the first transformation, so

Furthermore, since H'(t, q', p') - H(t, q, p) =
 0 F1(t, q, q') we can conclude that
0 F1(t, q, q') we can conclude that
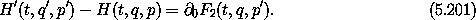
In summary, we have used F1-type generating functions to construct canonical transformations:
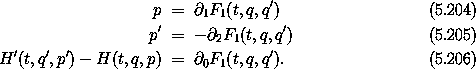
We can also represent canonical transformations with generating functions of the form F2(t, q, p'), where the third argument of F2 is the momentum in the primed system.22
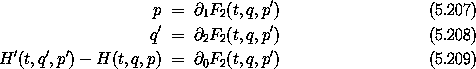
As in the F1 case, to put the transformation in explicit form requires that appropriate inverse functions be constructed to allow the solution of the equations.
Similarly, we can construct two other forms for generating functions, named mnemonically enough F3 and F4:
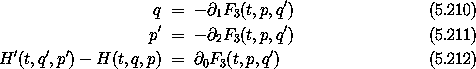
and
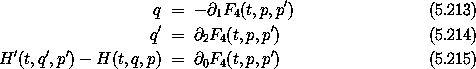
In every case, if the generating function does not depend explicitly on time then the Hamiltonians are obtained from one another purely by composition with the appropriate canonical transformation. If the generating function depends on time, then there are additional terms.
The generating functions presented treat the coordinates and momenta collectively. One could define more complicated generating functions for which the transformation of each degree of freedom is specified by generating functions of different types.
We can represent canonical transformations with mixed-variable generating functions. We can extend these to represent transformations in the extended phase space. Let F2 be a generating function with arguments (t, q, p'). Then, the corresponding Fe2 in the extended phase space can be taken to be
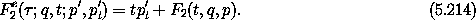
The relations between the coordinates and the momenta are the same as before. We also have
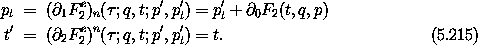
The first equation gives the relationship between the original Hamiltonians:
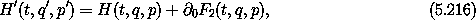
as required. We know that time-independent canonical transformations have symplectic qp part. The generating-function representation of a time-dependent transformation does not depend on the independent variable in the extended phase space. So, in extended phase space the qp part of the transformation, which includes the time and the momentum conjugate to time, is symplectic.
Point transformations can be represented in terms of a generating function of type F2. Equations (5.6), which define a canonical point transformation derived from a coordinate transformation F, are
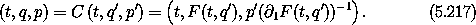
Let S be the inverse transformation of F with respect to the second argument

so that q' = S(t, F(t, q')). The momentum transformation that accompanies this coordinate transformation is

We can find the generating function F2 that gives this transformation by integrating equation (5.204) to get

Substituting this into equation (5.204), we get

We do not need the freedom provided by  , so we can set it equal
to zero:
, so we can set it equal
to zero:


So this F2 gives the canonical transformation of equations (5.217) and (5.218).
The canonical transformation for the coordinate transformation S is the inverse of the canonical transformation for F. By design F and S are inverses on the coordinate arguments. The identity function is q' = I(q') = S(t, F(t, q')). Differentiating yields


Using this, the relation between the momenta (5.222) is

showing that F2 gives a point transformation equivalent to the point transformation (5.216). So from this other point of view we see that the point transformation is canonical.
The F1 that corresponds to the F2 for a point transformation is
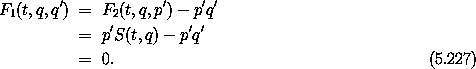
A commonly required point transformation is the transition between polar coordinates and rectangular coordinates:

Using the formula for the generating function of a point transformation just derived, we find:
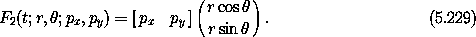
So the full transformation is derived:
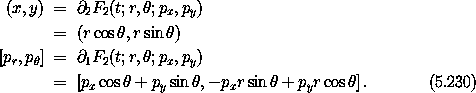
We can isolate the rectangular coordinates to one side of the transformation and the polar coordinates to the other:

So, interpreted in terms of Newtonian vectors, pr = 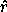 ·
·
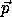 is the radial component of the linear momentum and p
is the radial component of the linear momentum and p =
||
=
|| 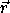 ×
× 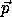 || is the magnitude of the angular
momentum. The point transformation is time independent, so the
Hamiltonian transforms by composition.
|| is the magnitude of the angular
momentum. The point transformation is time independent, so the
Hamiltonian transforms by composition.
A useful time-dependent point transformation is the transition to a rotating coordinate system. This is most easily accomplished in polar coordinates. Here we have

where 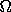 is the angular velocity of the rotating coordinate
system. The generating function is
is the angular velocity of the rotating coordinate
system. The generating function is
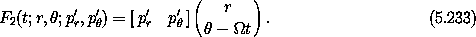
This yields the transformation equations

which show that the momenta are the same in both coordinate systems. However, here the Hamiltonian is not a simple composition:
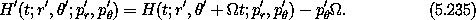
The Hamiltonians differ by the derivative of the generating function with respect to the time argument. In transforming to rotating coordinates, the values of the Hamiltonians differ by the product of the angular momentum and the angular velocity of the coordinate system. Notice that this addition to the Hamiltonian is the same as was found earlier (5.57).
Exercise 5.14. Rotating coordinates in extended phase space
In the extended phase space the time is one of the coordinates.
Carry out the transformation to rotating coordinates using an
F2-type generating function in the extended phase space. Compare
the Hamiltonian obtained by composition with the transformation to
Hamiltonian (5.234).
In this example we illustrate how canonical transformations can be used to eliminate some of the degrees of freedom, leaving an essential problem with fewer degrees of freedom.
Suppose that only certain combinations of the coordinates appear in the Hamiltonian. We make a canonical transformation to a new set of phase-space coordinates such that these combinations of the old phase-space coordinates are some of the new phase-space coordinates. We choose other independent combinations of the coordinates to complete the set. The advantage is that these other independent coordinates do not appear in the new Hamiltonian, so the momenta conjugate to them are conserved quantities.
Let's see how this idea enables us to reduce the problem of two gravitating bodies to the simpler problem of the relative motion of the two bodies, and in the process discover that the momentum of the center of mass is conserved.
Consider the motion of two masses m1 and m2, subject only to a mutual gravitational attraction described by the potential V(r). This problem has six degrees of freedom. The rectangular coordinates of the particles are x1 and x2, with conjugate momenta p1 and p2. Each of these is a structure of the three rectangular components. The distance between the particles is r = || x1 - x2 ||. The Hamiltonian for the two-body problem is
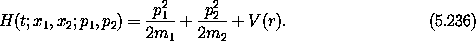
We do not need to specify V further at this point.
We note that the only linear combination of coordinates that appears in the Hamiltonian is x2 - x1. We choose new coordinates so that one of the new coordinates is this combination:

To complete the set of new coordinates we choose another to be some independent linear combination

where a and b are to be determined. We can use an F2-type generating function
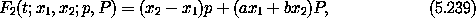
where p and P will be the new momenta conjugate to x and X, respectively. We deduce
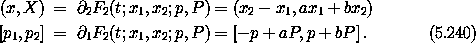
We can solve these for the new momenta:

The generating function is not time dependent so the new Hamiltonian is the old Hamiltonian composed with the transformation:
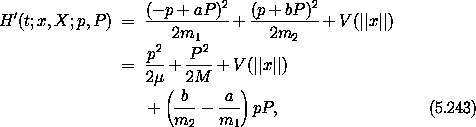


We recognize µ as the usual ``reduced mass.''
Notice that if the term proportional to p P were not present then the x and X degrees of freedom would not be coupled at all, and furthermore, the X part of the Hamiltonian would be just the Hamiltonian of a free particle, which is easy to solve. The condition that the ``cross terms'' disappear is


for any c. For a transformation to be defined c must be nonzero. So with this choice the Hamiltonian becomes
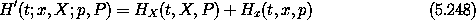


The reduced mass is the same as before, and now

Notice that, without further specifying c, the problem has been separated into the problem of determining the relative motion of the two masses, and the problem of the other degrees of freedom. We did not need a priori knowledge that the center of mass might be important; in fact, only for a particular choice of c = (m1 + m2)-1 does X become the center of mass.
It is often useful to compose a sequence of canonical transformations to make up the transformation we need for any particular mechanical problem. The transformations we have supplied are especially useful as components in these computations.
We will illustrate the use of canonical transformations to learn about planar motion in a central field. The strategy will be to consider perturbations of circular motion in the central field. The analysis will proceed by transforming to a rotating coordinate system that rides on a circular reference orbit, and then making approximations that restrict the analysis to orbits that differ from the circular orbit only slightly.
In rectangular coordinates we can easily write a Hamiltonian for the motion of a particle of mass m in a field defined by a potential energy that is a function only of the distance from the origin as follows:
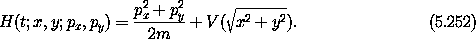
In this coordinate system Hamilton's equations are easy, and they are exactly what is needed to develop trajectories by numerical integration, but the expressions are not very illuminating:
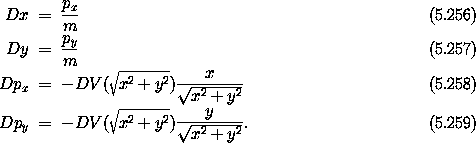
We can learn more by converting to polar coordinates centered on the source of our field:

This coordinate system explicitly incorporates the geometrical symmetry of the potential energy. Extending this coordinate transformation to a point transformation, we can write the new Hamiltonian as:
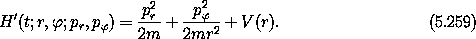
We can now write Hamilton's equations in these new coordinates, and they are much more illuminating than the equations expressed in rectangular coordinates:

We see that the angular momentum p is conserved, and we are
free to choose its constant value, so D
is conserved, and we are
free to choose its constant value, so D depends only on
r. We also see that we can establish a circular orbit at any radius
R0: we choose p
depends only on
r. We also see that we can establish a circular orbit at any radius
R0: we choose p = p
= p 0 so that p
0 so that p 02/(m R03) - DV(R0) = 0. This will ensure that Dpr = 0,
and thus Dr = 0. The (square of the) angular velocity of this
circular orbit is
02/(m R03) - DV(R0) = 0. This will ensure that Dpr = 0,
and thus Dr = 0. The (square of the) angular velocity of this
circular orbit is

It is instructive to consider how orbits that are close to the
circular orbit differ from the circular orbit. This is best done in
rotating coordinates in which a body moving in the circular orbit is a
stationary point at the origin. We can do this by converting to
coordinates that are
rotating with the circular orbit and centered on the orbiting body.
We proceed in three stages. First we will transform to a polar
coordinate system that is rotating at angular velocity 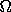 . Then
we will return to rectangular coordinates, and finally, we will shift
the coordinates so the origin is on the reference circular orbit.
. Then
we will return to rectangular coordinates, and finally, we will shift
the coordinates so the origin is on the reference circular orbit.
We start by examining the system in rotating polar coordinates. This is a time-dependent coordinate transformation:

Using equation (5.234), we can write the new Hamiltonian directly:
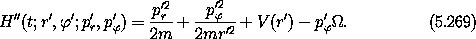
We see that H'' is not time dependent, and therefore it is conserved, but it is not energy. Energy is not conserved in the moving coordinate system, but what is conserved here is a new quantity that combines the energy with the product of the angular momentum of the particle in the new coordinate and the angular velocity of the coordinate system. We will want to keep track of this term.
Next, we return to rectangular coordinates, but they are rotating with the reference circular orbit:
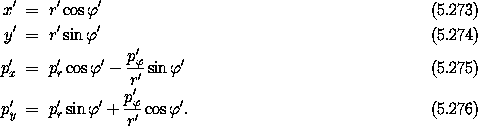
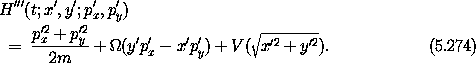
With one more quick manipulation we shift the coordinate system so
that the origin is out on our circular orbit. We define new
rectangular coordinates  and
and  with the following
simple canonical transformation of coordinates and momenta:
with the following
simple canonical transformation of coordinates and momenta:

In this final coordinate system the Hamiltonian is
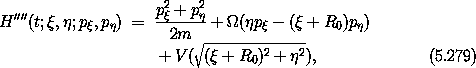
and Hamilton's equations are uselessly complicated, but the next step is to consider only
trajectories for which the coordinates  and
and  are small
compared with R0. Under this assumption we will be able to
construct approximate equations of motion for these trajectories that
are linear in the coordinates, thus yielding simple analyzable motion.
To this point we have made no approximations. The
equations above are perfectly accurate for any trajectories in a
central field.
are small
compared with R0. Under this assumption we will be able to
construct approximate equations of motion for these trajectories that
are linear in the coordinates, thus yielding simple analyzable motion.
To this point we have made no approximations. The
equations above are perfectly accurate for any trajectories in a
central field.
The idea is to expand the potential-energy term in the Hamiltonian as a series and to discard any term higher than second-order in the coordinates, thus giving us first-order-accurate Hamilton's equations:
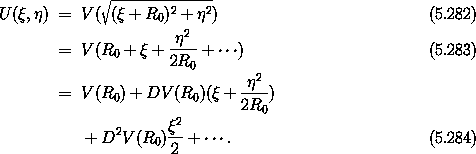
So the (negated) generalized forces are
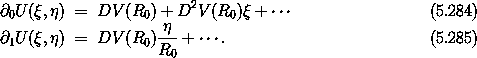
With this expansion we obtain the linearized Hamilton's equations:
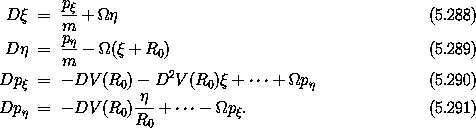
Of course, once we have linear equations we know how to solve them
exactly. Because the linearized Hamiltonian is conserved we cannot get
exponential expansion or collapse, so the possible solutions are
quite limited. It is instructive to convert these equations into a
second-order system. We use 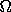 2 = DV(R0)/(m R0),
equation (5.263), to
eliminate the DV terms:
2 = DV(R0)/(m R0),
equation (5.263), to
eliminate the DV terms:
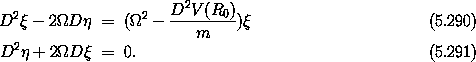


Thus we have a simple harmonic oscillator with frequency  as
one of the components of the solution. The general solution has
three parts:
as
one of the components of the solution. The general solution has
three parts:
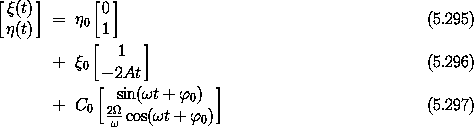

The constants  0,
0,  0, C0, and
0, C0, and  0 are determined
by the initial conditions. If C0 = 0, the particle of interest is on
a circular trajectory, but not necessarily the same one as the
reference trajectory. If C0 = 0 and
0 are determined
by the initial conditions. If C0 = 0, the particle of interest is on
a circular trajectory, but not necessarily the same one as the
reference trajectory. If C0 = 0 and  0 = 0, we have a ``fellow
traveler,'' a particle in the same circular orbit as the reference
orbit but with different phase. If C0 = 0 and
0 = 0, we have a ``fellow
traveler,'' a particle in the same circular orbit as the reference
orbit but with different phase. If C0 = 0 and  0 = 0, we have a
particle in a circular orbit that is interior or exterior to the
reference orbit and shearing away from the reference orbit. The
shearing is due to the fact that the angular velocity for a circular
orbit varies with the radius. The constant A gives the rate of
shearing at each radius. If both
0 = 0, we have a
particle in a circular orbit that is interior or exterior to the
reference orbit and shearing away from the reference orbit. The
shearing is due to the fact that the angular velocity for a circular
orbit varies with the radius. The constant A gives the rate of
shearing at each radius. If both  0 = 0 and
0 = 0 and  0 = 0 but C0
neq 0, then we have ``epicyclic motion''. A particle in a nearly
circular orbit may be seen to move in an ellipse around the circular
reference orbit. The ellipse will be elongated in the direction of
circular motion by the factor 2
0 = 0 but C0
neq 0, then we have ``epicyclic motion''. A particle in a nearly
circular orbit may be seen to move in an ellipse around the circular
reference orbit. The ellipse will be elongated in the direction of
circular motion by the factor 2 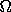 /
/ and it will
rotate in the direction opposite to the direction of the circular motion.
The initial phase of the epicycle is
and it will
rotate in the direction opposite to the direction of the circular motion.
The initial phase of the epicycle is  0. Of course, any
combination of these solutions may exist.
0. Of course, any
combination of these solutions may exist.
The epicyclic frequency  and the shearing rate A are
determined by the force law (the radial derivative of the potential
energy). For a force law proportional to a power of the radius,
and the shearing rate A are
determined by the force law (the radial derivative of the potential
energy). For a force law proportional to a power of the radius,

the epicyclic frequency is related to the orbital frequency by


For a few particular integer force laws we see:
|
We can get some insight into the kinds of orbits produced by
the epicyclic approximation by looking at a few examples. For some
force laws we have integer ratios of epicyclic frequency to orbital
frequency. In those cases we have closed orbits. For an
inverse-square force law (n = 3) we get elliptical orbits with the center of
the field at a focus of the ellipse. Figure 5.3 shows
how an approximation to such an orbit can be constructed by
superposition of the motion on an elliptical epicycle with the motion
of the same frequency on a circle. If the force is proportional to
the radius (n = 0) we get a two-dimensional harmonic oscillator. Here the
epicyclic frequency is twice the orbital frequency.
Figure 5.4 shows how this yields elliptical orbits
that are centered on the source of the central force. An orbit is
closed when  /
/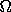 is a rational
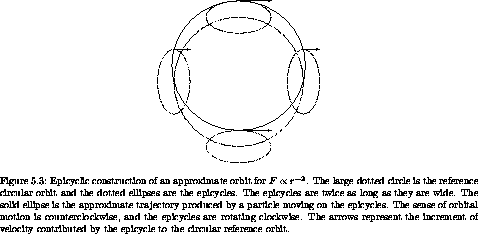
fraction. If the force is proportional to the - 3/4 power of the
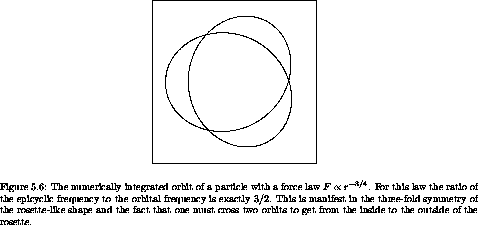
radius, the epicyclic frequency is 3/2 the orbital frequency. This
yields the three-lobed pattern seen in
figure 5.5. For other force laws the orbits predicted
by this analysis are multi-lobed patterns produced by precessing
approximate ellipses. Most of the cases have incommensurate epicyclic
and orbital frequencies, leading to orbits that do not close in finite
time.
is a rational
fraction. If the force is proportional to the - 3/4 power of the
radius, the epicyclic frequency is 3/2 the orbital frequency. This
yields the three-lobed pattern seen in
figure 5.5. For other force laws the orbits predicted
by this analysis are multi-lobed patterns produced by precessing
approximate ellipses. Most of the cases have incommensurate epicyclic
and orbital frequencies, leading to orbits that do not close in finite
time.
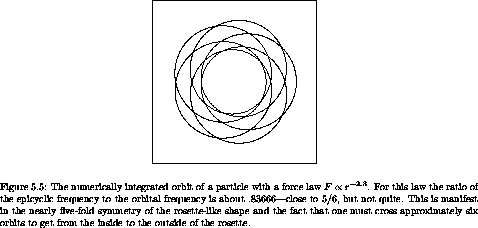
The epicyclic approximation gives a very good idea of what actual orbits look like. Figure 5.6, drawn by numerical integration of the orbit produced by integrating the original rectangular equations of motion for a particle in the field, shows the rosette-type picture characteristic of incommensurate epicyclic and orbital frequencies for an F = - r-2.3 force law.
We can directly compare a numerically integrated system with one of our epicyclic approximations. For example, the result of numerically integrating our F propto r-3/4 system is very similar to the picture we obtained by epicycles. (See figure 5.7 and compare it with figure 5.5.)
Exercise 5.15. Collapsing orbits
What exactly happens as the force law becomes steeper? Investigate
this by sketching the contours of the Hamiltonian in r, pr space
for various values of the force-law exponent, n. For what values of
n are there stable circular orbits? In the case that there are no
stable circular orbits, what happens to circular and other noncircular
orbits? How are these results consistent with Liouville's theorem and
the nonexistence of attractors in Hamiltonian systems?
The addition of a total time derivative to a Lagrangian leads to the same Lagrange equations. However, the two Lagrangians have different momenta, and they lead to different Hamilton's equations. Here we find out how to represent the corresponding canonical transformation with a generating function.
Let's restate the result about total time derivatives and Lagrangians from the first chapter. Consider some function G(t, q) of time and coordinates. We have shown that if L and L' are related by
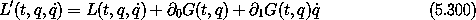
then the Lagrange equations of motion are the same. The generalized coordinates used in the two Lagrangians are the same, but the momenta conjugate to the coordinates are different. In the usual way, define


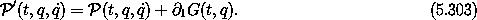
Evaluated on a trajectory, we have

This transformation is a special case of an F2-type transformation. Let

then the associated transformation is
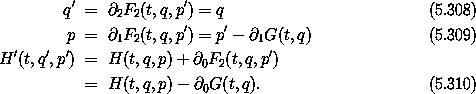
Explicitly, the new Hamiltonian is
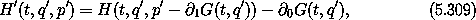
where we have used the fact that q = q'. The transformation is interesting in that the coordinate transformation is the identity transformation, but the new and old momenta are not the same, even in the case in which G has no explicit time dependence. Suppose we have a Hamiltonian of the form

then the transformed Hamiltonian is
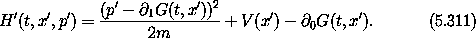
We see that this transformation may be used to modify terms in the Hamiltonian that are linear in the momenta. Starting from H, the transformation introduces linear momentum terms; starting from H', the transformation eliminates the linear terms.
We illustrate the use of this transformation with the driven pendulum. The Hamiltonian for the driven pendulum derived from the T - V Lagrangian (see section 1.6.2) is
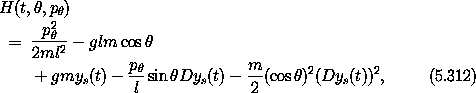
where ys is the drive function. The Hamiltonian is rather messy, and includes a term that is linear in the angular momentum with a coefficient that depends on both the angular coordinate and the time. Let's see what happens if we apply our transformation to the problem to eliminate the linear term. We can identify the transformation function G by requiring that the linear term in momentum be killed:


and the transformed Hamiltonian is
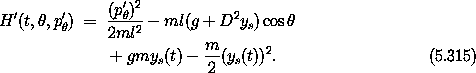
Dropping the last two terms, which do not affect the equations of motion, we find
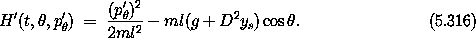
So we have found, by a straightforward canonical transformation, a Hamiltonian for the driven pendulum with the rather simple form of a pendulum with gravitational acceleration that is modified by the acceleration of the pivot. It is, in fact, the Hamiltonian that corresponds to the alternate form of the Lagrangian for the driven pendulum we found earlier by inspection (see equation 1.120). Here the derivation is by a simple canonical transformation, motivated by a desire to eliminate unwanted terms that are linear in the momentum.
Exercise 5.16. Construction of generating functions
Suppose that canonical transformations Ca and Cb are generated by F1-type generating functions F1a and F1b.
a. Show that the generating function for the inverse transformation of Ca is - F1a.
b. Show that the generating function for the composition transformation Ca o Cb is F1a + F1b, using the fact that the generating function does not depend on the intermediate point.
Exercise 5.17. Linear canonical transformations
We consider systems with two degrees of freedom and transformations
for which the Hamiltonian transforms by composition.
a. Consider the linear canonical transformations that are generated by
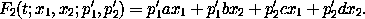
Show that these transformations are just the point transformations, and that the corresponding F1 is zero.
b. Other linear canonical transformations can be generated by
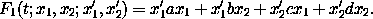
Surely we can make even more generators by constructing F3- and F4-type transformations analogously. Are all of the linear canonical transformations obtainable in this way? If not, show one that cannot be so generated.
c. Can all linear canonical transformations be generated by compositions of transformations generated by the functions shown in parts a and b above?
d. How many independent parameters are necessary to specify all possible linear canonical transformations for systems with two degrees of freedom?
Exercise 5.18. Integral invariants
Consider the linear canonical transformation for a system with two degrees of freedom generated by the function:
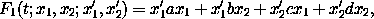
and the general parallelogram with a vertex at the origin and with adjacent sides starting at the origin and extending to the phase-space points (x1a, x2a, p1a, p2a) and (x1b, x2b, p1b, p2b).
a. Find the area of the given parallelogram and the area of the target parallelogram under the canonical transformation. Notice that the area of the parallelogram is not preserved.
b. Find the areas of the projections of the given parallelogram and the areas of the projections of the target under canonical transformation. Show that the sum of the areas of the projections on the action-like planes is preserved.
Exercise 5.19. Standard-map generating function
Find a generating function for the standard map (see
exercise 5.5).
Exercise 5.20. An incorrect derivation
The following is an incorrect derivation of the rules for the
generating function. As you read it, try to find the bug. Write an
essay on this subject. What is actually the problem?
Let L and L' be the Lagrangians expressed in two coordinate
systems for which the path is q and q', respectively. We
further assume that the values of L and L' on the path differ
by the time derivative of a function of the configuration and time
evaluated on the path. This function can be written in terms of the
path expressed in terms of both sets of coordinates. Consider the
function F1(t, q, q'), and its value on the path
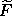 1(t) = F1(t, q(t), q'(t)) at time t. The time
derivative of
1(t) = F1(t, q(t), q'(t)) at time t. The time
derivative of 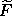 1 is
1 is
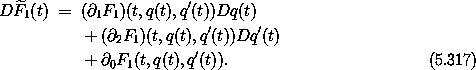
The relation between the Lagrangians is therefore
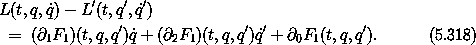
Now rewrite the Lagrangians in terms of the Hamiltonians
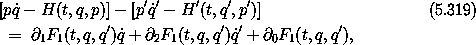
where p is determined by t, q,  , and the Lagrangian
L. Similar relations hold for the primed functions. Let's collect
terms:
, and the Lagrangian
L. Similar relations hold for the primed functions. Let's collect
terms:
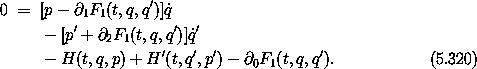
If the relations (5.147-5.149) hold, then each of these lines is independently zero, apparently verifying that the Lagrangians differ by a total time derivative. If this were true then the equations of motion would be preserved and the transformation would have been shown to be canonical.23
17 Here we use indices to select particular components of
structured objects. If an index symbol appears both as a superscript
and as a subscript in an expression, the value of the expression is
the sum over all possible values of the index symbol of the designated
components (Einstein summation convention). Thus, for example, if
 and p are of dimension n then the indicated product pi
and p are of dimension n then the indicated product pi
 i is to be interpreted as
i is to be interpreted as  i=0n-1 pi
i=0n-1 pi  i
.
i
.
18 A structure is nonsingular if the determinant of the matrix representation of the structure is nonzero.
19 Point transformations are not in this class: we cannot solve for the momenta in terms of the positions for point transformations, because for a point transformation the primed and unprimed coordinates can be deduced from each other, so there is not enough information in the coordinates to deduce the momenta.
20 Let F be defined as the path-independent line integral
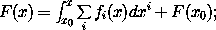
then
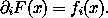
The partial derivatives of F do not depend on the constant point x0 or the path from x0 to x, so we can choose a path that is convenient for evaluating the partial derivative. Let
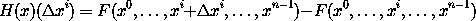
The partial derivative of F with respect to the ith component of F is
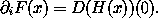
The function H is defined by the line integral
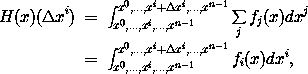
where the second line follows because the line integral is along the coordinate direction xi. This is now an ordinary integral, so
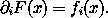
21 There may be some singular cases and topological problems that prevent this from being rigorously true.
22 The various generating functions are traditionally known by the names F1, F2, F3, and F4. Please don't blame us.
23 Many texts further muddy the matter by introducing an
unjustified independence argument here: they argue that because
 and
and 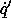 are independent the
relations (5.147-5.149) must hold. This is silly,
because p and p' are functions of
are independent the
relations (5.147-5.149) must hold. This is silly,
because p and p' are functions of  and
and 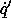 ,
respectively, so there are implied dependencies of the velocities in
many places, and thus it is unjustified to separately set pieces of this
equation to zero. However, notwithstanding this problem, the
derivation of the fact that the transformation is canonical is
fallacious.
,
respectively, so there are implied dependencies of the velocities in
many places, and thus it is unjustified to separately set pieces of this
equation to zero. However, notwithstanding this problem, the
derivation of the fact that the transformation is canonical is
fallacious.