
We started with an integrable system, where there are invariant curves. Do any invariant curves survive if a perturbation is added?
The Poincaré-Birkhoff construction for twist maps shows that invariant curves with rational rotation number typically do not survive perturbation. Upon perturbation the invariant curves with rational rotation numbers are replaced by an alternating sequence of stable and unstable periodic orbits. So if there are invariant curves that survive perturbation they must have irrational rotation numbers.
The perturbed system has chains of alternating stable and unstable fixed points for every rational rotation number. Each stable fixed point is surrounded by an island that occupies some region of the section. Each irrational is arbitrarily close to a rational, so it is not obvious that any invariant curve can survive an arbitrarily small perturbation.
Nevertheless, the Kolmogorov-Arnold-Moser (KAM) theorem proves that invariant curves do exist if the perturbation is small enough that the perturbed problem is ``close enough'' to an integrable problem, and if the rotation number is ``irrational enough.'' We will not prove this theorem here. Instead we will develop methods for finding particular invariant curves.
Stable periodic orbits have a stable island surrounding them on the surface of section. The largest islands are associated with rationals with small denominators. In general, the size of the island is limited to a size that decreases as the denominator increases. These islands are a local indication of the effect of the perturbation. Similarly, the chaotic zones appear near unstable periodic orbits and their homoclinic tangles. The homoclinic tangle is a continuous curve so it cannot cross an invariant curve, which is also continuous. If we are looking for invariant curves that persist upon perturbation, we would be wise to avoid regions of phase space where the islands or homoclinic tangles are major features.
The Poincaré-Birkhoff islands are ordered by rotation number. Because of the twist condition, the rotation number is monotonic in the momentum of the unperturbed problem. If there is an invariant curve with a given rotation number, it is sandwiched between island chains associated with rational rotation numbers. The rotation number of the invariant curve must be between the rotation numbers of the island chains on either side of it.
The fact that the size of the islands decreases with the size of the denominator suggests that invariant curves with rotation numbers for which nearby rationals require large denominators are the most likely to exist. So we will begin our search for invariant curves by examining rotation numbers that are not near rationals with small denominators.
Any irrational can be approximated by a sequence of rationals, and for each of these rationals we expect there to be stable and unstable periodic orbits with stable islands and homoclinic tangles. An invariant curve for a given rotation number has the best chance of surviving if the size of the islands associated with the each rational approximation is smaller than the separation of the islands from the invariant curve with that rotation number.
For any particular size denominator, the best rational approximation to an irrational number is given by an initial segment of a simple continued fraction. If the approximating continued fraction converges slowly to the irrational number, then that number is not near rationals with small denominators. Thus, we will look for invariant curves with rotation numbers that have slowly converging continued-fraction approximations. The continued fractions that converge most slowly have tails that are all one. Such a number is called a golden number. For example, the golden ratio,

is just such a number.
Invariant curves, if there are any, are characterized by a particular rotation number. Points on the invariant curve map to points on the invariant curve. Neighboring points map to neighboring points, preserving the order.
On the section for the unperturbed integrable system, the angle
between successive section points is constant: 
 = 2
= 2 
 (J) for rotation number
(J) for rotation number  (J). This map of the circle onto itself
with constant angular step we call a uniform circle map.
(J). This map of the circle onto itself
with constant angular step we call a uniform circle map.
For a given rotation number points on the section are laid down in a
particular order characteristic of the rotation number only. As a
perturbation is turned on, the invariant curve with a particular
rotation number will be distorted and the angle between successive
points will no longer be constant. All that is required to have a
particular rotation number is that the average change in angle
be 
 . Nevertheless, the ordering of the points on the
surface of section is preserved, and is characteristic of the rotation
number.
. Nevertheless, the ordering of the points on the
surface of section is preserved, and is characteristic of the rotation
number.
The sequence of points on the surface of section for an invariant curve with a given rotation number must have a particular order. We can use this fact to find the invariant curve. At a specified angle we perform a bisection search for the momentum that lies on the invariant curve. We can tell whether the initial point is on the desired invariant curve or which side of the invariant curve it is on by evolving a candidate initial point with both the perturbed map and the uniform circle map and comparing the ordering of the sequences of points that are generated.
A program to implement this plan of attack is14
(define (find-invariant-curve the-map rn theta0 Jmin Jmax eps)
(bisect (lambda (J) (which-way? rn theta0 J the-map))
Jmin Jmax eps))
However, we need to be able to determine which way to change the initial momentum to approach the required rotation number.
We can evolve the orbits for both maps, producing streams of points that appear on the section. (The momentum value of the uniform circle map is superfluous.) Each orbit stream is transduced into a stream of positive integers. The integers give the number of points in the stream that have been determined to have smaller values of the angle than the current point. The streams of integers are then compared until a discrepancy is found. The first discrepancy is used to compare the rotation numbers of the two orbits, to determine which orbit has smaller rotation number:
(define (which-way? rn theta0 J0 the-map)
(compare-streams
(position-stream theta0
(orbit-stream the-map theta0 J0)
'())
(position-stream theta0
(orbit-stream (uniform-circle-map rn)
theta0 J0)
'())
0))
The maps are evolved and built into a stream by a simple recursive procedure. The maps are represented in the same way as in section 3.6.2:
(define (orbit-stream the-map x y)
(cons-stream (list x y)
(the-map x y
(lambda (nx ny)
(orbit-stream the-map nx ny))
(lambda () 'fail))))
The uniform-circle-map is a simple map that has a uniformly progressing angle with constant momentum:
(define (uniform-circle-map rotation-number)
(let ((delta-theta (* :2pi rotation-number)))
(lambda (theta y result fail)
(result ((principal-value :2pi) (+ theta delta-theta))
y))))
The procedure position-stream produces a stream of index positions. It maintains an ordered list of angle values, and as each new angle is added to the list it adds the position index to the stream. A principal value is applied to the angle to bring it to a uniform range specified:
(define (position-stream cut orbit list)
(insert! ((principal-value cut) (car (head orbit)))
list
(lambda (nlist position)
(cons-stream
position
(position-stream cut (tail orbit) nlist)))))
Given a new element x to be inserted into an ordered set set, the procedure insert! calls its continuation with the updated set and the index that was used to insert the new element.15
The streams of indices are compared with compare-streams:
(define (compare-streams s1 s2 count)
(if (= (head s1) (head s2))
(compare-streams (tail s1) (tail s2) (+ count 1))
((principal-range count) (- (head s2) (head s1)))))
The count is used to keep track of how many points we have already entered into the circle. When there is a discrepancy between the indices, it means that one stream has begun to lead the other. The principal-range procedure is used to determine which is the leader.16 This is analogous to using the principal value to determine the direction from one angle to another on a circle.
Once we have created this mess we can use it to find the initial momentum (for a given initial angle) for an invariant curve with a given rotation number. We search the standard map for an invariant curve with a golden rotation number:17
(find-invariant-curve (standard-map 0.95)
(- 1 (/ 1 golden-ratio))
0.0
2.0
2.2
1e-5)
;Value: 2.114462280273437
This algorithm, although correct, has terrible performance. The problem is that each orbit builds a table of length the number of points examined, and each insertion of a new point scans that table sequentially, thus making a process that grows in time as the square of the number of points examined and in space as the number of points examined.
However, we observe that as ordering inconsistencies are found the angles are usually near the initial angle. We can make use of this to simplify the algorithm. Instead of keeping track of the whole list of angles, we can keep track of a small list of angles near the initial angle. In fact, keeping track of the nearest angle on either side of the initial angle works well.
Here is the complete replacement for
the which-way? procedure and its helpers. The procedure is
implemented as a simple loop with state variables for the two orbits
and the endpoints of the intervals. The z variables keep track
of the angle of the uniform circle map; the x variables keep track of
the angle of the map under study. The y variable is the
momentum for the map under study. On each iteration we determine
if the angle of the uniform circle map is in the interval of interest below or
above the initial angle. If it is in neither interval then the map is
further iterated. However, if it is in the region of interest then we
check to see if the angle of the other map is in the corresponding
interval. If so, the intervals for the uniform circle map and the other map
are narrowed and the iteration proceeds. If the angle is not in the
required interval, a discrepancy is noted and the sign of the
discrepancy is reported. For this process to make sense the
differences between the angles for successive iterations of both maps
must be less than  .
.
(define (which-way? rotation-number x0 y0 the-map)
(let ((pv (principal-value (+ x0 pi))))
(let lp ((z x0) (zmin (- x0 :2pi)) (zmax (+ x0 :2pi))
(x x0) (xmin (- x0 :2pi)) (xmax (+ x0 :2pi))
(y y0))
(let ((nz (pv (+ z (* :2pi rotation-number)))))
(the-map x y
(lambda (nx ny)
(let ((nx (pv nx)))
(cond ((< x0 z zmax)
(if (< x0 x xmax)
(lp nz zmin z nx xmin x ny)
(if (> x xmax) 1 -1)))
((< zmin z x0)
(if (< xmin x x0)
(lp nz z zmax nx x xmax ny)
(if (< x xmin) -1 1)))
(else
(lp nz zmin zmax nx xmin xmax ny)))))
(lambda ()
(error "Map failed" x y)))))))
With this method of comparing rotation numbers we can find the initial conditions for an invariant curve to high precision:
(find-invariant-curve (standard-map 0.95)
(- 1 (/ 1 golden-ratio))
0.0
2.0
2.2
1e-16)
;Value: 2.1144605494391726
Using initial conditions computed in this way, we can produce the invariant curve (see figure 4.20). If we expand the putative invariant curve it should remain a curve for all magnifications -- it should show no sign of chaotic fuzziness (see figure 4.21).
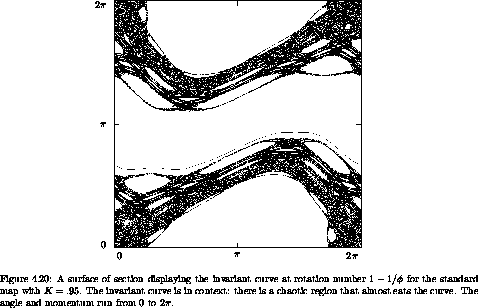
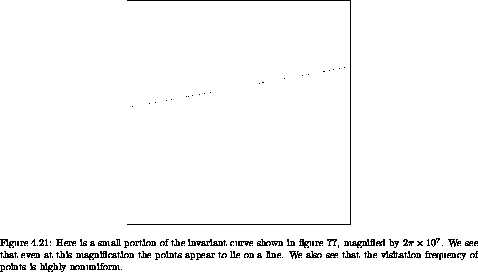
Exercise 4.8. Invariant curves in the standard map
Find an invariant curve of the standard
map with a different golden rotation number.
Expand it to show that it retains the features of a curve at
high magnification.
As can be seen in figure 4.21, the points on an invariant curve are not uniformly visited, unlike the picture we would get plotting the angles for the uniform circle map. This is because an interval may be expanded or compressed when mapped. We can compute the relative probability density for visitation of each angle on the invariant curve. A crude way to obtain this result is to count the number of points that fall into equal incremental angle bins. It is more effective to use the linear variational map constructed from the map being investigated to compute the change in incremental angle from one point to its successor. Since all of the points in a small interval around the source point are mapped to points (in the same order) in a small interval around the target point, the relative probability density at a point is inversely proportional to the size of the incremental interval around that point. In order to get this started we need a good estimate of the initial slope for the invariant curve. We can estimate the slope by a difference quotient of the momentum and angle increments for the interval that we used to refine the momentum of the invariant curve with a given rotation number.
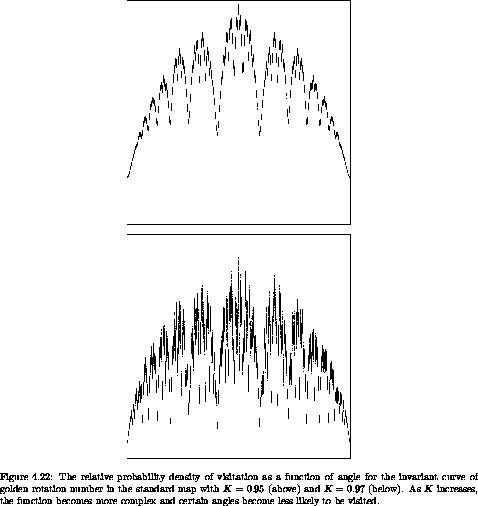
Figures 4.22 and 4.23 show the relative probability density of visitation as a function of angle for the invariant curve of golden rotation number in the standard map for three different values of the parameter K. As K increases, certain angles become less likely. Near K = 0.971635406 some angles are never visited. But the invariant curve must be continuous. Thus it appears that for larger K the invariant curve with this rotation number will not exist. Indeed, if the invariant set persists with the given rotation number it will have an infinite number of holes (because it has an irrational rotation number). Such a set is sometimes called a cantorus.

14 This method depends on the assumptions that Jmin and Jmax bracket the actual momentum, and that the rotation number is sufficiently continuous in momentum in that region.
15 The insert procedure is ugly:
(define (insert! x set cont)
(cond ((null? set) (cont (list x) 1))
((< x (car set)) (cont (cons x set) 0))
(else (let lp ((i 1) (lst set))
(cond ((null? (cdr lst))
(set-cdr! lst (cons x (cdr lst)))
(cont set i))
((< x (cadr lst))
(set-cdr! lst (cons x (cdr lst)))
(cont set i))
(else (lp (+ i 1) (cdr lst))))))))
16 The principal-range procedure is implemented as follows:
(define ((principal-range period) index)
(let ((t (- index (* period (floor (/ index period))))))
(if (< t (/ period 2.))
t
(- t period))))
17 There is no invariant curve in the standard map that has rotation number phi = 1.618.... However, 1 - 1/phi has the same continued-fraction tail as phi and there are rotation numbers of this size in the standard map.