A point transformation is a canonical transformation that extends a possibly time-dependent transformation of the configuration coordinates to a phase-space transformation. For example, one might want to reexpress motion in terms of polar coordinates, given a description in terms of rectangular coordinates. In order to extend a transformation of the configuration coordinates to a phase-space transformation we must specify how the momenta and Hamiltonian are transformed.
We have already seen how configuration transformations can be carried out in the Lagrangian formulation (see section 1.6.1). In that case, we found that if the Lagrangian transforms by composition with the coordinate transformation, then the Lagrange equations are equivalent.
Lagrangians that differ by the addition of a total time derivative are equivalent, but have different momenta conjugate to the generalized coordinates. So there is more than one way to make a canonical extension of a coordinate transformation.
Here, we find the particular canonical extension of a coordinate transformation for which the Lagrangians transform by composition with the transformation, with no extra total time derivative terms added to the Lagrangian.
Let L be a Lagrangian for a system. Consider the coordinate transformation q = F(t, q'). The velocities transform by
We can obtain a Lagrangian in the transformed coordinates by composition L'(t, q', v') = L(t, q, v):
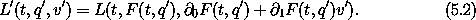
The momentum conjugate to q' is
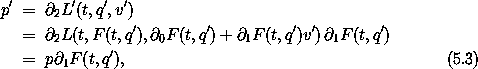
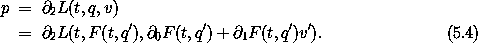
We can collect these results to define a canonical phase-space transformation C:2
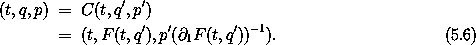
The Hamiltonian is obtained by the Legendre transform
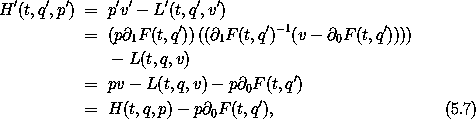
using relations (5.1) and (5.5) in the second step. Fully expressed in terms of the transformed coordinates and momenta, the transformed Hamiltonian is
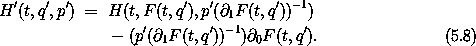
The Hamiltonians H' and H are equivalent because L and L' have the same value for a given dynamical state and so have the same paths of stationary action. In general H and H' do not have the same values for a given dynamical state, but differ by a term that depends on the coordinate transformation.
For time-independent transformations,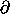 
0 F = 0, there are a
number of simplifications. The relationship of the velocities
(5.1) becomes
Comparing this to the relation (5.5) between the momenta, we see that in this case the momenta transform ``oppositely'' to the velocities3
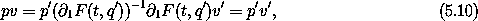
so the product of the momenta and the velocities is not changed by the transformation. This, combined with the fact that by construction L(t, q, v) = L'(t, q', v'), shows that
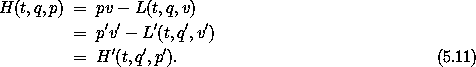
For time-independent coordinate transformations the Hamiltonian transforms by composition with the associated phase-space transformation. We can also see this from the general relationship (5.7) between the Hamiltonians.
The procedure F->CT takes a procedure F implementing a transformation of configuration coordinates and returns a procedure implementing a transformation of phase-space coordinates:
(define ((F->CT F) H-state)
(up (time H-state)
(F H-state)
(* (momentum H-state)
(invert (((partial 1) F) H-state)))))
Consider a particle moving in a central field. In rectangular coordinates a Hamiltonian is
(define ((H-central m V) H-state)
(let ((x (coordinate H-state))
(p (momentum H-state)))
(+ (/ (square p) (* 2 m))
(V (sqrt (square x))))))
Let's look at this Hamiltonian in polar coordinates. The phase-space transformation is obtained by applying F->CT to the procedure p->r that takes a time and a polar tuple and returns a tuple of rectangular coordinates (see section 1.6.1). The transformation is time independent so the Hamiltonian transforms by composition. In polar coordinates the Hamiltonian is
(show-expression
((compose (H-central 'm (literal-function 'V))
(F->CT p->r))
(up 't
(up 'r 'phi)
(down 'p_r 'p_phi))))
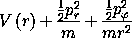
There are three terms. There is the potential energy, which depends
on the radius, there is the kinetic energy due to radial motion, and
there is the kinetic energy due to tangential motion. As expected,
the angle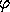 
does not appear and thus the angular momentum is a
conserved quantity. By going to polar coordinates we have decoupled
one of the two degrees of freedom in the problem.
Let q and q' be rectangular coordinates that are related by a rotation R: q = R q'. The Lagrangian for the system is L(t, q, v) = (1/2) m v2 - V(q). Find the corresponding phase-space transformation C. Compare the transformation equations for the rectangular components of the momenta to those for the rectangular components of the velocities. Are you surprised, considering equation (5.10)?
1 Solving for p in terms of p' involves multiplying
equation (5.3) on the right by (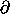1
F(t, q'))-1. This inverse is the structure that when multiplying
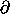1 F(t, q') on the right gives an identity structure.
Structures representing linear transformations may be represented in
terms of matrices. In this case, the matrix representation of the
inverse structure is the inverse of the matrix representing the
given structure.
2 In chapter 1 the transformation C takes a local tuple in one coordinate system and gives a local tuple in another coordinate system. In this chapter C is a phase-space transformation.
3 The velocities and the momenta are dual geometric objects with respect to time-independent point transformations. The velocities comprise a vector field on the configuration manifold, and the momenta comprise a covector field on the configuration manifold. The invariance of the inner product p v under point transformations provides the motivation for our use of superscripts for velocity components and subscripts for momentum components.