 , I
, I
Canonical transformations allow us to change the phase-space coordinate system that we use to express a problem, preserving the form of Hamilton's equations. If we solve Hamilton's equations in one phase-space coordinate system we can use the transformation to carry the solution to the other coordinate system. What other properties are preserved by a canonical transformation?
We noted in equation (5.10) that canonical
extensions of point transformations preserve the value of p v.
This does not hold for more general canonical transformations. We can
illustrate this with the transformation just considered. Along
corresponding paths x, px and  , I
, I

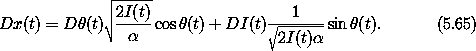
The difference of p v and the transformed p' v' is
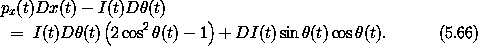
In general this is not zero. The product pv is not necessarily invariant under general canonical transformations.
Here is a remarkable fact: the composition of the Poisson bracket of two phase-space state functions with a canonical transformation is the same as the Poisson bracket of each of the two functions composed with the transformation separately. Loosely speaking, the Poisson bracket is invariant under canonical phase-space transformations.
Let f and g be two phase-space state functions.
Using the 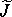 representation of the Poisson bracket (see
section 5.2.4), we deduce
representation of the Poisson bracket (see
section 5.2.4), we deduce
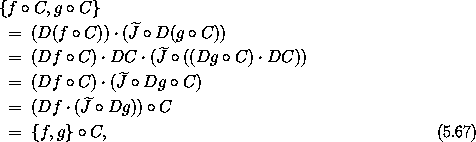
where the fact that C is symplectic and satisfies equation (5.52) was used in the middle. Abstracted to functions of phase-space states, this is

Consider a canonical transformation C. Let 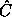 t be a
function with parameter t such that (q, p) =
t be a
function with parameter t such that (q, p) = 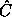 t(q', p') if
(t, q, p) = C(t, q', p'). The function
t(q', p') if
(t, q, p) = C(t, q', p'). The function 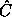 t maps phase-space
coordinates to alternate phase-space coordinates at a given time.
Consider regions R in (q, p) and R' in (q', p') such
that R =
t maps phase-space
coordinates to alternate phase-space coordinates at a given time.
Consider regions R in (q, p) and R' in (q', p') such
that R = 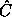 t(R'). The volume of region R' is
t(R'). The volume of region R' is

where 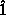 is the function whose value is one for every input.
Now if C is symplectic then the determinant of D
is the function whose value is one for every input.
Now if C is symplectic then the determinant of D 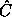 t is one
(see section 4.2), so
t is one
(see section 4.2), so

Thus, phase-space volume is preserved by symplectic transformations.
Liouville's theorem shows that time evolution preserves phase-space volume. Here we see that canonical transformations also preserve phase volumes. Later, we will find that time evolution actually generates a canonical transformation.
The invariance of Poisson brackets under canonical transformations can be used to prove the invariance of another closely related antisymmetric bilinear form under canonical transformations. Define11
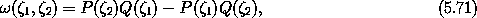
where Q = I1 and P = I2 are the coordinate and momentum selectors,
respectively. The arguments 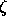 1 and
1 and 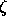 2 are incremental
phase-space states. Under a canonical transformation s = C(s'),
incremental states transform with the derivative
2 are incremental
phase-space states. Under a canonical transformation s = C(s'),
incremental states transform with the derivative


provided the 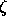 i' have zero time component.
i' have zero time component.
Condition (5.27) that a time-independent C with compositional Hamiltonian H is canonical is equivalent to the symplectic condition (5.31), which does not mention the Hamiltonian H. So for time-independent symplectic C, condition (5.27) is also satisfied with the Hamiltonian replaced by any function f on the phase-state space:
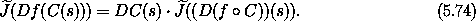
We will use this in the following.
In terms of 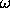 , the Poisson bracket is
, the Poisson bracket is
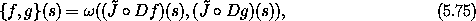
as can be seen by writing out the components. We use the fact that Poisson brackets are invariant under canonical transformations:
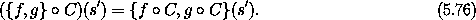
The left-hand side of equation (5.76) is
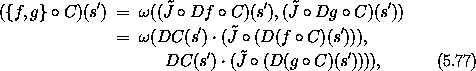
where we have used the relation (5.74). The right-hand side of equation (5.76) is
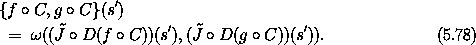
Now the left-hand side must equal the right-hand side for any f
and g, so the equation must also be true for arbitrary 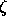 i' of the form
i' of the form

The 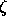 'i are arbitrary incremental states with zero time components.
'i are arbitrary incremental states with zero time components.
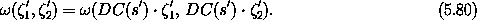
for canonical C and incremental states 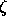 'i with zero time
components. Using equation (5.72), we have
'i with zero time
components. Using equation (5.72), we have

Thus the bilinear antisymmetric function 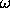 is invariant under
canonical transformations.
is invariant under
canonical transformations.
As a program, 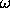 is
is
(define (omega zeta1 zeta2)
(- (* (momentum zeta2) (coordinate zeta1))
(* (momentum zeta1) (coordinate zeta2))))
We can check that it is invariant under the polar to rectangular canonical transformation by computing the residuals. We use the arbitrary state
(define a-polar-state
(up 't
(up 'r 'phi)
(down 'pr 'pphi)))
and the typical state increments
(define zeta1
(up 0
(up 'dr1 'dphi1)
(down 'dpr1 'dpphi1)))
(define zeta2
(up 0
(up 'dr2 'dphi2)
(down 'dpr2 'dpphi2)))
Note that the time components of zeta1 and zeta2 are zero. We evaluate the residual:
(print-expression
(let ((DCs ((D (F->CT p->r)) a-polar-state)))
(- (omega zeta1 zeta2)
(omega (* DCs zeta1) (* DCs zeta2)))))
0
The residual is zero so 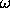 is invariant under this canonical
transformation.
is invariant under this canonical
transformation.
Consider the oriented area of a region R' in phase space (see figure 5.2). Suppose we make a canonical transformation from coordinates (q', p') to (q, p) taking region R' to region R. The boundary of the region in the transformed coordinates is just the image under the canonical transformation of the original boundary. Let Rqi, pi be the projection of the region R onto the qi, pi plane of coordinate qi and conjugate momentum pi, and let Ai be its area. We call the qi, pi plane the ith canonical plane in these phase-space variables. Similarly, let R'q'i, p'i be the projection of R' onto the q'i, p'i plane, and let A'i be its area. Then it turns out that the sums of the areas of the projections of R and of R' are the same:

That is, the sum of the projected areas on the canonical planes is preserved by canonical transformations. Another way to say this is
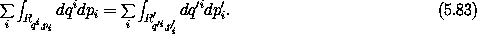
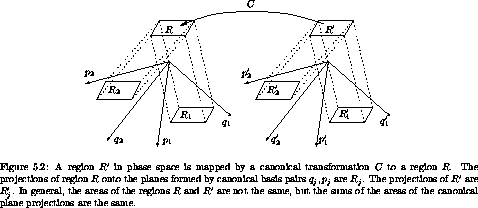
To see why this is true, we first consider how the area of an
incremental parallelogram in phase space transforms under canonical
transformation. Let (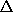 q,
q, 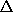 p) and (
p) and (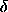 q,
q, 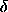 p)
be small increments in phase space, originating at (q, p).
Consider the incremental parallelogram with vertex at (q, p) with
these two phase-space increments as edges. The sum of the areas of
the canonical projections of this incremental parallelogram can be
written
p)
be small increments in phase space, originating at (q, p).
Consider the incremental parallelogram with vertex at (q, p) with
these two phase-space increments as edges. The sum of the areas of
the canonical projections of this incremental parallelogram can be
written

The right-hand side is the sum of the areas on the canonical planes;
for each i the area of a parallelogram is computed from
the components of the vectors defining its adjacent sides. Let
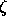 1 = (0 ,
1 = (0 , 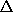 q,
q, 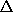 p) and
p) and 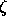 2 = (0 ,
2 = (0 , 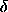 q,
q,
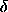 p); then the sum of the areas of the incremental
parallelograms is just
p); then the sum of the areas of the incremental
parallelograms is just

where 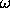 is the bilinear antisymmetric function introduced
in equation (5.71). The function
is the bilinear antisymmetric function introduced
in equation (5.71). The function 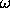 is invariant under canonical
transformations, so the sum of the areas of the incremental
parallelograms is invariant under canonical transformations.
is invariant under canonical
transformations, so the sum of the areas of the incremental
parallelograms is invariant under canonical transformations.
The area of an arbitrary region is just the limit of the sum of the areas of incremental parallelograms that cover the region, so the sum of oriented areas is preserved by canonical transformations:

We define an action-like region to be one for which canonical coordinates can be chosen so that the region is entirely in the subspace spanned by a particular canonical pair qi, pi. For this coordinate system the projection on that plane has all of the area. The projections on the other canonical planes have no area. So the sum of the areas of the canonical projections is just the area of the region itself. The sum of the areas of the projections onto canonical planes is preserved under canonical transformation, so the area of an action-like region is the sum of the areas of the canonical projections for any canonical coordinate system.
There are also regions that have no action-like projection. For example, a region in the plane qi, qj has no action-like projection. Therefore the sum of the areas of the canonical projections is zero, and this is the case for any canonical coordinate system, though in other canonical coordinates some of the projections may have nonzero area to be balanced by negative area of others.
The equality-of-areas relation (5.83) can also be written as an equality of line integrals using Stokes's theorem, for simply-connected regions Rqi, pi and R'q'i, p'i:
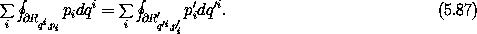
The canonical planes are disjoint except at the origin, so the projected areas intersect in at most one point. Thus we may independently accumulate the line integrals around the boundaries of the individual projections of the region onto the canonical planes into a line integral around the unprojected region:

Consider the canonical transformation C:
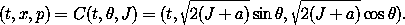
a. Show that the transformation is symplectic for any a.
b. Show that equation (5.88) is not generally satisfied for the region enclosed by a curve of constant J.
11 The 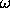 form can also be written as a sum over
degrees of freedom:
form can also be written as a sum over
degrees of freedom:
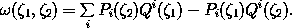
Notice that the contributions for each i do not mix components from different degrees of freedom.
This bilinear form is closely related to the symplectic 2-form of differential geometry. It differs in that the symplectic 2-form is formally a function of the phase-space point as well as the incremental vectors.