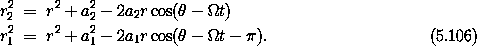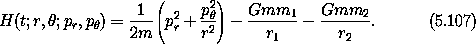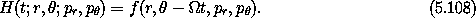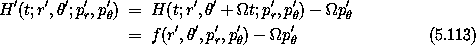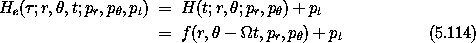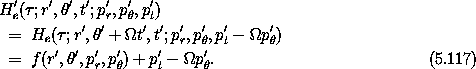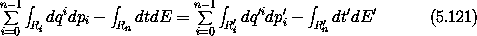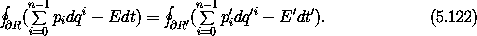In this section we show that we can treat time as just another
coordinate if we wish. Systems described by a time-dependent
Hamiltonian may be recast in terms of a time-independent Hamiltonian
with an extra degree of freedom. An advantage of this view is that
what was a time-dependent canonical transformation can be treated as a
time-independent transformation, where there are no additional
conditions for adjusting the Hamiltonian.
Suppose that we have some system characterized by a time-dependent
Hamiltonian, for example, a periodically driven pendulum. We may
imagine that there is some extremely massive oscillator, unperturbed
by the motion of the relatively massless pendulum, that produces the
drive. Indeed, we may think of time itself as the coordinate of an
infinitely massive particle moving uniformly and driving everything
else. We often consider the rotation of the Earth as exactly such a
stable time reference when performing short-time experiments in the
laboratory.
More formally, consider a dynamical system with n degrees of
freedom, whose behavior is described by a possibly time-dependent
Lagrangian L with corresponding Hamiltonian H. We make a new
dynamical system with n + 1 degrees of freedom by extending the
generalized coordinates to include time and introducing a new
independent variable. We also extend the generalized velocities to
include a velocity for the time coordinate. In this new extended
state space the coordinates are redundant, so there is a constraint
relating the time coordinate to the new independent variable.
We relate the original dynamical system to the extended dynamical
system as follows: Let q be a coordinate path.
Let qe,t : 
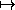 qe(
qe( ),t(
),t( )
be a coordinate path in the extended system where
)
be a coordinate path in the extended system where  is the new
independent variable. Then qe = q o t, or qe(
is the new
independent variable. Then qe = q o t, or qe( ) =
q(t(
) =
q(t( )). Consequently, if v = Dq is the velocity along a
path then ve(
)). Consequently, if v = Dq is the velocity along a
path then ve( ) = D qe(
) = D qe( ) = Dq(t(
) = Dq(t( )) · Dt(
)) · Dt( ) = v(t(
) = v(t( )) ·
vt(
)) ·
vt( ).
).
We can find a Lagrangian for the extended system by requiring
that the value of the action be unchanged.
Introduce the extended Lagrangian action
with
We have
The extended system is subject to a constraint that relates the time
to the new independent variable. We assume the constraint is of the
form  (
( ; qe, qt; ve, vt) = qt - f(
; qe, qt; ve, vt) = qt - f( ) = 0. The
constraint is a holonomic constraint
involving the coordinates and time, so we can incorporate this
constraint by augmenting the Lagrangian:12
) = 0. The
constraint is a holonomic constraint
involving the coordinates and time, so we can incorporate this
constraint by augmenting the Lagrangian:12
The Lagrange equations of L'e for qe are satisfied for the paths
q o t where q is any path that satisfies the original Lagrange
equations of L.
The momenta conjugate to the coordinates are
So the extended momenta have the same values as the original momenta
at the corresponding states. The momentum conjugate to the time
coordinate is the negation of the energy plus v . The
momentum conjugate to
. The
momentum conjugate to  is the constraint, which must be zero.
is the constraint, which must be zero.
Next we carry out the transformation to the corresponding Hamiltonian
formulation. First, note that the Lagrangian Le is a homogeneous
form of degree one in the velocities. Thus, by Euler's theorem,
The p -part of the Legendre transform of Le' is
-part of the Legendre transform of Le' is
So the Hamiltonian H'e corresponding to L'e is
We have used the fact that that at corresponding states the momenta
have the same values, so on paths pe = p o t, and
The Hamiltonian H'e does not depend on  so we deduce that
p
so we deduce that
p is constant. In fact, p
is constant. In fact, p must be given the value
zero, because it is the constraint. When there is a cyclic coordinate
we can form a reduced Hamiltonian for the remaining degrees of freedom
by substituting the constant value of conserved momentum conjugate to
the cyclic coordinate into the Hamiltonian. The resulting Hamiltonian
is
must be given the value
zero, because it is the constraint. When there is a cyclic coordinate
we can form a reduced Hamiltonian for the remaining degrees of freedom
by substituting the constant value of conserved momentum conjugate to
the cyclic coordinate into the Hamiltonian. The resulting Hamiltonian
is
This extended Hamiltonian governs the evolution of the extended
system, for arbitrary f.13
Hamilton's equations reduce to
The second equation gives the required relation between t and  .
The first and third equations are equivalent to Hamilton's equations
in the original coordinates, as we can see by
using qe = q o t to rewrite them:
.
The first and third equations are equivalent to Hamilton's equations
in the original coordinates, as we can see by
using qe = q o t to rewrite them:
Using Dt( ) = Df(
) = Df( ) and dividing these factors out, we
recover Hamilton's equations.14
) and dividing these factors out, we
recover Hamilton's equations.14
Now consider the special case for which the time is the same as the
independent variable: f( ) =
) =  , Df(
, Df( ) = 1. In this
case q = qe and p = pe. The extended Hamiltonian becomes
) = 1. In this
case q = qe and p = pe. The extended Hamiltonian becomes
Hamilton's equation for t becomes Dt( ) = 1, restating the
constraint.
The Hamilton's equations for Dqe and Dpe are directly Hamilton's
equations:
) = 1, restating the
constraint.
The Hamilton's equations for Dqe and Dpe are directly Hamilton's
equations:
The extended Hamiltonian (5.103) does
not depend on the independent variable, so it is a conserved quantity.
Thus, up to an additive constant pt is equal to minus the energy. The
Hamilton's equation for Dpt relates the change of the energy to
 0 H. Note that in the more general case, the momentum
conjugate to the time is not the negation of the energy. This choice,
t(
0 H. Note that in the more general case, the momentum
conjugate to the time is not the negation of the energy. This choice,
t( ) =
) =  , is useful for a number of applications.
, is useful for a number of applications.
Note that the extension transformation is canonical in the sense that
the two sets of equations of motion describe equivalent dynamics.
However, the transformation is not symplectic; in fact, it does not
even have the same number of input and output variables.
Exercise 5.10. Homogeneous extended Lagrangian
Verify that Le is homogeneous of degree one in the velocities.
Exercise 5.11. Lagrange equations
a. Verify the claim that
the Lagrange equations for qe are satisfied for exactly the same
trajectories that satisfy the original Lagrange equations for q.
b. Verify the claim that the Lagrange equation for t relates
the rate of change of energy to  0 L.
0 L.
Exercise 5.12. Lorentz transformations
Investigate Lorentz transformations as point transformations in the
extended phase space.
An example that shows the utility of reformulating a problem in the
extended phase space is the restricted three-body problem: the motion
of a low-mass particle subject to the gravitational attraction of two
other massive bodies that move in some fixed orbit. The problem is
an idealization of the situation where a body with very small mass
moves in the presence of two bodies with much larger masses. Any
effects of the smaller body on the larger bodies are neglected. In the
simplest version, the motion of all three bodies is assumed to be in
the same plane, and the orbit of the two massive bodies is circular.
The motion of the bodies with larger masses is not influenced
by the small mass, so we model this situation as the small body moving in
a time-varying field of the larger bodies undergoing a prescribed
motion. This situation can be captured as a time-dependent
Hamiltonian:
where r1 and r2 are the distances of the small body to the
larger bodies, m is the mass of the small body, and m1
and m2 are the masses of the larger bodies. Note that r1 and
r2 are quantities that depend both on the position of the small
particle and the time varying position of the massive particles.
The massive bodies are in circular orbits and maintain constant
distance from the center of mass. Let a1 and a2 be the
distances to the center of mass; then the distances satisfy m1 a1 = m2
a2. The angular frequency is 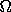 = (G(m1 + m2)/a3)1/2
where a is the distance between the masses.
= (G(m1 + m2)/a3)1/2
where a is the distance between the masses.
In polar coordinates, with the center of mass of the subsystem of
massive particles at the origin and with r and  describing
the position of the low-mass particle, the positions of the two massive
bodies are a2 = m1 a / (m1 + m2) with
describing
the position of the low-mass particle, the positions of the two massive
bodies are a2 = m1 a / (m1 + m2) with  2 =
2 = 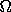 t ,
a1 = m2 a / (m1 + m2) with
t ,
a1 = m2 a / (m1 + m2) with  1 =
1 = 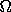 t +
t +  . The
distances to the point masses are
. The
distances to the point masses are
So, in polar coordinates, the Hamiltonian is
We see therefore that the Hamiltonian can be written in
terms of some function f such that
The essential feature is that  and t appear in the Hamiltonian
only in the combination
and t appear in the Hamiltonian
only in the combination  -
- 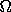 t.
t.
One way to get rid of the time dependence is to choose a new set of
variables with one coordinate equal to this combination  -
-
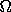 t, by making a point transformation to a rotating coordinate
system. We have shown that
t, by making a point transformation to a rotating coordinate
system. We have shown that
with
is a canonical transformation. The new Hamiltonian, which is not the
energy, is conserved because there is no explicit time dependence. It
is a useful integral of motion -- the Jacobi constant.15
We can also eliminate the dependence on the independent time-like
variable from the Hamiltonian for the restricted problem by going to
the extended phase space, choosing t =  . The Hamiltonian
. The Hamiltonian
is autonomous and is consequently an integral of the motion.
Again, we see that  and t occur only in the combination
and t occur only in the combination
 -
- 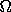 t,
which suggests a point transformation to a new coordinate
t,
which suggests a point transformation to a new coordinate  '
=
'
=  -
- 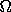 t. This point transformation is independent of the
new independent variable
t. This point transformation is independent of the
new independent variable  .
The transformation is specified in equations (5.109-5.112),
augmented by relations specifying how the time coordinate and its
conjugate momentum are handled:
.
The transformation is specified in equations (5.109-5.112),
augmented by relations specifying how the time coordinate and its
conjugate momentum are handled:
The new Hamiltonian is obtained by composing the old Hamiltonian
with the transformation:
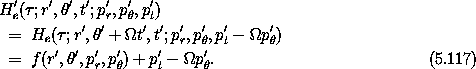
We recognize that the new Hamiltonian in the extended phase space,
which has the same value as the original Hamiltonian in the extended
phase space, is just the Jacobi constant plus p't. The new
Hamiltonian does not depend on t', so p't is a constant of the
motion. In fact, its value is irrelevant to the rest of the dynamical
evolution, so we may set the value of p't to zero if we like. Thus,
we have found that the Hamiltonian in the extended phase space, which
is conserved, is just the Jacobi constant plus an additive arbitrary
constant. We have two routes to the Jacobi constant: (1) transform
the original system to a rotating coordinate system to eliminate the time
dependence, but in the process add extra terms to the Hamiltonian, and (2) go
to the extended phase space and immediately get an integral, and by
going to rotating coordinates recognize that this Hamiltonian
is the same as the Jacobi constant. So sometimes the Hamiltonian in
the extended phase space is a useful integral.
Exercise 5.13. Transformations in the extended phase space
In section 5.2.3 we found that
time-dependent transformations for which the derivative of the
coordinate-momentum part is symplectic are canonical only if the
Hamiltonian is modified by adding a function K subject to certain
constraints (equation 5.54). Show that the
constraints on K follow from the symplectic condition in the
extended phase space, using the choice t =  .
.
A time-dependent transformation is canonical if in the extended phase
space the Hamiltonians transform by composition and the extended
phase-space transformation is symplectic.
In section 5.3
we showed that if the derivative of the
transformation is symplectic then the sum of the areas of the
projections of any two-dimensional region of phase space onto the
canonical qi, pi planes is preserved.
This invariance is also true of symplectic transformations in the extended phase space.
Let R and R' be corresponding regions of extended phase-space
coordinates. Let Ai be the area of the projection of the region R onto the
canonical qi, pi plane, and A'i be the area of the projection
of the corresponding region R' onto the
canonical q'i, p'i plane.
In the extended phase space, we also have a projection onto the t, pt
canonical plane. Let An be the area of the projection onto
the t, pt plane. We have then
In terms of integrals this is
This equality for the sum of area integrals can be rewritten in terms
of line integrals by Stokes's theorem:
where the order of the integration and summation can be reversed
because the boundary of R projects to the boundary on the canonical
planes.
For the special choice of t =  this result can be rephrased in an
interesting way. Let E be the
value of the Hamiltonian in the original unextended phase space.
Using qn = t and pn = pt = - E, we can write
this result can be rephrased in an
interesting way. Let E be the
value of the Hamiltonian in the original unextended phase space.
Using qn = t and pn = pt = - E, we can write
and
The relations (5.121) and
(5.122) are two
formulations of the Poincaré-Cartan integral invariant.

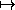 qe(
qe( ),t(
),t( )
be a coordinate path in the extended system where
)
be a coordinate path in the extended system where  is the new
independent variable. Then qe = q o t, or qe(
is the new
independent variable. Then qe = q o t, or qe( ) =
q(t(
) =
q(t( )). Consequently, if v = Dq is the velocity along a
path then ve(
)). Consequently, if v = Dq is the velocity along a
path then ve( ) = D qe(
) = D qe( ) = Dq(t(
) = Dq(t( )) · Dt(
)) · Dt( ) = v(t(
) = v(t( )) ·
vt(
)) ·
vt( ).
).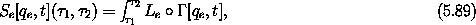
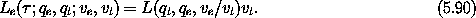
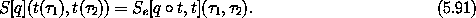
 (
(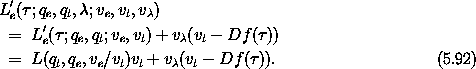
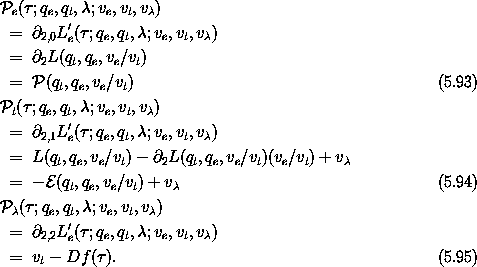
 . The
momentum conjugate to
. The
momentum conjugate to 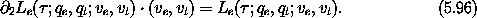
 -part of the Legendre transform of Le' is
-part of the Legendre transform of Le' is
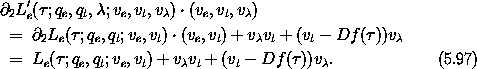
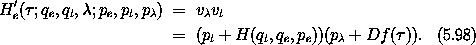

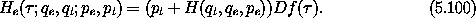
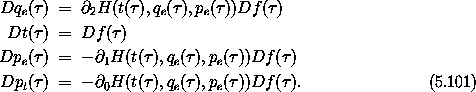
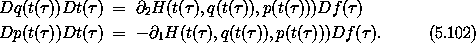
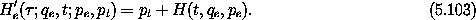
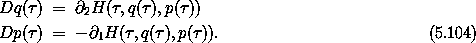
 0 H. Note that in the more general case, the momentum
conjugate to the time is not the negation of the energy. This choice,
t(
0 H. Note that in the more general case, the momentum
conjugate to the time is not the negation of the energy. This choice,
t(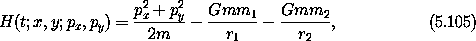
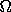 = (G(m1 + m2)/a3)1/2
where a is the distance between the masses.
= (G(m1 + m2)/a3)1/2
where a is the distance between the masses. describing
the position of the low-mass particle, the positions of the two massive
bodies are a2 = m1 a / (m1 + m2) with
describing
the position of the low-mass particle, the positions of the two massive
bodies are a2 = m1 a / (m1 + m2) with  . The
distances to the point masses are
. The
distances to the point masses are