
Suppose we have a system with n + 1 degrees of freedom described by a time-independent Hamiltonian in a (2n + 2)-dimensional phase space. Here we can play the converse game: we can choose any generalized coordinate to play the role of ``time'' and the negation of its conjugate momentum to play the role of a new n-degree-of-freedom time-dependent Hamiltonian in a reduced phase space of 2n dimensions.

and suppose we have a system described by a time-independent Hamiltonian

For each solution path there is a conserved quantity E. Let's choose a coordinate qn to be the time in a reduced phase space. We define the dynamical variables for the n-degree-of-freedom reduced phase space:

In the original phase space a coordinate such as qn maps time to a
coordinate. In the formulation of the reduced phase space we will
have to use the inverse function  = (qn)-1 to map the coordinate to
the time, giving the new coordinates in terms of the new time
= (qn)-1 to map the coordinate to
the time, giving the new coordinates in terms of the new time

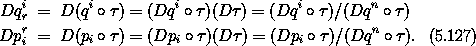
We propose that a Hamiltonian in the reduced phase space is the negative of the inverse of f(q0, ..., qn; p0, ..., pn) = E with respect to the pn argument:
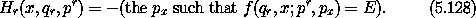
Note that in the reduced phase space we will have indices for the structured variables in the range 0 ... n - 1, whereas in the original phase space the indices are in the range 0 ... n. We will show that Hr is an appropriate Hamiltonian for the given dynamical system in the reduced phase space. To compute Hamilton's equations we must expand the implicit definition of Hr. We define an auxiliary function
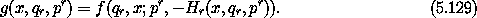
Note that by construction this function is identically a constant g = E. Thus all of its partial derivatives are zero:
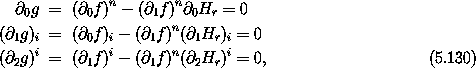
where we have suppressed the arguments. Solving for partials of Hr, we get
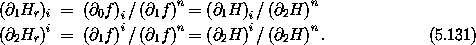
Using these relations, we can deduce the Hamilton's equations in the reduced phase space from the Hamilton's equations in the original phase space:
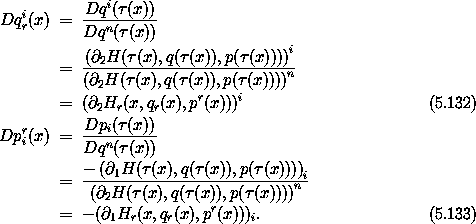
Consider planar motion in a central field. We have already seen this expressed in polar coordinates in equation (3.99):
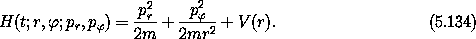
There are two degrees of freedom and the Hamiltonian is time independent. Thus the energy, the value of the Hamiltonian, is conserved on realizable paths. Let's forget about time and reparameterize this system in terms of the orbital radius r.16 To do this we solve

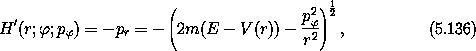
which is the Hamiltonian in the reduced phase space.
Hamilton's equations are now quite simple:
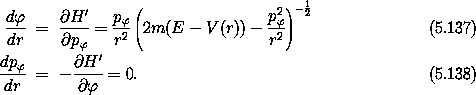
We see that p is independent of r (as it was with t), so for
any particular orbit we may define a constant angular momentum L.
Thus our problem ends up as a simple quadrature:
is independent of r (as it was with t), so for
any particular orbit we may define a constant angular momentum L.
Thus our problem ends up as a simple quadrature:
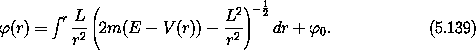
To see the utility of this procedure, we continue our example with a definite potential energy -- a gravitating mass point:

When we substitute this into equation (5.139) we obtain a mess that can be simplified to
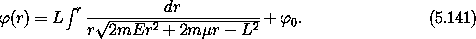
Integrating this, we obtain another mess, which can be simplified and rearranged to obtain the following:
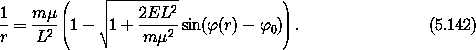
This can be recognized as the polar-coordinate form of the equation of a conic section with eccentricity e and parameter p:

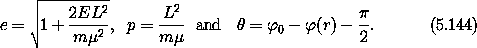
In fact, if the orbit is an ellipse with semimajor axis a, we have

and so we can identify the role of energy and angular momentum in shaping the ellipse:
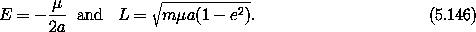
What we get from analysis in the reduced phase space is the geometry of the trajectory, but we lose the time-domain behavior. The reduction is often worth the price.
Although we have treated time in a special way so far, we have found that time is not special. It can be included in the coordinates to make a driven system autonomous. And it can be eliminated from any autonomous system in favor of any other coordinate. This leads to numerous strategies for simplifying problems, by removing time variation and then performing canonical transforms on the resulting conservative autonomous system to make a nice coordinate that we can then dump back into the role of time.
16 We
could have chosen to reparameterize in terms of  , but then both
pr and r would occur in the resulting time-independent
Hamiltonian. The path we have chosen takes advantage of the fact that
, but then both
pr and r would occur in the resulting time-independent
Hamiltonian. The path we have chosen takes advantage of the fact that
 does not appear in our Hamiltonian, so p
does not appear in our Hamiltonian, so p is a constant
of the motion. This structure suggests that to solve this kind of
problem we need to look ahead, as in playing chess.
is a constant
of the motion. This structure suggests that to solve this kind of
problem we need to look ahead, as in playing chess.