Our motivation for the development of Hamilton's equations was to
focus attention on the quantities that can be conserved -- the
momenta and the energy. In the Hamiltonian formulation the
generalized configuration coordinates and the conjugate momenta
comprise the state of the system at a given time.
We know from the
Lagrangian formulation that if the Lagrangian does not depend on some
coordinate then the conjugate momentum is conserved. This is also
true in the Hamiltonian formulation, but there is a distinct advantage
to the Hamiltonian formulation. In the Lagrangian formulation the
knowledge of the conserved momentum does not lead immediately to any
simplification of the problem, but in the Hamiltonian formulation the
fact that momenta are conserved gives an immediate reduction in the
dimension of the system to be solved.
In fact, if a coordinate does not appear in the Hamiltonian then the
dimension of the system of coupled equations that remain to be solved
is reduced by two -- the coordinate does not appear and the conjugate
momentum is constant.
Let H(t, q, p) be a Hamiltonian for some
problem with an n-dimensional configuration space and
2n-dimensional phase space. Suppose the Hamiltonian does not
depend upon the ith coordinate qi: ( 1 H)i = 0.19
According to Hamilton's equations, the conjugate momentum pi is
conserved. Hamilton's equations of motion for the remaining 2n - 2
phase-space variables do not involve qi (because it does not appear
in the Hamiltonian), and pi is a constant. Thus the dimension of
the difficult part of the problem, the part that involves the solution
of coupled ordinary differential equations, is reduced by two. The
remaining equation governing the evolution of qi in general depends
on all the other variables, but once the reduced problem has been
solved, the equation of motion for qi can be written so as to
give Dqi explicitly as a function of time. We can then find
qi as a definite integral of this function.20
1 H)i = 0.19
According to Hamilton's equations, the conjugate momentum pi is
conserved. Hamilton's equations of motion for the remaining 2n - 2
phase-space variables do not involve qi (because it does not appear
in the Hamiltonian), and pi is a constant. Thus the dimension of
the difficult part of the problem, the part that involves the solution
of coupled ordinary differential equations, is reduced by two. The
remaining equation governing the evolution of qi in general depends
on all the other variables, but once the reduced problem has been
solved, the equation of motion for qi can be written so as to
give Dqi explicitly as a function of time. We can then find
qi as a definite integral of this function.20
Contrast this result with analogous results for more general systems
of differential equations. There are two independent situations.
One situation is that we know a constant of the motion. In general,
constants of the motion can be used to reduce by one the dimension of the
unsolved part of the problem. To see this, let the system of
equations be
where m is the dimension of the system. Assume we know some
constant of the motion
At least locally, we expect that we can use this equation to solve for
zm-1(t) in terms of all the other variables, and use this solution to
eliminate the dependence on zm-1(t). The first m - 1 equations then
depend only upon the first m - 1 variables. The dimension of the
system of equations to be solved is reduced by one. After the
solution for the other variables has been found, zm-1(t) can be found
using the constant of the motion.
The second situation is that one of the variables, say zi, does not
appear in the equations of motion (but there is an equation
for Dzi).
In this case the equations for the other variables form an
independent set of equations of one dimension less than the original
system. After these are solved, then the remaining equation for zi
can be solved by definite integration.
In both situations the dimension of the system of coupled equations is
reduced by one. Hamilton's equations are different in that
these two situations often come together. If a Hamiltonian for a
system does not depend on a particular coordinate, then the equations of
motion for the other coordinates and momenta do not depend on that
coordinate. Furthermore, the momentum conjugate to that coordinate is
a constant of the motion. An added benefit is that the use of this
constant of the motion to reduce the dimension of the remaining
equations is automatic in the Hamiltonian formulation. The conserved
momentum is a state variable and just a parameter in the
remaining equations.
So if there is a continuous symmetry it will probably be to our
advantage to choose a coordinate system that explicitly
incorporates the symmetry, making the Hamiltonian independent of a
coordinate. Then the dimension of the phase space of the coupled
system will be reduced by two for every coordinate that does not
appear in the Hamiltonian.21
Consider the motion of a particle of mass m in a central potential. A
natural choice for generalized coordinates that reflects the symmetry is polar
coordinates. A Lagrangian is (equation 1.67):
The momenta are pr = m 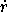 and p
and p = m r2
= m r2 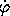 .
The kinetic energy is a homogeneous quadratic form in the velocities,
so the Hamiltonian is T + V with the velocities rewritten in
terms of the momenta:
.
The kinetic energy is a homogeneous quadratic form in the velocities,
so the Hamiltonian is T + V with the velocities rewritten in
terms of the momenta:
Hamilton's equations are
The potential energy depends on the distance from the origin, r, as does
the kinetic energy in polar coordinates, but neither the potential
energy nor
the kinetic energy depends on the polar angle  . The angle
. The angle
 does not appear in the Lagrangian so we know that
p
does not appear in the Lagrangian so we know that
p , the momentum conjugate to
, the momentum conjugate to  , is conserved along
realizable trajectories. The fact that p
, is conserved along
realizable trajectories. The fact that p is constant along
realizable paths is expressed by one of Hamilton's equations. That
p
is constant along
realizable paths is expressed by one of Hamilton's equations. That
p has a constant value is immediately made use of in the
other Hamilton's equations: the remaining equations are a
self-contained subsystem with constant p
has a constant value is immediately made use of in the
other Hamilton's equations: the remaining equations are a
self-contained subsystem with constant p . To make a
lower-dimensional subsystem in the Lagrangian formulation we have to use each
conserved momentum to eliminate one of the other state variables, as we
did for the axisymmetric top (see section 2.10).
. To make a
lower-dimensional subsystem in the Lagrangian formulation we have to use each
conserved momentum to eliminate one of the other state variables, as we
did for the axisymmetric top (see section 2.10).
We can check our derivations with the computer.
A procedure implementing the Lagrangian has already been introduced
(below equation 1.67). We can use this
to get the Hamiltonian:
(show-expression
((Lagrangian->Hamiltonian
(L-central-polar 'm (literal-function 'V)))
(up 't (up 'r 'phi) (down 'p_r 'p_phi))))
and to develop Hamilton's equations:
(show-expression
(((Hamilton-equations
(Lagrangian->Hamiltonian
(L-central-polar 'm (literal-function 'V))))
(up (literal-function 'r)
(literal-function 'phi))
(down (literal-function 'p_r)
(literal-function 'p_phi)))
't))
We reconsider the axisymmetric top (see
section 2.10) from the Hamiltonian point of
view. Recall that a top is a rotating rigid body, one point of which
is fixed in space. The center of mass is not at the fixed point, and
there is a uniform gravitational field. An axisymmetric top is a top
with an axis of symmetry. We consider here an axisymmetric top with
the fixed point on the symmetry axis.
The axisymmetric top has two continuous symmetries we would like
to exploit. It has the symmetry that neither the kinetic nor
potential energy is sensitive to the orientation of the top about the
symmetry axis. The kinetic and potential energy are also insensitive
to a rotation of the physical system about the vertical axis, because
the gravitational field is uniform. We take advantage of these
symmetries by choosing coordinates that naturally express them. We
already have an appropriate coordinate system that does the job -- the
Euler angles. We choose the reference orientation of the top so that
the symmetry axis is vertical. The first Euler angle  expresses
a rotation about the symmetry axis. The next Euler angle
expresses
a rotation about the symmetry axis. The next Euler angle  is
the tilt of the symmetry axis of the top from the vertical. The third
Euler angle
is
the tilt of the symmetry axis of the top from the vertical. The third
Euler angle  expresses a rotation of the top about the fixed
z axis. The symmetries of the problem imply that the first and
third Euler angles do not appear in the Hamiltonian. As a consequence
the momenta conjugate to these angles are conserved quantities. The
problem of determining the motion of the axisymmetric top is reduced
to the problem of determining the evolution of
expresses a rotation of the top about the fixed
z axis. The symmetries of the problem imply that the first and
third Euler angles do not appear in the Hamiltonian. As a consequence
the momenta conjugate to these angles are conserved quantities. The
problem of determining the motion of the axisymmetric top is reduced
to the problem of determining the evolution of  and
p
and
p . Let's work out the details.
. Let's work out the details.
In terms of Euler angles, a Lagrangian for the axisymmetric top is
(see section 2.10):
(define ((L-axisymmetric-top A C gMR) local)
(let ((q (coordinate local))
(qdot (velocity local)))
(let ((theta (ref q 0))
(thetadot (ref qdot 0))
(phidot (ref qdot 1))
(psidot (ref qdot 2)))
(+ (* 1/2 A
(+ (square thetadot)
(square (* phidot (sin theta)))))
(* 1/2 C
(square (+ psidot (* phidot (cos theta)))))
(* -1 gMR (cos theta))))))
where gMR is the product of the gravitational
acceleration, the mass of the top, and the distance from
the point of support to the center of mass. The Hamiltonian is nicer
than we have a right to expect:
(show-expression
((Lagrangian->Hamiltonian (L-axisymmetric-top 'A 'C 'gMR))
(up 't
(up 'theta 'phi 'psi)
(down 'p_theta 'p_phi 'p_psi))))
Note that the angles  and
and  do not appear in the
Hamiltonian, as expected. Thus the momenta p
do not appear in the
Hamiltonian, as expected. Thus the momenta p and p
and p are
constants of the motion.
are
constants of the motion.
For given values of p and p
and p we must determine the
evolution of
we must determine the
evolution of  and p
and p . The effective Hamiltonian for
. The effective Hamiltonian for  and p
and p has one degree of freedom,
and does not involve the time. Thus the value of the
Hamiltonian is conserved along realizable trajectories. So
the trajectories of
has one degree of freedom,
and does not involve the time. Thus the value of the
Hamiltonian is conserved along realizable trajectories. So
the trajectories of  and p
and p trace
contours of the effective Hamiltonian. This gives us a big
picture of the possible types of motion and their relationship, for
given values of p
trace
contours of the effective Hamiltonian. This gives us a big
picture of the possible types of motion and their relationship, for
given values of p and p
and p .
.
If the top is standing vertically then p = p
= p . Let's
concentrate on the case that p
. Let's
concentrate on the case that p = p
= p , and define p =
p
, and define p =
p = p
= p . The effective Hamiltonian becomes (after a little
trigonometric simplification)
. The effective Hamiltonian becomes (after a little
trigonometric simplification)
Defining the effective potential energy
which parametrically depends on p, the effective
Hamiltonian is
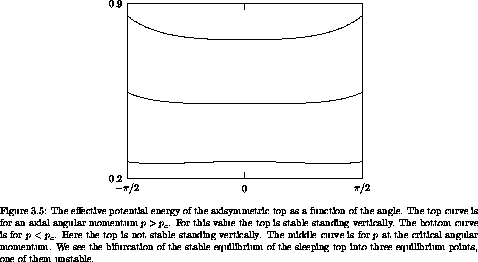
If p is large, Up has a single minimum at  = 0, as
seen in figure 3.5. For small p there is a
minimum for finite positive
= 0, as
seen in figure 3.5. For small p there is a
minimum for finite positive  and a symmetrical minimum for
negative
and a symmetrical minimum for
negative  ; there is a local maximum at
; there is a local maximum at  = 0. There is a
critical value of p at which
= 0. There is a
critical value of p at which  = 0 changes from a minimum
to a local maximum. Denote the critical value by pc. A simple
calculation shows pc = (4 g M R A)1/2. For
= 0 changes from a minimum
to a local maximum. Denote the critical value by pc. A simple
calculation shows pc = (4 g M R A)1/2. For  = 0 we have
p = C
= 0 we have
p = C , where
, where  is the rotation rate. Thus to pc
there corresponds a critical rotation rate
is the rotation rate. Thus to pc
there corresponds a critical rotation rate
For  >
>
 c the top can stand vertically; for
c the top can stand vertically; for  <
<  c the
top falls if slightly displaced from the vertical. The top that
stands vertically is called the ``sleeping'' top.
For a more realistic top, friction gradually slows
the rotation; the rotation rate eventually falls below
the critical rotation rate and the top ``wakes up.''
c the
top falls if slightly displaced from the vertical. The top that
stands vertically is called the ``sleeping'' top.
For a more realistic top, friction gradually slows
the rotation; the rotation rate eventually falls below
the critical rotation rate and the top ``wakes up.''
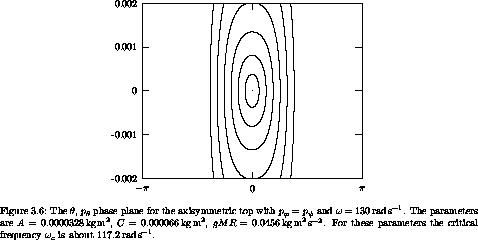

We get additional insight into the sleeping top and the awake top by
looking at the trajectories in the  , p
, p phase plane.
The trajectories in this plane are simply contours of the Hamiltonian,
because the Hamiltonian is conserved. Figure 3.6 shows
a phase portrait for
phase plane.
The trajectories in this plane are simply contours of the Hamiltonian,
because the Hamiltonian is conserved. Figure 3.6 shows
a phase portrait for  >
>  c. All of the trajectories are
loops around the vertical (
c. All of the trajectories are
loops around the vertical ( = 0). Displacing the top slightly
from the vertical simply places the top on a nearby loop, so the top
stays nearly vertical. Figure 3.7 shows the phase
portrait for
= 0). Displacing the top slightly
from the vertical simply places the top on a nearby loop, so the top
stays nearly vertical. Figure 3.7 shows the phase
portrait for  <
<  c. Here the vertical position is an
unstable equilibrium. The trajectories that approach the vertical
are asymptotic -- they take an infinite amount of time to reach it,
just as a pendulum with just the right initial conditions can approach
the vertical but never reach it. If the top is displaced slightly
from the vertical then the trajectories loop around another center
with nonzero
c. Here the vertical position is an
unstable equilibrium. The trajectories that approach the vertical
are asymptotic -- they take an infinite amount of time to reach it,
just as a pendulum with just the right initial conditions can approach
the vertical but never reach it. If the top is displaced slightly
from the vertical then the trajectories loop around another center
with nonzero  . A top started at the center point of the loop
stays there, and one started near this equilibrium point loops stably
around it. Thus we see that when the top ``wakes up'' the vertical is
unstable, but the top does not fall to the ground. Rather, it
oscillates around a new equilibrium.
. A top started at the center point of the loop
stays there, and one started near this equilibrium point loops stably
around it. Thus we see that when the top ``wakes up'' the vertical is
unstable, but the top does not fall to the ground. Rather, it
oscillates around a new equilibrium.
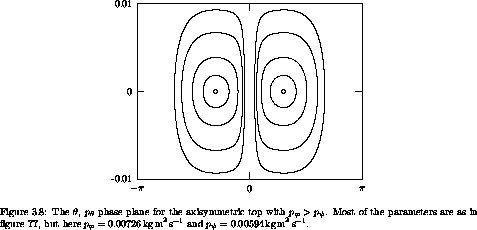
It is also interesting to consider the axisymmetric top when p ne p
ne p . Consider the case p
. Consider the case p > p
> p . Some
trajectories in the
. Some
trajectories in the  , p
, p plane are shown in
figure 3.8. Note that in this case trajectories
do not go through
plane are shown in
figure 3.8. Note that in this case trajectories
do not go through  = 0. The phase portrait for p
= 0. The phase portrait for p <
p
<
p is similar and is not shown.
is similar and is not shown.
We have reduced the motion of the axisymmetric top to quadratures by
choosing coordinates that express the symmetries. It turns out that
the resulting integrals can be expressed in terms of elliptic
functions. Thus, the axisymmetric top can be solved analytically. We
do not dwell on this solution because it is not very illuminating:
since most problems cannot be solved analytically, there is
little profit in dwelling on the analytic solution of one of the rare
problems that is analytically solvable. Rather, we have
focused on the geometry of the solutions in the phase space and the
use of integrals to reduce the dimension of the problem. With the
phase-space portrait we have found some interesting qualitative
features of the motion of the top.
Exercise 3.8. Sleeping top
Verify that the critical angular velocity above which an
axisymmetric top can sleep is given by
equation (3.104).
Suppose there are cyclic coordinates. In the Hamiltonian formulation,
the equations of motion for the coordinates and momenta for the other
degrees of freedom form a self-contained subsystem in which the
momenta conjugate to the cyclic coordinates are parameters. We can
form a Lagrangian for this subsystem by performing a Legendre
transform of the reduced Hamiltonian. Alternatively, we can start
with the full Lagrangian and perform a Legendre transform for only
those coordinates that are cyclic. The equations of motion are
Hamilton's equations for those variables that are transformed and
Lagrange's equations for the others. The momenta conjugate to the
cyclic coordinates are conserved and can be treated as parameters in
the Lagrangian for the remaining coordinates.
Divide the tuple q of coordinates into two subtuples q = (x, y).
Assume L(t; x, y; vx, vy) is a Lagrangian for the system.
Define the Routhian R as the Legendre transform of L with respect
to the vy slot:
To define the function R we must solve
equation (3.105) for vy in terms of the
other variables, and substitute this into
equation (3.105).
Define the state path  :
:
where
Realizable paths satisfy the equations of motion
which are Lagrange's equations for x and Hamilton's
equations for y and py.
Now suppose that the Lagrangian is cyclic in y. Then
 1,1 L =
1,1 L =  1,1 R = 0, and py(t) is a constant
c on any realizable path. Equation (3.113) does not
depend on y, by assumption, and we can replace py by its constant
value c. So equation (3.113) forms a closed
subsystem for the path x. The Lagrangian Lc
1,1 R = 0, and py(t) is a constant
c on any realizable path. Equation (3.113) does not
depend on y, by assumption, and we can replace py by its constant
value c. So equation (3.113) forms a closed
subsystem for the path x. The Lagrangian Lc
describes the motion of the subsystem (the minus sign is introduced
for convenience, and ¤ indicates that the function's value is
independent of this argument).
The path y can be found by integrating
equation (3.114) using the independently determined path
x.
Define the action
The realizable paths x satisfy the Lagrange equations with the
Lagrangian Lc, so the action S'c is stationary with respect to
variations  of x that are zero at the end times:
of x that are zero at the end times:
For realizable paths q the action S[q](t1, t2) is stationary
with respect to variations  of q that are zero at the end
times. Along these paths the momentum py(t) has the constant value
c. For these same paths the action S'c[x](t1, t2) is
stationary with respect to variations
of q that are zero at the end
times. Along these paths the momentum py(t) has the constant value
c. For these same paths the action S'c[x](t1, t2) is
stationary with respect to variations  of x that are zero at
the end times. The dimension of
of x that are zero at
the end times. The dimension of  is smaller than the dimension
of
is smaller than the dimension
of  .
.
The values of the actions S'c[x](t1, t2) and S[q](t1, t2) are
related:
Exercise 3.9. Routhian equations of motion
Verify that the equations of motion are given by
equations (3.113-3.115).
 1 H)i = 0.19
According to Hamilton's equations, the conjugate momentum pi is
conserved. Hamilton's equations of motion for the remaining 2n - 2
phase-space variables do not involve qi (because it does not appear
in the Hamiltonian), and pi is a constant. Thus the dimension of
the difficult part of the problem, the part that involves the solution
of coupled ordinary differential equations, is reduced by two. The
remaining equation governing the evolution of qi in general depends
on all the other variables, but once the reduced problem has been
solved, the equation of motion for qi can be written so as to
give Dqi explicitly as a function of time. We can then find
qi as a definite integral of this function.20
1 H)i = 0.19
According to Hamilton's equations, the conjugate momentum pi is
conserved. Hamilton's equations of motion for the remaining 2n - 2
phase-space variables do not involve qi (because it does not appear
in the Hamiltonian), and pi is a constant. Thus the dimension of
the difficult part of the problem, the part that involves the solution
of coupled ordinary differential equations, is reduced by two. The
remaining equation governing the evolution of qi in general depends
on all the other variables, but once the reduced problem has been
solved, the equation of motion for qi can be written so as to
give Dqi explicitly as a function of time. We can then find
qi as a definite integral of this function.20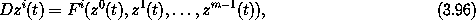

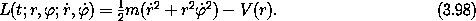
 and p
and p = m r2
= m r2  .
The kinetic energy is a homogeneous quadratic form in the velocities,
so the
.
The kinetic energy is a homogeneous quadratic form in the velocities,
so the 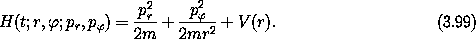
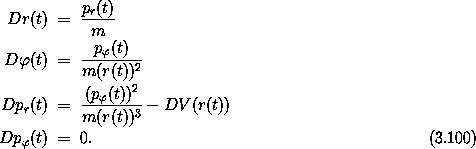
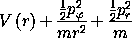

 expresses
a rotation about the symmetry axis. The next Euler angle
expresses
a rotation about the symmetry axis. The next Euler angle  is
the tilt of the symmetry axis of the top from the vertical. The third
Euler angle
is
the tilt of the symmetry axis of the top from the vertical. The third
Euler angle 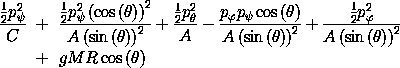
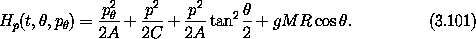
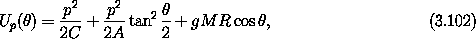

 , where
, where 


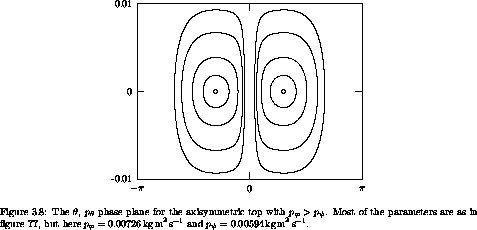
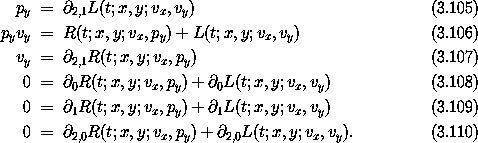
 :
:
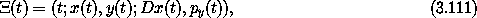
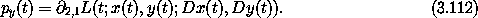
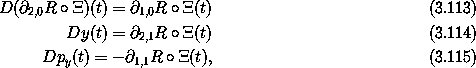


 of x that are zero at the end times:
of x that are zero at the end times:

 of q that are zero at the end
times. Along these paths the momentum py(t) has the constant value
c. For these same paths the action S'c[x](t1, t2) is
stationary with respect to variations
of q that are zero at the end
times. Along these paths the momentum py(t) has the constant value
c. For these same paths the action S'c[x](t1, t2) is
stationary with respect to variations 