Most problems do not have enough symmetries to be reducible to quadrature. It is natural to turn to numerical integration to learn more about the evolution of such systems. The evolution in phase space may be found by numerical integration of Hamilton's equations.
Hamilton's equations are already in first-order form; the Hamiltonian state derivative is the same as the phase-space derivative:
(define Hamiltonian->state-derivative
phase-space-derivative)
As an illustration, consider again the periodically driven pendulum (see section 1.6.2). The Hamiltonian is
(show-expression
((Lagrangian->Hamiltonian
(L-periodically-driven-pendulum 'm 'l 'g 'a 'omega))
(up 't 'theta 'p_theta)))
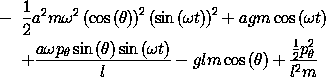
Hamilton's equations for the periodically driven pendulum are unrevealing, so we will not show them. We build a system derivative from the Hamiltonian:
(define (H-pend-sysder m l g a omega)
(Hamiltonian->state-derivative
(Lagrangian->Hamiltonian
(L-periodically-driven-pendulum m l g a omega))))
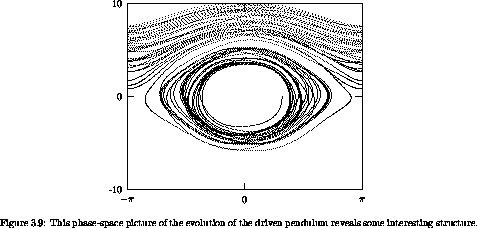
Now we integrate this system, with the same initial conditions as in section 1.7 (see figure 1.7), but displaying the trajectory in phase space (figure 3.9). We make a monitor procedure to display the evolution in phase space:
(define ((monitor-p-theta win) state)
(let ((q ((principal-value :pi) (coordinate state)))
(p (momentum state)))
(plot-point win q p)))
We use evolve to explore the evolution of the system:
(define window (frame :-pi :pi -10.0 10.0))
(let ((m 1.) ;m=1kg
(l 1.) ;l=1m
(g 9.8) ;g=9.8m/s2
(A 0.1) ;A=1/10 m
(omega (* 2 (sqrt 9.8))))
((evolve H-pend-sysder m l g A omega)
(up 0.0 ;t0=0
1.0 ;theta0=1 rad
0.0) ;p0=0 kg m2/s
(monitor-p-theta window)
0.01 ;plot interval
100.0 ;final time
1.0e-12))
The trajectory sometimes oscillates and sometimes circulates. The patterns in the phase plane are reminiscent of the trajectories in the phase plane of the undriven pendulum shown in figure 3.4.
We are familiar with the fact that a given motion of a system is expressed differently in different coordinate systems: the functions that express a motion in rectangular coordinates are different from the functions that express the same motion in polar coordinates. However, in a given coordinate system the evolution of the local state tuple for particular initial conditions is unique. The generalized velocity path function is the derivative of the generalized coordinate path function. On the other hand, the coordinate system alone does not uniquely specify the phase-space description. The relationship of the momentum to the coordinates and the velocities depends on the Lagrangian, and many different Lagrangians may be used to describe the behavior of the same physical system. When two Lagrangians for the same physical system are different, the phase-space descriptions of a dynamical state are different.
We have already seen two different Lagrangians for the driven pendulum
(see section 1.6.4): one was found using L = T - V
and the other was found by inspection of the equations of motion. The
two Lagrangians differ by a total time derivative. The momentum p
conjugate to depends on which Lagrangian we choose
to work with, and the description of the evolution in the
corresponding phase space also depends on the choice of Lagrangian,
even though the behavior of the system is independent of the method
used to describe it. The momentum conjugate to , using the
L = T - V Lagrangian for the periodically driven pendulum, is
and the momentum conjugate to , with the alternate
Lagrangian, is
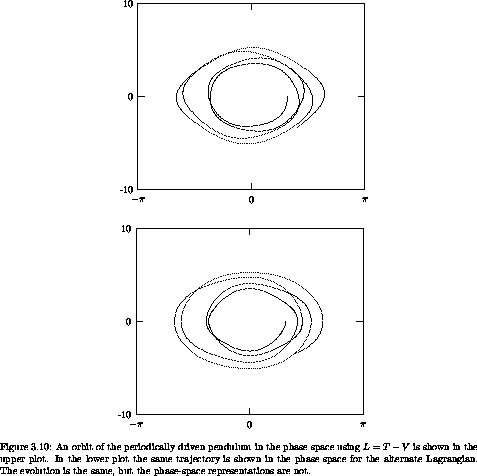
The two momenta differ by an additive distortion that varies
periodically in time and depends on . That the phase-space
descriptions are different is illustrated in
figure 3.10. The evolution of the
system is the same for each.
