
Qualitative changes are associated with fixed points of the surface of section. As the drive is turned on, chaotic zones appear at fixed points on separatrices of the undriven system, and we observe the appearance of new fixed points and periodic points associated with resonance islands. Here we investigate the behavior of systems near fixed points. We can distinguish two types of fixed points on a surface of section: there are fixed points that correspond to equilibria of the system and there are fixed points that correspond to periodic orbits of the system. We first consider the stability of equilibria of systems governed by differential equations, then discuss the stability of fixed points of maps.
Consider first the case of an equilibrium of a system of differential equations. If a system is initially at an equilibrium point, the system remains there. What can we say about the evolution of the system for points near such an equilibrium point? This is actually a very difficult question, which has not been completely answered. We can, however, understand quite a lot about the motion of systems near equilibrium. The first step is to investigate the evolution of a linear approximation to the differential equations near the equilibrium. This part is easy, and is the subject of linear stability analysis. Later, we will address what the linear analysis implies for the actual problem.
Consider a system of ordinary differential equations


where n is the dimension of the state space. An equilibrium point of this system of equations is a point ze for which the state derivative is zero:

That this is zero at all moments for the equilibrium solution implies
 0 F(t, ze) = 0.
0 F(t, ze) = 0.
Next consider a state path z' that passes near the equilibrium point.
The path displacement  is defined so that at time t
is defined so that at time t

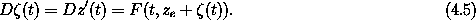
If  is small we can write the right-hand side as a Taylor
series in
is small we can write the right-hand side as a Taylor
series in  :
:
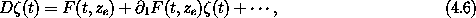
but the first term is zero because ze is an equilibrium point, so

If  is small the evolution is approximated by the
linear terms. Linear stability analysis investigates the evolution of the
approximate equation
is small the evolution is approximated by the
linear terms. Linear stability analysis investigates the evolution of the
approximate equation

These are the variational equations (3.144) with the equilibrium solution substituted for the reference trajectory. The relationship of the solutions of this linearized system to the full system is a difficult mathematical problem, which has not been fully resolved.
If we restrict attention to autonomous systems ( 0 F = 0),
then the variational equations at an equilibrium are a linear system
of ordinary differential equations with constant coefficients.2
Such systems can be solved analytically. To simplify the notation,
let M =
0 F = 0),
then the variational equations at an equilibrium are a linear system
of ordinary differential equations with constant coefficients.2
Such systems can be solved analytically. To simplify the notation,
let M =  1 F(t, ze), so
1 F(t, ze), so

We seek a solution of the form

where  is a structured constant with the same number of
components as
is a structured constant with the same number of
components as  , and
, and  is a complex number called a
characteristic exponent. Substituting, we find
is a complex number called a
characteristic exponent. Substituting, we find

The exponential factor is not zero, so we find

which is an equation for the eigenvalue  and (normalized) eigenvector
and (normalized) eigenvector
 . In general, there are n eigenvalues and n eigenvectors,
so we must add a subscript to both
. In general, there are n eigenvalues and n eigenvectors,
so we must add a subscript to both  and
and  indicating the
particular solution. The general solution is an arbitrary linear
combination of these individual solutions. The eigenvalues are
solutions of the characteristic equation
indicating the
particular solution. The general solution is an arbitrary linear
combination of these individual solutions. The eigenvalues are
solutions of the characteristic equation

where M is the matrix representation of M, and I is
the identity matrix of the same dimension. The elements of M
are real, so we know that the eigenvalues  either are real or
come in complex-conjugate pairs. We assume the eigenvalues are all
distinct.3
either are real or
come in complex-conjugate pairs. We assume the eigenvalues are all
distinct.3
If the eigenvalue is real then the
solution is exponential, as assumed. If the eigenvalue  > 0
then the solution expands exponentially along the direction
> 0
then the solution expands exponentially along the direction
 ; if
; if  < 0 then the solution contracts exponentially
along the direction
< 0 then the solution contracts exponentially
along the direction  .
.
If the eigenvalue is complex we
can form real solutions by combining the two solutions for the
complex-conjugate pair of eigenvalues. Let  = a + i b, with real a
and b, be one such complex eigenvalue. Let
= a + i b, with real a
and b, be one such complex eigenvalue. Let  = u + i v,
where u and v are real, be the eigenvector corresponding to it.
So there is a complex solution of the form
= u + i v,
where u and v are real, be the eigenvector corresponding to it.
So there is a complex solution of the form
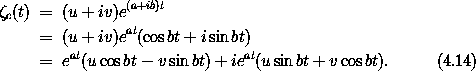
The complex conjugate of this solution is also a solution, because the
ordinary differential equation is linear with real linear
coefficients. This complex-conjugate solution is associated with the
eigenvalue that is the complex conjugate of the original complex
eigenvalue. So the real and imaginary parts of  c are real
solutions:
c are real
solutions:

These two solutions reside in the plane containing the vectors u and v. If a is positive both solutions spiral outwards exponentially, and if a is negative they both spiral inwards. If a is zero, both solutions trace the same ellipse, but with different phases.
Again, the general solution is an arbitrary linear combination of the
particular real solutions corresponding to the various eigenvalues.
So if we denote the kth real eigensolution  k(t), then
the general solution is
k(t), then
the general solution is

where Ak may be determined by the initial conditions (the state at a given time).
Carry out the details of finding the eigensolutions for the two
equilibria of the pendulum ( = 0 and
= 0 and  =
=  , both with
p
, both with
p = 0). How is the small-amplitude oscillation frequency
related to the eigenvalues? How are the eigendirections related to
the contours of the Hamiltonian?
= 0). How is the small-amplitude oscillation frequency
related to the eigenvalues? How are the eigendirections related to
the contours of the Hamiltonian?
Fixed points on a surface of section correspond either to equilibrium points of the system or to a periodic motion of the system. Linear stability analysis of fixed points is similar to the linear stability analysis for equilibrium points.
Let T be a map of the state space onto itself, as might be generated by a surface of section. A trajectory sequence is generated by successive iteration of the map T. Let x(n) be the nth point of the sequence. The map carries one point of the trajectory sequence to the next: x(n + 1) = T(x(n)). We can represent successive iterations of the map by a superscript, so that Ti indicates T composed i times. For example, T2(x) = T(T(x)). Thus x(n) = Tn(x(0)).4
A fixed point x0 of the map T satisfies

A periodic point of the map T is a point that is visited every k iterations of T. Thus it is a fixed point of the map Tk. So the behavior near a periodic point can be ascertained by looking at the behavior near an associated fixed point of Tk.
Let x be some trajectory initially near the fixed point x0 of T, and  be the deviation from x0: x(n) = x0 +
be the deviation from x0: x(n) = x0 +  (n). The
trajectory satisfies
(n). The
trajectory satisfies

Expanding the right-hand side as a Taylor series, we obtain
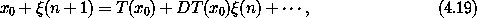

Linear stability analysis considers the evolution of the system truncated to the linear terms

This is a system of linear difference equations, with constant coefficients DT(x0).
We assume there are solutions of the form

where 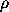 is some (complex) number, called a
characteristic multiplier.5
Substituting this solution into the linearized evolution equation, we find
is some (complex) number, called a
characteristic multiplier.5
Substituting this solution into the linearized evolution equation, we find


where I is the identity function. We see that 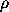 is an eigenvalue of the
linear transformation DT(x0) and
is an eigenvalue of the
linear transformation DT(x0) and  is the associated
(normalized) eigenvector. Let M = DT(x0), and M be its matrix
representation. The eigenvalues are determined by
is the associated
(normalized) eigenvector. Let M = DT(x0), and M be its matrix
representation. The eigenvalues are determined by

The elements of M are real, so the eigenvalues 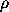 are
either real or come in complex-conjugate pairs.6
are
either real or come in complex-conjugate pairs.6
For the real
eigenvalues the solutions are just exponential expansion or
contraction along the associated eigenvector  :
:

The solution is expanding if || 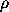 || > 1 and contracting if ||
|| > 1 and contracting if ||
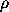 || < 1. If the eigenvalues are complex, then the solution is
complex, but the complex solutions corresponding to the complex-conjugate
pair of eigenvalues can be combined to form two real
solutions, as was done for the equilibrium solutions. Let
|| < 1. If the eigenvalues are complex, then the solution is
complex, but the complex solutions corresponding to the complex-conjugate
pair of eigenvalues can be combined to form two real
solutions, as was done for the equilibrium solutions. Let 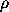 =
exp(A + i B) with real A and B, and
=
exp(A + i B) with real A and B, and  = u + i v. A
calculation similar to that for the equilibrium case show that there
are two real solutions
= u + i v. A
calculation similar to that for the equilibrium case show that there
are two real solutions
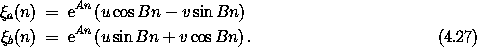
We see that if A>0 then the solution exponentially expands, and if
A<0 the solution exponentially contracts. Exponential expansion,
A>0, corresponds to || 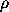 || > 1; exponential contraction, A<0,
corresponds to ||
|| > 1; exponential contraction, A<0,
corresponds to || 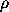 || < 1. If A = 0 then the two real solutions
trace an ellipse and any linear combination of them traces an ellipse.
|| < 1. If A = 0 then the two real solutions
trace an ellipse and any linear combination of them traces an ellipse.
The general solution is an arbitrary linear combination of each of the
eigensolutions. Let  k be the kth real eigensolution.
The general solution is
k be the kth real eigensolution.
The general solution is

where Ak may be determined by the initial conditions.
Exercise 4.2. Elliptical oscillation
Show that the arbitrary linear combination of  a and
a and  b
traces an ellipse for A = 0.
b
traces an ellipse for A = 0.
The standard map (see section 3.9) has fixed points
at I = 0 for  = 0 and
= 0 and  =
=  . Find the full
eigensolutions for these two fixed points. For what ranges of the
parameter K are the fixed points linearly stable or unstable?
. Find the full
eigensolutions for these two fixed points. For what ranges of the
parameter K are the fixed points linearly stable or unstable?
For maps that are generated by stroboscopic sampling of the evolution
of a system of autonomous differential equations, equilibrium points
are fixed points of the map. The eigensolutions of the equilibrium of
the flow and the eigensolutions of the map at the fixed point are then
related. Let  be the sampling period. Then
be the sampling period. Then
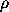 i = e
i = e i
i  .
.
The Lyapunov exponent is a measure of the rate of exponential
divergence of nearby trajectories from a reference trajectory. If the
reference trajectory is an equilibrium of a flow, then the Lyapunov
exponents are the real parts of the linearized characteristic
exponents  i. If the reference trajectory is fixed point of
a map generated by a flow (either a periodic orbit or an equilibrium),
then the Lyapunov exponents are real parts of the logarithm of the
characteristic multipliers, divided by the period of the map. So if
the characteristic multiplier is
i. If the reference trajectory is fixed point of
a map generated by a flow (either a periodic orbit or an equilibrium),
then the Lyapunov exponents are real parts of the logarithm of the
characteristic multipliers, divided by the period of the map. So if
the characteristic multiplier is 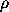 = eA+iB and the period of
the map is
= eA+iB and the period of
the map is  , then the Lyapunov exponent is A/
, then the Lyapunov exponent is A/ . A positive
Lyapunov exponent of a fixed point indicates linear instability of the
fixed point.
. A positive
Lyapunov exponent of a fixed point indicates linear instability of the
fixed point.
The Lyapunov exponent has less information than the characteristic multipliers or exponents because the imaginary part is lost. However, the Lyapunov exponent is more generally applicable in that it is well defined even for reference trajectories that are not periodic.
In the linear analysis of the fixed point, each characteristic exponent corresponds to a subspace of possible linear solutions. For instance, for a real characteristic multiplier there is a corresponding eigendirection, and for any initial displacement along this direction successive iterates are also along this direction. Complex-conjugate pairs of multipliers correspond to a plane of solutions. For a displacement initially on this plane, successive iterates are also on this plane.
It turns out that something like this is also the case for the linearized solutions near a reference trajectory that is not at a fixed point. For each nonzero Lyapunov exponent there is a twisting subspace, so that for an initial displacement in this subspace successive iterates also belong to the subspace. At different points along the reference trajectory the unit displacement vector that characterizes the direction of this subspace is different.
For Hamiltonian systems there are additional constraints among the eigenvalues.
Consider first the case of two-dimensional surfaces of section. We
have seen that Hamiltonian surfaces of section preserve area.
As we saw in the proof of Liouville's theorem, area preservation
implies that the determinant of the derivative of the transformation
is 1. At a fixed point x0 the linearized map is  (n + 1) =
DT(x0)
(n + 1) =
DT(x0)  (n). So M = DT(x0) has unit determinant. Now the
determinant is the product of the eigenvalues, so for a fixed point on
a Hamiltonian surface of section the two eigenvalues must be inverses
of each other. We also have the constraint that if an eigenvalue is
complex then the complex conjugate of the eigenvalue is also an
eigenvalue. These two conditions imply that the eigenvalues must
either be real and inverses, or be complex-conjugate pairs on the unit
circle (see figure 4.4).
(n). So M = DT(x0) has unit determinant. Now the
determinant is the product of the eigenvalues, so for a fixed point on
a Hamiltonian surface of section the two eigenvalues must be inverses
of each other. We also have the constraint that if an eigenvalue is
complex then the complex conjugate of the eigenvalue is also an
eigenvalue. These two conditions imply that the eigenvalues must
either be real and inverses, or be complex-conjugate pairs on the unit
circle (see figure 4.4).
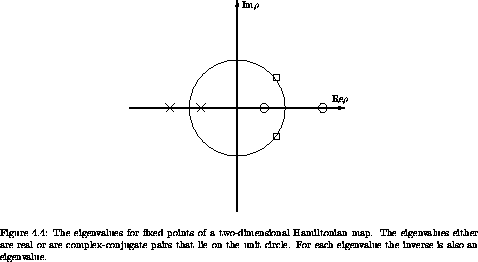
Fixed points for which the characteristic multipliers all lie on the unit circle are called elliptic fixed points. The solutions of the linearized variational equations trace ellipses around the fixed point. Elliptic fixed points are linearly stable.
Fixed points with positive real characteristic multipliers are called hyperbolic fixed points. For two-dimensional maps, there is an exponentially expanding subspace and an exponentially contracting subspace. The general solution is a linear combination of these. Fixed points for which the characteristic multipliers are negative are called hyperbolic with reflection.
The edge case of two degenerate characteristic multipliers is called parabolic. For two degenerate eigenvalues the general solution grows linearly. This happens at points of bifurcation where elliptic points become hyperbolic points or vice versa.
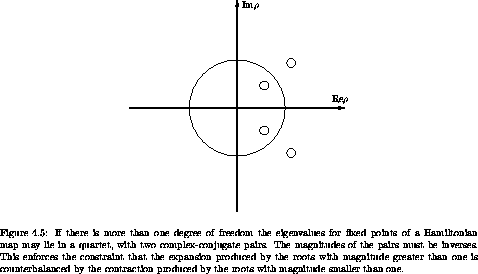
For two-dimensional Hamiltonian maps these are the only possibilities. For higher-dimensional Hamiltonian maps, we can get combinations of these: some characteristic multipliers can be real and others complex-conjugate pairs. We might imagine that in addition there would be many other types of fixed points that occur in higher dimensions. In fact, there is only one additional type, shown in figure 4.5. For Hamiltonian systems of arbitrary dimensions it is still the case that for each eigenvalue the complex conjugate and the inverse are also eigenvalues. We can prove this starting from a result in chapter 5. Consider the map of the phase space onto itself that is generated by time evolution of a Hamiltonian system. Let z = (q, p); then the map Tß satisfies z(t + ß) = Tß(z(t)) for solutions z of Hamilton's equations. We will show in chapter 5 that the derivative of the map Tß is symplectic, whether or not the starting point is at a fixed point. A 2n×2n matrix M is symplectic if it satisfies

where J is the 2n-dimensional symplectic unit:

with the n× n unit matrix 1n × n and the n × n zero matrix 0n × n.
Using the symplectic property, we can show that in general for each
eigenvalue its inverse is also an eigenvalue. Assume 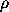 is an
eigenvalue, so that
is an
eigenvalue, so that 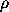 satisfies det(M -
satisfies det(M - 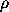 I) = 0.
This equation is unchanged if M is replaced by its transpose,
so
I) = 0.
This equation is unchanged if M is replaced by its transpose,
so 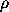 is also an eigenvalue of MT:
is also an eigenvalue of MT:


Now, from the symplectic property we have


and we can conclude that 1/ is an eigenvalue of M with the
eigenvector J
is an eigenvalue of M with the
eigenvector J  '. From the fact that for every
eigenvalue its inverse is also an eigenvalue we deduce that the
determinant of the transformation M, which is the product of
the eigenvalues, is one.
'. From the fact that for every
eigenvalue its inverse is also an eigenvalue we deduce that the
determinant of the transformation M, which is the product of
the eigenvalues, is one.
The constraints that the eigenvalues must be associated with inverses and complex conjugates yields exactly one new pattern of eigenvalues in higher dimensions. Figure 4.5 shows the only new pattern that is possible.
We have seen that the Lyapunov exponents for fixed points are related to the characteristic multipliers for the fixed points, so the Hamiltonian constraints on the multipliers correspond to Hamiltonian constraints for Lyapunov exponents at fixed points. For each characteristic multiplier, the inverse is also a characteristic multiplier. This means that at fixed points, for each positive Lyapunov exponent there is a corresponding negative Lyapunov exponent with the same magnitude. It turns out that this is also true if the reference trajectory is not at a fixed point. For Hamiltonian systems, for each positive Lyapunov exponent there is a corresponding negative exponent of equal magnitude.
Describe (perhaps by drawing cross sections) the orbits that are possible with quartets.
A fixed point that is linearly unstable indicates that the full system is unstable at that point. This means that trajectories starting near the fixed point diverge from the fixed point. On the other hand, linear stability of a fixed point does not generally guarantee that the full system is stable at that point. For a two-degree-of-freedom Hamiltonian system, the Kolmogorov-Arnold-Moser theorem proves under certain conditions that linear stability implies nonlinear stability. In higher dimensions, though, it is not known whether linear stability implies nonlinear stability.
2 Actually, all we need is  0
0  1 F(t, ze) = 0.
1 F(t, ze) = 0.
3 If the eigenvalues are not unique then the form of the solution is modified.
4 The map T is being used as an operator: multiplication is interpreted as composition.
5 A characteristic multiplier is also sometimes called a Floquet multiplier.
6 We assume for now that the eigenvalues are distinct.