3.9  Standard Map

We have seen that the surfaces of section for a number of different problems are qualitatively very similar. They all show two qualitatively different types of motion: regular motion and chaotic motion. They show that these types of orbits are clustered: there are regions of the surface of section that have mostly regular trajectories and other regions dominated by chaotic behavior. We have also seen a transition to large-scale chaotic behavior as some parameter is varied. Now we have learned that the map that takes points on a two-dimensional surface of section to new points on the surface of section is area preserving. The sole property that these maps of the section onto itself have in common (that we know of at this point) is that they preserve area. Otherwise they are quite distinct. Suppose we consider an abstract map of the section onto itself that is area preserving, without regard for whether the map is generated by some dynamical system. Do area-preserving maps show similar phenomena, or is the dynamical origin of the map crucial to the phenomena we have found?³⁴

Consider a map of the phase plane onto itself defined in terms of the dynamical variables and its ``conjugate momentum'' I. The map is

This map is known as the ``standard map.''³⁵ A curious feature of the standard map is that the momentum variable I is treated as an angular quantity. The derivative of the map has determinant one, implying the map is area preserving.

We can implement the standard map:

(define ((standard-map K) theta I return failure)
  (let ((nI (+ I (* K (sin theta)))))
    (return ((principal-value :2pi) (+ theta nI))
            ((principal-value :2pi) nI))))

We use the explore-map procedure introduced earlier to use a pointing device to interactively explore the surface of section. For example, to explore the surface of section for parameter K = 0.6 we use:

(define window (frame 0.0 :2pi 0.0 :2pi))
(explore-map window (standard-map 0.6) 2000)

The resulting surface of section, for a variety of orbits chosen with the pointer, is shown in figure 3.27.

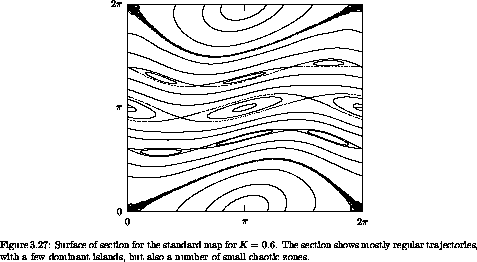
The surface of section does indeed look qualitatively similar to the surfaces of section generated by dynamical systems.

The surface of section for K = 1.4 (as shown in figure 3.28) is dominated by a large chaotic zone. The standard map exhibits a transition to large-scale chaos near K = 1. So this abstract area-preserving map of the phase plane onto itself shows behavior that is similar to behavior in the sections generated by a Hamiltonian dynamical system. Evidently, the area-preservation property of the dynamics in the phase space plays a determining role for many interesting properties of trajectories of mechanical systems.

Exercise 3.13.  Fun with Hénon's quadratic map
Consider the map of the plane defined by the equations:

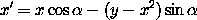
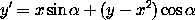
a.  Show that the map preserves area.

b.  Implement the map as a procedure. The interesting range of x and y is ( - 1, 1). There will be orbits that escape. You should check for values of x and y that escape from this range and call the failure continuation when this occurs.

c.  Explore the phase portrait of this map for a few values of the parameter 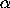. The map is particularly interesting for 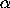= 1.32 and 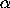= 1.2. What happens in between?