3.8  Liouville's Theorem

If an ensemble of states occupies a particular volume of phase space at one moment, then the subsequent evolution of that volume by the flow described by Hamilton's equations may distort the ensemble but does not change the volume the ensemble occupies. The fact that phase-space volume is preserved by the phase flow is called Liouville's theorem.

We will first illustrate the preservation of phase-space volume with a simple example and then prove it in general.

The phase flow for the pendulum

Consider an undriven pendulum described by the Hamiltonian:

In figure 3.25 we see the evolution of an elliptic region around a point on the -axis, in the oscillation region of the pendulum. Three later positions of the region are shown. The region is stretched and sheared by the flow, but the area is preserved. After many cycles, the starting region will be stretched to be a thin layer distributed in the phase angle of the pendulum.

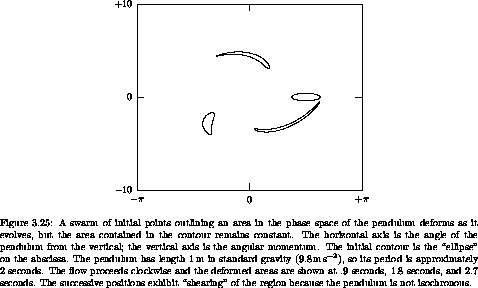
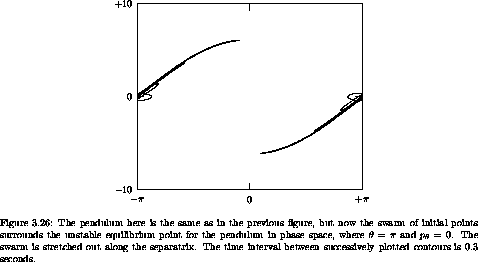
Figure 3.26 shows a similar evolution (for smaller time intervals) of a region straddling the separatrix³¹ near the unstable equilibrium point. The phase-space region rapidly stretches along the separatrix, while preserving the area. The initial conditions that start in the oscillation region (inside of the separatrix) will continue to spread into a thin ring-shaped region, while the initial conditions that start outside of the separatrix will spread into a thin region of rotation on the outside of the separatrix.

Proof of Liouville's theorem

Consider a set of ordinary differential equations of the form

where z is a tuple of N state variables. Let R(t₁) be a region of the state space at time t₁. Each element of this region is an initial condition at time t₁ for the system, and evolves to an element at time t₂ according to the differential equations. The set of these elements at time t₂ is the region R(t₂). Regions evolve to regions.

The evolution of the system for a time interval t defines a map g_{t, t} from the state space to itself:

Regions map to regions by mapping each element in the region:

The volume V(t) of a region R(t) is _R(t) , where 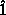is the function whose value is one for every input. The volume of the evolved region R(t + t) is

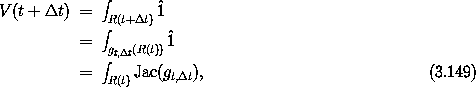
where Jac(g_{t, t}) is the Jacobian of the mapping g_{t, t}. The Jacobian is the determinant of the derivative of the mapping.

For small t

and thus

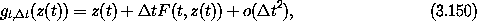
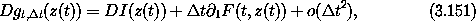
where I is the identity function, so DI(z(t)) is a unit multiplier. We can use the fact that if A is an N × N square matrix then

to show that

where

Thus

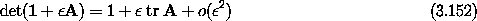
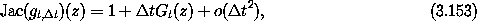
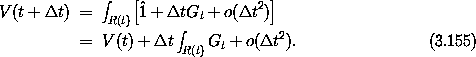
So the rate of change of the volume at time t is

Now we compute G_t for a system described by a Hamiltonian H. The components of z are the components of the coordinates and the momenta: z^k = q^k, z^k+n = p_k for k = 0, ..., n - 1. The components of F are

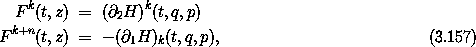
for k = 0, ..., n - 1. The diagonal components of the derivative ₁ F are

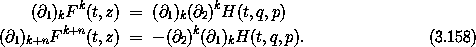
The component partial derivatives commute, so the diagonal components with index k and index k + n are equal and opposite. We see that the trace, which is the sum of these diagonal components, is zero. Thus the integral of G_t over the region R(t) is zero, so the derivative of the volume at time t is zero. Because t is arbitrary, the volume does not change. This proves Liouville's theorem: the phase-space flow conserves phase-space volume.

Notice that the proof of Liouville's theorem does not depend upon whether or not the Hamiltonian has explicit time dependence. Liouville's theorem holds for systems with time-dependent Hamiltonians.

We may think of the ensemble of all possible states as a fluid flowing around under the control of the dynamics. Liouville's theorem says that this fluid is incompressible for Hamiltonian systems.

Exercise 3.11.  Determinants and traces
Show that equation (3.152) is correct.

Area preservation of stroboscopic surfaces of section

Surfaces of section for periodically driven Hamiltonian systems are area preserving if the section coordinates are the phase-space coordinate and momentum. This is an important feature of surfaces of section. It is a consequence of Liouville's theorem for one-degree-of-freedom problems.

It is also the case that surfaces of section such as those we have used for the Hénon-Heiles problem are area preserving, but we are not ready to prove this yet!

Poincaré recurrence

The Poincaré recurrence theorem is a remarkable theorem that is a trivial consequence of Liouville's theorem. Loosely, the theorem states that almost all trajectories eventually return arbitrarily close to where they started. This is true regardless of whether the trajectories are chaotic or regular.

More precisely, consider a Hamiltonian dynamical system for which the phase space is a bounded domain D. We identify some initial point in the phase space, say z₀. Then, for any finite neighborhood U of z₀ we choose, there are trajectories that emanate from initial points in that neighborhood and eventually return to the neighborhood.

We can prove this by considering the successive images of U under the time evolution. For simplicity, we restrict consideration to time evolution for a time interval . The map of the phase space onto itself generated by time evolution for an interval we call C. Subsequent applications of the map generate a discrete time evolution. Sets of points in phase space transform by evolving all the points in the set; the image of the set U is denoted C(U). Now consider the trajectory of the set U, that is, the sets Cⁿ(U) where Cⁿ indicates the n-times composition of C. Now there are two possibilities: either the successive images Cⁱ(U) intersect or they do not. If they do not intersect, then with each iteration, a volume of D equal to the volume of U gets ``used up'' and cannot belong to the further image. But the volume of D is finite, so we cannot fit an infinite number of non-intersecting finite volumes into it. Therefore, after some number of iterations the images intersect. Suppose Cⁱ(U) intersects with C^j(U), with j<i, for definiteness. Then the pre-image of each must also intersect, since the pre-image of a point in the intersection belongs to both sets. Thus C^i-1(U) intersects C^j-1(U). This can be continued until finally we have that C^i-j(U) intersects U. So we have proven that after i - j iterations of the map C there are a set of points initially in U that return to the neighborhood U.

So for every neighborhood of every point in the phase space there is a subneighborhood such that the trajectories emanating from all of the points in that subneighborhood return to that subneighborhood. Thus almost every trajectory returns arbitrarily close to where it started.

The gas in the corner of the room

Suppose we have a collection of N classical atoms in a perfectly sealed room. The phase-space dimension of this system is 6N. A point in this phase space is denoted z. Suppose initially all the atoms are, say, within one centimeter of one corner, with arbitrarily chosen finite velocities. This corresponds to some initial point z₀ in the phase space. The phase space of the system is limited in space by the room and in momentum by energy conservation; the phase space is bounded. The recurrence theorem then says that in the neighborhood of z₀ there is an initial condition of the system that returns to the neighborhood of z₀ after some time. For the individual atoms this means that after some time all of the atoms will be found in the corner of the room again, and again, and again. Makes one wonder about the second law of thermodynamics, doesn't it?³²

Nonexistence of attractors in Hamiltonian systems

Some systems have attractors. An attractor is a region of phase space that gobbles volumes of trajectories. For an attractor there is some larger region, the basin of attraction, such that sets of trajectories with nonzero volume eventually end up in the attractor and never leave it. The recurrence theorem shows that Hamiltonian systems with bounded phase space do not have attractors. Consider some candidate volume in the proposed basin of attraction. The recurrence theorem guarantees that some trajectories in the candidate volume return to the volume repeatedly. Therefore, the volume is not in a basin of attraction. Attractors do not exist in Hamiltonian systems with bounded phase space.

This does not mean that every trajectory always returns. A simple example is the pendulum. Suppose we take a blob of trajectories that spans the separatrix, the trajectory that asymptotically approaches the unstable equilibrium with the pendulum pointed up. Trajectories with more energy than the separatrix make a full loop around and return to their initial point; trajectories with lower energy than the separatrix oscillate once across and back to their initial position; but the separatrix trajectory itself leaves the initial region permanently, and continually approaches the unstable point.

Conservation of phase volume in a dissipative system

The definition of a dissipative system is not so clear. For some, ``dissipative'' implies that phase-space volume is not conserved, which is the same as saying the evolution of the system is not governed by Hamilton's equations. For others, ``dissipative'' implies that friction is present, representing loss of energy to unmodeled degrees of freedom. Here is a curious example. The damped harmonic oscillator is the paradigm of a dissipative system. Here we show that the damped harmonic oscillator can be described by Hamilton's equations and that phase-space volume is conserved.

The damped harmonic oscillator is governed by the ordinary differential equation

where is a coefficient of damping. We can formulate this system with the Lagrangian³³

The Lagrange equation for this Lagrangian is

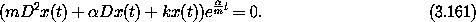
Since the exponential is never zero this equation has the same trajectories as equation (3.159) above.

The momentum conjugate to x is

and the Hamiltonian is

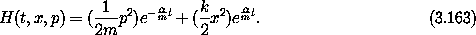
For this system, the Hamiltonian is not the sum of the kinetic energy of the motion of the mass and the potential energy stored in the spring. The value of the Hamiltonian is not conserved (₀ H ne 0). Hamilton's equations are

Let's consider a numerical case. Let m = 5, k = 1/4, = 3. Here the characteristic roots of the linear constant-coefficient ordinary differential equation (3.159) are s = - 1/10, - 1/2. Thus the solutions are

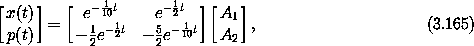
for A₁ and A₂ determined by the initial conditions

Thus we can form the transformation from the initial state to the final state:

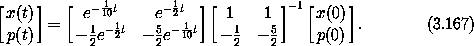
The transformation is linear, so the area is transformed by the determinant, which is 1 in this case. Thus, contrary to intuition, the phase-space volume is conserved. So why is this not a contradiction with the statement that there are no attractors in Hamiltonian systems? The answer is that the Poincaré recurrence argument is true only for bounded phase spaces. Here, the momentum expands exponentially with time (as the coordinate contracts), so it is unbounded.

We shouldn't really be too surprised by the way the theory protects itself from an apparent paradox -- that the phase volume is conserved even though all trajectories decay to zero velocity and coordinates. The proof of Liouville's theorem allows time-dependent Hamiltonians. In this case we are able to model the dissipation by just such a time-dependent Hamiltonian.

Exercise 3.12.  Time-dependent systems
To make the fact that Liouville's theorem holds for time-dependent systems even more concrete, extend the results of section 3.8 to show how a swarm of initial points outlining an area in the phase space of the driven pendulum deforms as it evolves. Construct pictures analogous to figures 3.25 and 3.26 for one of the interesting cases where we have surfaces of section. Does the distortion look different in different parts of the phase space? How?

Distribution functions

We know the state of a system only approximately. It is reasonable to model our state of knowledge by a probability density function on the set of possible states. Given such incomplete knowledge, what are the probable consequences? As the system evolves, the density function also evolves. Liouville's theorem gives us a handle on this kind of problem.

Let f(t, q, p) be a probability density function on the phase space at time t. For this to be a good probability density function we require that the integral of f over all coordinates and momenta be 1 -- it is certain that the system is somewhere.

There is a set of trajectories that pass through any particular region of phase space at a particular time. These trajectories are neither created nor destroyed, and they proceed as a bundle to another region of phase space at a later time. Liouville's theorem tells us that the volume of the source region is the same as the volume of the target region, so the density must remain constant. Thus D(fo) = 0. If we have a system described by the Hamiltonian H then

so we may conclude that

or

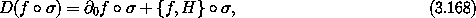
Since this must be true at each moment and since there is a solution trajectory that emanates from every point in phase space, we may abstract from solution paths and deduce a constraint on f:

This linear partial differential equation governs the evolution of the density function, and thus shows how our state of knowledge evolves.