Hénon and Heiles discovered that the chaotic trajectories had remarkable sensitivity to small changes in initial conditions -- initially nearby chaotic trajectories separate roughly exponentially with time. On the other hand, regular trajectories do not exhibit this sensitivity -- initially nearby regular trajectories separate roughly linearly with time.
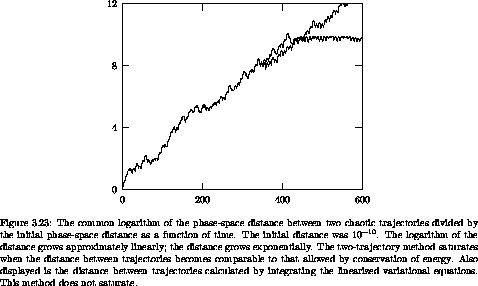
Consider the evolution of two initially nearby trajectories for the Hénon-Heiles problem, with energy E = 1/8. Let d(t) be the usual Euclidean distance in the x, y, px, py space between the two trajectories at time t. Figure 3.23 shows the common logarithm of d(t)/d(0) as a function of time t. We see that the divergence is well described as exponential.

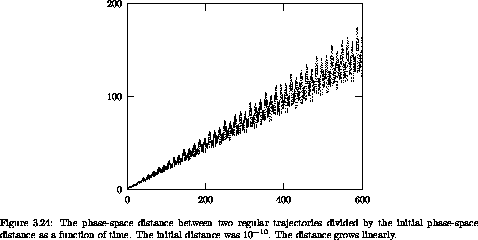
On the other hand, the distance between two initially nearby regular trajectories grows much more slowly. Figure 3.24 shows the distance between two regular trajectories as a function of time. The distance grows linearly with time.
It is remarkable that Hamiltonian systems have such radically different types of trajectories. On the surface of section the chaotic and regular trajectories differ in the dimension of the space that they explore. It is interesting that along with this dimensional difference there is a drastic difference in the way chaotic and regular trajectories separate. For higher dimensional systems the surface of section technique is not as useful, but trajectories are still distinguished by the way neighboring trajectories diverge: some diverge exponentially whereas others diverge approximately linearly. Exponential divergence is the hallmark of chaotic behavior.
The rate of exponential divergence is quantified by the slope of the
graph of log(d(t)/d(0)). We can estimate the rate of exponential
divergence of trajectories from a particular phase-space trajectory
 by choosing a nearby trajectory
by choosing a nearby trajectory  ' and computing
' and computing

where d(t) = ||  '(t) -
'(t) -  (t) ||.
A problem with this ``two-trajectory'' method is
illustrated in figure 3.23. For strongly chaotic
trajectories two initially nearby trajectories soon find themselves as
far apart as they can get. Once this happens the distance no longer
grows. The estimate of the rate of divergence of trajectories is
limited by this ``saturation.''
(t) ||.
A problem with this ``two-trajectory'' method is
illustrated in figure 3.23. For strongly chaotic
trajectories two initially nearby trajectories soon find themselves as
far apart as they can get. Once this happens the distance no longer
grows. The estimate of the rate of divergence of trajectories is
limited by this ``saturation.''
We can improve on this method by studying a variational system of equations. Let

be the system of equations governing the evolution of the system. A nearby trajectory z' satisfies

The difference  = z' - z between these trajectories satisfies
= z' - z between these trajectories satisfies
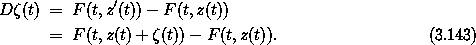
If  is small we can approximate the right-hand side by a derivative
is small we can approximate the right-hand side by a derivative

This set of ordinary differential equations is called the variational
equations for the system. It is linear in  and driven by z.
and driven by z.
Let d(t) = ||  (t) ||; then the rate of divergence can be estimated
as before. The advantage of this ``variational method'' is that
(t) ||; then the rate of divergence can be estimated
as before. The advantage of this ``variational method'' is that  (t)
can become arbitrarily large and its growth still measures the
divergence of nearby trajectories. We can see in
figure 3.23 that the variational method gives
nearly the same result as the two-trajectory method up to the point at
which the two-trajectory method saturates.30
(t)
can become arbitrarily large and its growth still measures the
divergence of nearby trajectories. We can see in
figure 3.23 that the variational method gives
nearly the same result as the two-trajectory method up to the point at
which the two-trajectory method saturates.30
The Lyapunov exponent is defined to be the infinite time limit of  (t),
defined by equation (3.140), in which the
distance d is computed by the variational method. Actually, for each
trajectory there are many Lyapunov exponents, depending on the initial
direction of the variation
(t),
defined by equation (3.140), in which the
distance d is computed by the variational method. Actually, for each
trajectory there are many Lyapunov exponents, depending on the initial
direction of the variation  . For an N-dimensional system,
there are N Lyapunov exponents. For a randomly chosen
. For an N-dimensional system,
there are N Lyapunov exponents. For a randomly chosen  (t0),
the subsequent growth of
(t0),
the subsequent growth of  (t) has components that grow with each of
the Lyapunov exponents. In general, however, the growth of
(t) has components that grow with each of
the Lyapunov exponents. In general, however, the growth of  (t) will
be dominated by the largest exponent. The largest Lyapunov exponent
thus can be interpreted as the typical rate of exponential
divergence of nearby trajectories. The sum of the largest two
Lyapunov exponents can be interpreted as the typical rate of growth of
the area of two-dimensional elements. This interpretation can be extended to
higher-dimensional elements: the rate of growth of volume elements is the
sum of all the Lyapunov exponents.
(t) will
be dominated by the largest exponent. The largest Lyapunov exponent
thus can be interpreted as the typical rate of exponential
divergence of nearby trajectories. The sum of the largest two
Lyapunov exponents can be interpreted as the typical rate of growth of
the area of two-dimensional elements. This interpretation can be extended to
higher-dimensional elements: the rate of growth of volume elements is the
sum of all the Lyapunov exponents.
In Hamiltonian systems, the Lyapunov
exponents must satisfy constraints, which we will justify later. Lyapunov
exponents come in pairs: for every Lyapunov exponent  its
negation -
its
negation -  is also an exponent. For every conserved
quantity, one of the Lyapunov exponents is zero, as is its negation.
So the Lyapunov exponents can be used to check for the existence of
conserved quantities. The sum of the Lyapunov exponents for a
Hamiltonian system is zero, so volume elements do not grow exponentially.
We will see in the next section that phase-space volume is
actually conserved for Hamiltonian systems.
is also an exponent. For every conserved
quantity, one of the Lyapunov exponents is zero, as is its negation.
So the Lyapunov exponents can be used to check for the existence of
conserved quantities. The sum of the Lyapunov exponents for a
Hamiltonian system is zero, so volume elements do not grow exponentially.
We will see in the next section that phase-space volume is
actually conserved for Hamiltonian systems.
30 In strongly chaotic systems  (t) may become so
large that the computer can no longer represent it. To prevent this
we can replace
(t) may become so
large that the computer can no longer represent it. To prevent this
we can replace  by
by  /c whenever
/c whenever  (t) becomes
uncomfortably large. The equation governing
(t) becomes
uncomfortably large. The equation governing  is linear, so except
for the scale change, the evolution is unchanged. Of course we have
to keep track of these scale changes when computing the average growth
rate. This process is called ``renormalization'' to make it sound
impressive.
is linear, so except
for the scale change, the evolution is unchanged. Of course we have
to keep track of these scale changes when computing the average growth
rate. This process is called ``renormalization'' to make it sound
impressive.