Exercise 6.4. Periodically driven pendulum
a. Work out the details of the perturbation theory for the
primary driven pendulum resonances, as displayed in
figure 6.10.
b. Work out the details of the perturbation theory for the stability of the inverted vertical equilibrium. Derive the resonance Hamiltonian and plot its contours. Compare these contours to surfaces of section for a variety of parameters.
c. Carry out the linear stability analysis leading to equation (6.87). What is happening in the upper part of figure 6.15? Why is the system unstable when criterion (6.87) predicts stability? Use surfaces of section to investigate this parameter regime.
Exercise 6.5. Spin-orbit coupling
A Hamiltonian for the spin-orbit problem described in
section 2.11.2 is
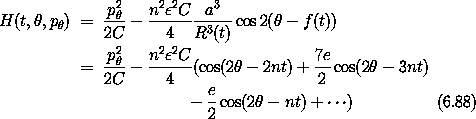
where the ignored terms are higher order in eccentricity e.
a. Find the widths and centers of the three primary resonances. Compare the predictions for the widths to the island widths seen on surfaces of section. Write the criterion for resonance overlap and compare to numerical experiments for the transition to large-scale chaos.
b. The fixed point of the synchronous island is offset from the average rate of rotation. This is indicative of a ``forced'' oscillation of the rotation of the Moon. Develop a perturbative theory for motion in the synchronous island by using a Lie transform to eliminate the two non-synchronous resonances. Predict the location of the fixed point at the center of the synchronous resonance on the surface of section, and thus predict the amplitude of the forced oscillation of the Moon.