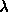 -expressions to name procedures.4
For example, the procedure that squares its input can be written:
-expressions to name procedures.4
For example, the procedure that squares its input can be written:
|
Programming languages should be designed not by piling feature on top of
feature, but by removing the weaknesses and restrictions that make additional
features appear necessary. Scheme demonstrates that a very small number
of rules for forming expressions, with no restrictions on how they are
composed, suffice to form a practical and efficient programming language
that is flexible enough to support most of the major programming
paradigms in use today.
IEEE Standard for the Scheme Programming Language [24], p. 3 |
Here we give an elementary introduction to Scheme.1 For a more precise explanation of the language see the IEEE standard [24]; for a longer introduction see the textbook [1].
Scheme is a simple programming language based on expressions. An expression names a value. For example, the numeral 3.14 names an approximation to a familiar number. There are primitive expressions, such as a numeral, that we directly recognize, and there are compound expressions of several kinds.
A procedure call is a kind of compound expression. A procedure call is a sequence of expressions delimited by parentheses. The first subexpression in a procedure call is taken to name a procedure, and the rest of the subexpressions are taken to name the arguments to that procedure. The value produced by the procedure when applied to the given arguments is the value named by the procedure call. For example,
(+ 1 2.14)
3.14
(+ 1 (* 2 1.07))
3.14
are both compound expressions that name the same number as the numeral 3.14.2 In these cases the symbols + and * name procedures that add and multiply, respectively. If we replace any subexpression of any expression with an expression that names the same thing as the original subexpression, the thing named by the overall expression remains unchanged. In general, a procedure call is written
( operator operand-1 ... operand-n )
where operator names a procedure and operand-i names the ith argument.3
Just as we use numerals to name numbers, we use
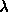 -expressions to name procedures.4
For example, the procedure that squares its input can be written:
-expressions to name procedures.4
For example, the procedure that squares its input can be written:
(lambda (x) (* x x))
This expression can be read: ``The procedure of one argument, x, that multiplies x by x.'' Of course, we can use this expression in any context where a procedure is needed. For example,
((lambda (x) (* x x)) 4)
16
The general form of a 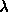 -expression is
-expression is
(lambda formal-parameters body)
where formal-parameters is a list of symbols that will be the names of the arguments to the procedure and body is an expression that may refer to the formal parameters. The value of a procedure call is the value of the body of the procedure with the arguments substituted for the formal parameters.
We can use the define construct to give a name to any object. For example, if we make the definitions5
(define pi 3.141592653589793)
(define square (lambda (x) (* x x)))
we can then use the symbols pi and square wherever the
numeral or the 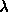 -expression could appear. For example, the
area of the surface of a sphere of radius 5 meters is
-expression could appear. For example, the
area of the surface of a sphere of radius 5 meters is
(* 4 pi (square 5))
314.1592653589793
Procedure definitions may be expressed more conveniently using ``syntactic sugar.'' The squaring procedure may be defined
(define (square x) (* x x))
which we may read: ``To square x multiply x by x.''
In Scheme, procedures may be passed as arguments and returned as values. For example, it is possible to make a procedure that implements the mathematical notion of the composition of two functions:6
(define compose
(lambda (f g)
(lambda (x)
(f (g x)))))
((compose square sin) 2)
.826821810431806
(square (sin 2))
.826821810431806
Using the syntactic sugar shown above, we can write the definition more conveniently. The following are both equivalent to the definition above:
(define (compose f g)
(lambda (x)
(f (g x))))
(define ((compose f g) x)
(f (g x)))
Conditional expressions may be used to choose among several expressions to produce a value. For example, a procedure that implements the absolute value function may be written:
(define (abs x)
(cond ((< x 0) (- x))
((= x 0) x)
((> x 0) x)))
The conditional cond takes a number of clauses. Each clause has a predicate expression, which may be either true or false, and a consequent expression. The value of the cond expression is the value of the consequent expression of the first clause for which the corresponding predicate expression is true. The general form of a conditional expression is
(cond (predicate-1 consequent-1)
···
(predicate-n consequent-n))
For convenience there is a special predicate expression else that can be used as the predicate in the last clause of a cond. The if construct provides another way to make a conditional when there is only a binary choice to be made. For example, because we have to do something special only when the argument is negative, we could have defined abs as:
(define (abs x)
(if (< x 0)
(- x)
x))
The general form of an if expression is
(if predicate consequent alternative)
If the predicate is true the value of the if expression is the value of the consequent, otherwise it is the value of the alternative.
Given conditionals and definitions, we can write recursive procedures. For example, to compute the nth factorial number we may write:
(define (factorial n)
(if (= n 0)
1
(* n (factorial (- n 1)))))
(factorial 6)
720
(factorial 40)
815915283247897734345611269596115894272000000000
The let expression is used to give names to objects in a local context. For example,
(define (f radius)
(let ((area (* 4 pi (square radius)))
(volume (* 4/3 pi (cube radius))))
(/ volume area)))
(f 3)
1
The general form of a let expression is
(let ((variable-1 expression-1)
···
(variable-n expression-n))
body)
The value of the let expression is the value of the body expression in the context where the variables variable-i have the values of the expressions expression-i. The expressions expression-i may not refer to any of the variables.
A slight variant of the let expression provides a convenient way to express looping constructs. We can write a procedure that implements an alternative algorithm for computing factorials as follows:
(define (factorial n)
(let factlp ((count 1) (answer 1))
(if (> count n)
answer
(factlp (+ count 1) (* count answer)))))
(factorial 6)
720
Here, the symbol factlp following the let is locally defined to be a procedure that has the variables count and answer as its formal parameters. It is called the first time with the expressions 1 and 1, initializing the loop. Whenever the procedure named factlp is called later, these variables get new values that are the values of the operand expressions (+ count 1) and (* count answer).
Data can be glued together to form compound data structures. A list is a data structure in which the elements are linked sequentially. A Scheme vector is a data structure in which the elements are packed in a linear array. New elements can be added to lists, but to access the nth element of a list takes computing time proportional to n. By contrast a Scheme vector is of fixed length, and its elements can be accessed in constant time. All data structures in this book are implemented as combinations of lists and Scheme vectors. Compound data objects are constructed from components by procedures called constructors and the components are accessed by selectors.
The procedure list is the constructor for lists. The selector list-ref gets an element of the list. All selectors in Scheme are zero-based. For example,
(define a-list (list 6 946 8 356 12 620))
a-list
(6 946 8 356 12 620)
(list-ref a-list 3)
356
(list-ref a-list 0)
6
Lists are built from pairs. A pair is made using the constructor cons. The selectors for the two components of the pair are car and cdr (pronounced ``could-er'').7 A list is a chain of pairs, such that the car of each pair is the list element and the cdr of each pair is the next pair, except for the last cdr, which is a distinguishable value called the empty list and is written (). Thus,
(car a-list)
6
(cdr a-list)
(946 8 356 12 620)
(car (cdr a-list))
946
(define another-list
(cons 32 (cdr a-list)))
another-list
(32 946 8 356 12 620)
(car (cdr another-list))
946
Both a-list and another-list share the same tail (their cdr).
There is a predicate pair? that is true of pairs and false on all other types of data.
Vectors are simpler than lists. There is a constructor vector that can be used to make vectors and a selector vector-ref for accessing the elements of a vector:
(define a-vector
(vector 37 63 49 21 88 56))
a-vector
#(37 63 49 21 88 56)
(vector-ref a-vector 3)
21
(vector-ref a-vector 0)
37
Notice that a vector is distinguished from a list on printout by the character # appearing before the initial parenthesis.
There is a predicate vector? that is true of vectors and false for all other types of data.
The elements of lists and vectors may be any kind of data, including numbers, procedures, lists, and vectors. Numerous other procedures for manipulating list-structured data and vector-structured data can be found in the Scheme online documentation.
Symbols are a very important kind of primitive data type that we use to make programs and algebraic expressions. You probably have noticed that Scheme programs look just like lists. In fact, they are lists. Some of the elements of the lists that make up programs are symbols, such as + and vector. If we are to make programs that can manipulate programs, we need to be able to write an expression that names such a symbol. This is accomplished by the mechanism of quotation. The name of the symbol + is the expression '+, and in general the name of an expression is the expression preceded by a single quote character. Thus the name of the expression (+ 3 a) is '(+ 3 a).
We can test if two symbols are identical by using the predicate eq?. For example, we can write a program to determine if an expression is a sum:
(define (sum? expression)
(and (pair? expression)
(eq? (car expression) '+)))
(sum? '(+ 3 a))
#t
(sum? '(* 3 a))
#f
Here #t and #f are the printed representations of the boolean values true and false.
Consider what would happen if we were to leave out the quote in the expression (sum? '(+ 3 a)). If the variable a had the value 4 we would be asking if 7 is a sum. But what we wanted to know was whether the expression (+ 3 a) is a sum. That is why we need the quote.
1 Many of the statements here are valid only assuming that no assignments are used.
2 In examples we show the value that would be printed by the Scheme system using slanted characters following the input expression.
3 In Scheme every parenthesis is essential: you cannot add extra parentheses or remove any.
4 The logician Alonzo Church [13] invented
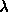 -notation to
allow the specification of an anonymous function of a named parameter:
-notation to
allow the specification of an anonymous function of a named parameter:
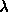 x [ expression in x].
This is read, ``That function of one argument
that is obtained by substituting the argument for x in the
indicated expression.''
x [ expression in x].
This is read, ``That function of one argument
that is obtained by substituting the argument for x in the
indicated expression.''
5 The definition of square given here is not the definition of square in the Scmutils system. In Scmutils, square is extended for tuples to mean the sum of the squares of the components of the tuple. However, for arguments that are not tuples the Scmutils square does multiply the argument by itself.
6 The examples are indented to help with readability. Scheme does not care about extra white space, so we may add as much as we please to make things easier to read.
7 These names are accidents of history. They stand for ``Contents of the Address part of Register'' and ``Contents of the Decrement part of Register'' of the IBM 704 computer, which was used for the first implementation of Lisp in the late 1950s. Scheme is a dialect of Lisp.