5.10  Lie Series

Taylor's theorem gives us a way of approximating the value of a nice enough function at a point near to a point where the value is known. If we know f and all of its derivatives at t then we can get the value of f(t + ), for small enough , as follows:

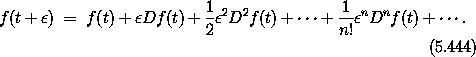
We recall that the power series for the exponential function is

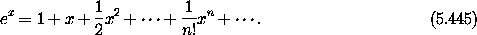
This suggests that we can formally construct a Taylor-series operator as the exponential of a differential operator³⁴

and write

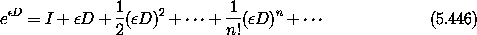
We have to be a bit careful here: ( D)² = D D. We can turn it into ² D² only because is a scalar constant, which commutes with every differential operator. But with this caveat in mind we can define the differential operator

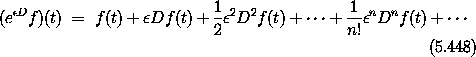
Before going on, it is interesting to compute with these a bit. In the code transcripts that follow we develop the series by exponentiation. We can examine the series incrementally by looking at successive elements of the (infinite) sequence of terms of the series. The procedure series:for-each is an incremental traverser that applies its first argument to successive elements of the series given as its second argument. The third argument (when given) specifies the number of terms to be traversed. In each of the following transcripts we print simplified expressions for the successive terms.

The first thing to look at is the general Taylor expansion for an unknown literal function, expanded around t, with increment . Understanding what we see in this simple problem will help us understand more complex problems later.

(series:for-each print-expression
 (((exp (* 'epsilon D))
   (literal-function 'f))
  't)
 6)

(f t)
(* ((D f) t) epsilon)
(* 1/2 (((expt D 2) f) t) (expt epsilon 2))
(* 1/6 (((expt D 3) f) t) (expt epsilon 3))
(* 1/24 (((expt D 4) f) t) (expt epsilon 4))
(* 1/120 (((expt D 5) f) t) (expt epsilon 5))
...

We can also look at the expansions of particular functions that we recognize, such as the expansion of sin around 0.

(series:for-each print-expression
   (((exp (* 'epsilon D)) sin) 0)
   6)

0
epsilon
0
(* -1/6 (expt epsilon 3))
0
(* 1/120 (expt epsilon 5))
...

It is often instructive to expand functions we usually don't remember, such as f(x) = (1 + x)^1/2.

(series:for-each print-expression
 (((exp (* 'epsilon D))
   (lambda (x) (sqrt (+ x 1))))
  0)
 6)

1
(* 1/2 epsilon)
(* -1/8 (expt epsilon 2))
(* 1/16 (expt epsilon 3))
(* -5/128 (expt epsilon 4))
(* 7/256 (expt epsilon 5))
...

Exercise 5.27.  Binomial series

Develop the binomial expansion of (1 + x)ⁿ as a Taylor expansion. Of course, it must be the case that for n a positive integer all of the coefficients except for the first n + 1 are zero. However, in the general case, for symbolic n, the coefficients are rather complicated polynomials in n. For example, you will find that the seventh term is

(+ (* 1/5040 (expt n 7))
   (* -1/240 (expt n 6))
   (* 5/144 (expt n 5))
   (* -7/48 (expt n 4))
   (* 29/90 (expt n 3))
   (* -7/20 (expt n 2))
   (* 1/7 n))

These terms must evaluate to the entries in Pascal's triangle. In particular, this polynomial must be zero for n<7. How is this arranged?

Dynamics

Now, to play this game with dynamical functions we want to provide a derivative-like operator that we can exponentiate, which will give us the time-advance operator. The key idea is to write the derivative of the function in terms of the Poisson bracket. Equation (3.79) shows how to do this in general:

We define the operator D_H by

so

and iterates of this operator can be used to compute higher-order derivatives:

We can express the advance of the path function f = Fo for an interval with respect to H as a power series in the derivative operator D_H applied to the phase-space function F and then composed with the path:

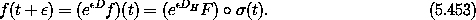
Indeed, we can implement the time-advance operator with this series when it converges.

Exercise 5.28.  Iterated derivatives
Show that equation (5.452) is correct.

Exercise 5.29.  Lagrangian analog
Compare D_H with the total time derivative operator. Recall that

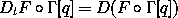
abstracts the derivative of a function of a path through state space to a function of the derivatives of the path. Define another derivative operator D_L, analogous to D_H, that would give the time derivative of functions along Lagrangian state paths that are solutions of Lagrange's equations for a given Lagrangian. How might this be useful?

For time-independent Hamiltonian H and time-independent state function F, we can simplify the computation of the advance of F. In this case we define the Lie derivative operator L_H such that

which reads ``the Lie derivative of F with respect to H.''³⁵ So

and for time-independent F

We can iterate this process to compute higher derivatives. So

and successively higher-order Poisson brackets of F with H give successively higher-order derivatives when evaluated on the trajectory.

Let f = F o . We have

Thus we can rewrite the advance of the path function f for an interval with respect to H as a power series in the Lie derivative operator applied to the phase-space function F and then composed with the path:

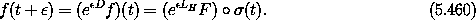
We can implement the time-advance operator E'_,H with the Lie series e ^L_H F when this series converges:

We have shown that time evolution is canonical, so the series above are formal representations of canonical transformations as power series in the time. These series may not converge, even if the evolution governed by the Hamiltonian H is well defined.

Computing Lie series

We can use the Lie transform as a computational tool to examine the local evolution of dynamical systems. We define the Lie derivative of F as a derivative-like operator relative to the given Hamiltonian function, H:³⁶

(define ((Lie-derivative H) F)
  (Poisson-bracket F H))

We also define a procedure to implement the Lie transform:³⁷

(define (Lie-transform H t)
  (exp (* t (Lie-derivative H))))

Let's start by examining the beginning of the Lie series for the position of a simple harmonic oscillator of mass m and spring constant k. We can implement the Hamiltonian as

(define ((H-harmonic m k) state)
  (+ (/ (square (momentum state)) (* 2 m))
     (* 1/2 k (square (coordinate state)))))

We make the Lie transform (series) by passing the Lie-transform operator an appropriate Hamiltonian function and an interval to evolve for. The resulting operator is then given the coordinate procedure, which selects the position coordinates from the phase-space state. The Lie transform operator returns a procedure that, when given a phase-space state composed of a dummy time, a position x0, and a momentum p0, returns the position resulting from advancing that state by the interval dt.

(series:for-each print-expression
 (((Lie-transform (H-harmonic 'm 'k) 'dt)
   coordinate)
  (up 0 'x0 'p0))
 6)

x0
(/ (* dt p0) m)
(/ (* -1/2 (expt dt 2) k x0) m)
(/ (* -1/6 (expt dt 3) k p0) (expt m 2))
(/ (* 1/24 (expt dt 4) (expt k 2) x0) (expt m 2))
(/ (* 1/120 (expt dt 5) (expt k 2) p0) (expt m 3))
...

We should recognize the terms of this series. We start with the initial position x₀. The first-order correction (p₀/m) dt is due to the initial velocity. Next we find an acceleration term ( - k x₀/2m) dt² due to the restoring force of the spring at the initial position.

The Lie transform is just as appropriate for showing us how the momentum evolves over the interval:

(series:for-each print-expression
 (((Lie-transform (H-harmonic 'm 'k) 'dt)
   momentum)
  (up 0 'x0 'p0))
 6)

p0
(* -1 dt k x0)
(/ (* -1/2 (expt dt 2) k p0) m)
(/ (* 1/6 (expt dt 3) (expt k 2) x0) m)
(/ (* 1/24 (expt dt 4) (expt k 2) p0) (expt m 2))
(/ (* -1/120 (expt dt 5) (expt k 3) x0) (expt m 2))
...

In this series we see how the initial momentum p₀ is corrected by the effect of the restoring force - k x₀ dt, etc.

What is a bit more fun is to see how a more complex phase-space function is treated by the Lie series expansion. In the experiment below we examine the Lie series developed by advancing the harmonic-oscillator Hamiltonian, by means of the transform generated by the same harmonic-oscillator Hamiltonian:

(series:for-each print-expression
 (((Lie-transform (H-harmonic 'm 'k) 'dt)
   (H-harmonic 'm 'k))
  (up 0 'x0 'p0))
 6)

(/ (+ (* 1/2 k m (expt x0 2)) (* 1/2 (expt p0 2))) m)
0
0
0
0
0
...

As we would hope, the series shows us the original energy expression (k/2)x₀² + (1/2m)p₀² as the first term. Each subsequent correction term turns out to be zero -- because the energy is conserved.

Of course, the Lie series can be used in much more complex situations where we want to see the expansion of the motion of a system characterized by a more complex Hamiltonian. The planar motion of a particle in a general central field (see equation 3.99) is a simple problem for which the Lie series is instructive. In the following transcript we can see how rapidly the series becomes complicated. It is worth one's while to try to interpret the additive parts of the third (acceleration) term shown below:

(series:for-each print-expression
 (((Lie-transform
    (H-central-polar 'm (literal-function 'U))
    'dt)
   coordinate)
  (up 0
      (up 'r_0 'phi_0)
      (down 'p_r_0 'p_phi_0)))
 4)
(up r_0 phi_0)
(up (/ (* dt p_r_0) m)
    (/ (* dt p_phi_0) (* m (expt r_0 2))))
(up
 (+ (/ (* -1/2 ((D U) r_0) (expt dt 2)) m)
    (/ (* 1/2 (expt dt 2) (expt p_phi_0 2))
       (* (expt m 2) (expt r_0 3))))
 (/ (* -1 (expt dt 2) p_phi_0 p_r_0)
    (* (expt m 2) (expt r_0 3))))
(up
 (+ (/ (* -1/6 (((expt D 2) U) r_0) (expt dt 3) p_r_0)
       (expt m 2))
    (/ (* -1/2 (expt dt 3) (expt p_phi_0 2) p_r_0)
       (* (expt m 3) (expt r_0 4))))
 (+ (/ (* 1/3 ((D U) r_0) (expt dt 3) p_phi_0)
       (* (expt m 2) (expt r_0 3)))
    (/ (* -1/3 (expt dt 3) (expt p_phi_0 3))
       (* (expt m 3) (expt r_0 6)))
    (/ (* (expt dt 3) p_phi_0 (expt p_r_0 2))
       (* (expt m 3) (expt r_0 4)))))
...

Of course, if we know the closed-form Lie transform it is probably a good idea to take advantage of it, but when we do not know the closed form the Lie series representation of it can come in handy.