 governed by H is a canonical transformation
governed by H is a canonical transformation 
 , H. Evolution by W for an interval
, H. Evolution by W for an interval  is a
canonical transformation
is a
canonical transformation  '
' , W:
, W:
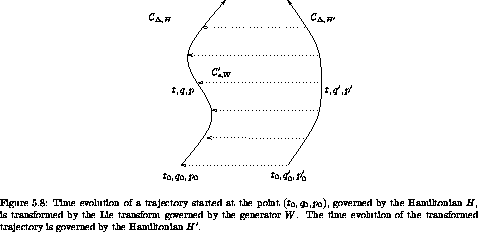
The evolution of a system under any Hamiltonian generates a continuous family of canonical transformations. To study the behavior of some system governed by a Hamiltonian H, it is sometimes appropriate to use a canonical transformation generated by evolution governed by another Hamiltonian-like function W on the same phase space. Such a canonical transformation is called a Lie transform.
The functions H and W are both Hamiltonian-shaped functions
defined on the same phase space. Time evolution for an interval
 governed by H is a canonical transformation
governed by H is a canonical transformation 
 , H. Evolution by W for an interval
, H. Evolution by W for an interval  is a
canonical transformation
is a
canonical transformation  '
' , W:
, W:

The independent
variable in the H evolution is time, and the independent variable in
the W evolution is an arbitrary parameter of the canonical
transformation. We chose  ' for the W evolution so that
the canonical transformation induced by W does not change the time
in the system governed by H.
' for the W evolution so that
the canonical transformation induced by W does not change the time
in the system governed by H.
Figure 5.9 shows how a Lie transform is used to transform a trajectory. We can see from the diagram that the canonical transformations obey the relation

For generators W that do not depend on the independent variable, the
resulting canonical transformation  '
' , W is
time independent and symplectic. A time-independent symplectic
transformation is canonical if the Hamiltonian
transforms by composition:32
, W is
time independent and symplectic. A time-independent symplectic
transformation is canonical if the Hamiltonian
transforms by composition:32

We will use only Lie transforms that have generators that do not depend on the independent variable.
The value of a phase-space function F changes if its arguments
change. We define the function E' , W of a
function F of phase-space coordinates (t, q, p) by
, W of a
function F of phase-space coordinates (t, q, p) by

We say that E' , W F is the Lie transform of the function F.
, W F is the Lie transform of the function F.
In particular, the Lie transform advances the coordinate and momentum selector functions Q = I1 and P = I2:
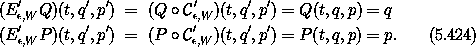
So we may restate equation (5.422) as
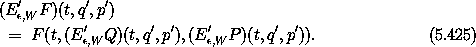
More generally, Lie transforms descend into compositions:

In terms of E' , W we have the canonical transformation
, W we have the canonical transformation


where I is the phase-space identity function: I(t, q, p) = (t, q, p).
Note that E' , W has the property:33
, W has the property:33
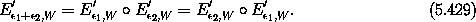

We can define the inverse function

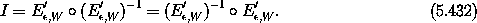
For example, suppose we are studying a system for which a rotation would be a helpful transformation. To concoct such a transformation we note that we intend a configuration coordinate to increase uniformly with a given rate. In this case we want an angle to be incremented. The Hamiltonian that consists solely of the momentum conjugate to that configuration coordinate always does the job. So the angular momentum is an appropriate generator for rotations.
The analysis is simple if we use polar coordinates r,  with
conjugate momenta pr, p
with
conjugate momenta pr, p . The generator W is just:
. The generator W is just:

The family of transformations satisfies Hamilton's equations:

The only variable that appears in W is p , so
, so
 is the only variable that varies as
is the only variable that varies as  is varied. In
fact, the family of canonical transformations is
is varied. In
fact, the family of canonical transformations is

So angular momentum is the generator of a canonical rotation.
The example is simple, but it illustrates one important feature of Lie transformations -- they give one set of variables entirely in terms of the other set of variables. This should be contrasted with the mixed-variable generating function transformations, which always give a mixture of old and new variables in terms of a mixture of new and old variables, and thus require an inversion to get one set of variables in terms of the other set of variables. This inverse can be written in closed form only for special cases. In general, there is considerable advantage in using a transformation rule that generates explicit transformations from the start. The Lie transformations are always explicit in the sense that they give one set of variables in terms of the other, but for there to be explicit expressions the evolution governed by the generator must be solvable.
Let's consider another example. This time consider a three-degree-of-freedom problem in rectangular coordinates, and take the generator of the transformation to be the z component of the angular momentum:
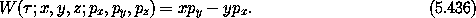

We notice that z and pz are unchanged, and that the equations governing the evolution of x and y decouple from those of px and py. Each of these pairs of equations represents simple harmonic motion, as can be seen by writing them as second-order systems. The solutions are

So we see that again a component of the angular momentum generates a canonical rotation. There was nothing special about our choice of axes, so we can deduce that the component of angular momentum about any axis generates rotations about that axis.
Suppose we have a system governed by the Hamiltonian
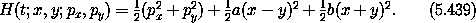
Hamilton's equations couple the motion of x and y:
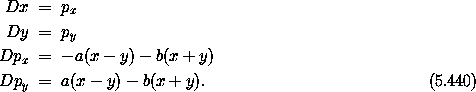
We can decouple the system by performing a coordinate rotation by
 /4. This is generated by
/4. This is generated by

which is similar to the generator for the coordinate rotation above but without the z degree of
freedom. Evolving ( ; x, y; px, py) by W for an interval of
; x, y; px, py) by W for an interval of  /4 gives
a canonical rotation:
/4 gives
a canonical rotation:
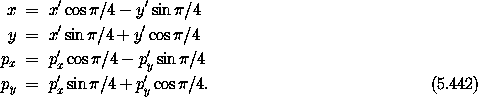
Composing the Hamiltonian H with this time-independent transformation gives the new Hamiltonian
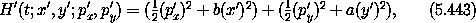
which is a Hamiltonian for two uncoupled harmonic oscillators. So the original coupled problem has been transformed by a Lie transform to a new form for which the solution is easy.
32 In general, the generator W could depend on its
independent variable. If so, it would be necessary to specify a rule
that gives the initial value of the independent variable for the W
evolution. This rule may or may not depend upon the time. If the
specification of the independent variable for the W evolution does
not depend on time, then the resulting canonical transformation  '
' , W is time independent and the Hamiltonians transform
by composition. If the generator W depends on its independent
variable and the rule for specifying its initial value depends on
time, then the transformation
, W is time independent and the Hamiltonians transform
by composition. If the generator W depends on its independent
variable and the rule for specifying its initial value depends on
time, then the transformation  '
' , W is time
dependent. In this case there may need to be an adjustment to the
relation between the Hamiltonians H and H'. In the extended phase
space all these complications disappear. There is only one case. We
can assume all generators W are independent of the independent
variable.
, W is time
dependent. In this case there may need to be an adjustment to the
relation between the Hamiltonians H and H'. In the extended phase
space all these complications disappear. There is only one case. We
can assume all generators W are independent of the independent
variable.
33 The set of transformations E' , W with the operation
composition and with parameter
, W with the operation
composition and with parameter  is a one-parameter Lie
group.
is a one-parameter Lie
group.