
Other problems are encountered in applying perturbation theory to systems with more than a single degree of freedom. Consider a Hamiltonian of the form

where H0 depends only on the momenta and so is solvable. We assume that the Hamiltonian has no explicit time dependence. We further assume that the coordinates are all angles and that H1 is a multiply periodic function of the coordinates.
Carrying out a Lie transformation with generator W produces the Hamiltonian
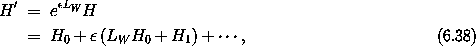
as before. The condition that the order- terms are
eliminated is
terms are
eliminated is

a linear partial differential equation. By assumption, the Hamiltonian H0 depends only on the momenta. We define

the tuple of frequencies of the unperturbed system. The condition on W is

As H1 is a multiply-periodic function of the coordinates, we can write it as a Poisson series:1

Similarly, we assume W can be written as a Poisson series:

Substituting these into the condition that order- terms are eliminated, we find
terms are eliminated, we find
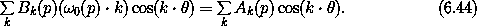
The cosines are orthogonal so each term must be individually zero. We deduce

and that the required Lie generator is
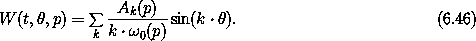
There are a couple of problems. First, if A0 is nonzero
then the expression for B0 involves a division by zero. So the
expression for B0 is not correct. The problem is that the
corresponding term in H1 does not involve  . So the
integration for B0 should introduce linear terms in
. So the
integration for B0 should introduce linear terms in  . But
this is the same situation that led to the secular terms in the
perturbation approximation to the pendulum. Having learned our lesson
there, we avoid the secular terms by adjoining this term to the
solvable Hamiltonian and excluding k = 0 from the sum for W.
We have
. But
this is the same situation that led to the secular terms in the
perturbation approximation to the pendulum. Having learned our lesson
there, we avoid the secular terms by adjoining this term to the
solvable Hamiltonian and excluding k = 0 from the sum for W.
We have

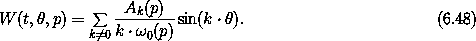
Another problem is that there are many opportunities for small
denominators that would make the perturbation large and therefore
not a perturbation. As we saw in the perturbation approximation for
the pendulum in terms of the rotor, we must exclude certain regions
from the domain of applicability of the perturbation approximation.
These excluded regions are associated with commensurabilities among
the frequencies  0(p).
Consider the phase-space transformation of the coordinates
0(p).
Consider the phase-space transformation of the coordinates
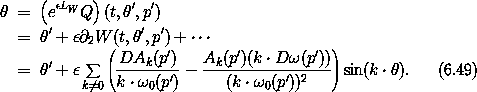
So we must exclude from the domain of applicability all regions for which the coefficients are large. If the second term dominates, the excluded regions satisfy
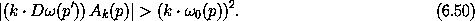
Considering the fact that for any tuple of frequencies  0(p') we can find a
tuple of integers k such that k ·
0(p') we can find a
tuple of integers k such that k ·  (p') is arbitrarily
small, this problem of small divisors looks very serious.
(p') is arbitrarily
small, this problem of small divisors looks very serious.
However, the problem, though serious, is not as bad as it may appear, for a couple of reasons. First, it may be that Ak ne 0 only for certain k. In this case, only the regions for these terms are excluded from the domain of applicability. Second, for analytic functions the magnitude of Ak decreases strongly with the size of k (see [4]):

for some positive ß and C, and where | k |+ = | k0 | + | k1 | + ··· . At any stage of a perturbation approximation we can limit consideration to just those terms that are larger than a specified magnitude. The size of the excluded region corresponding to a term is of order square root of |Ak(p')| and the inequality (6.51) shows that |Ak(p')| decreases exponentially with the order of the term.
More concretely, consider the periodically driven pendulum. We will develop approximate solutions for the driven pendulum as a perturbed rotor.
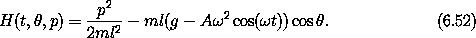
We can remove the explicit time dependence by going to the extended phase space. The Hamiltonian is
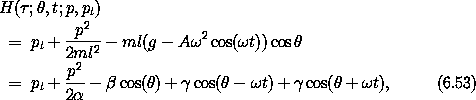
with the constants  = ml2, ß = mlg, and
= ml2, ß = mlg, and  = (1/2) m l
A
= (1/2) m l
A  2 .
2 .
With the intent to approximate the driven pendulum as a perturbed rotor, we choose
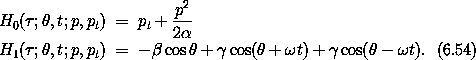
Notice that the perturbation H1 has only three terms in its Poisson series, so in the first perturbation step only three regions will be excluded from the domain of applicability. The perturbation H1 is particularly simple: it has only three terms, and the coefficients are constants.
The Lie series generator that eliminates the terms in H1 to first
order in  , satisfying
, satisfying

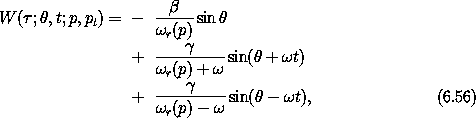
where  r(p) =
r(p) =  2,0 H0(
2,0 H0( ;
;  , t; p, pt) = p/
, t; p, pt) = p/ is the unperturbed rotor frequency.
is the unperturbed rotor frequency.
The resulting approximate solution has three regions in which there
are small denominators, and so three regions that are excluded from
applicability of the perturbative solution. Regions of phase space
for which  r(p) is near 0,
r(p) is near 0,  , and -
, and -  are
excluded. Away from these regions
the perturbative solution works well, just as in the rotor
approximation for the pendulum. Unfortunately, some of the more
interesting regions of the phase space of the driven pendulum are
excluded: the region in which we find the remnant of the undriven
pendulum is excluded, as are the two resonance regions in which the
rotation of the pendulum is synchronous with the drive. We need to
develop methods for approximating these regions.
are
excluded. Away from these regions
the perturbative solution works well, just as in the rotor
approximation for the pendulum. Unfortunately, some of the more
interesting regions of the phase space of the driven pendulum are
excluded: the region in which we find the remnant of the undriven
pendulum is excluded, as are the two resonance regions in which the
rotation of the pendulum is synchronous with the drive. We need to
develop methods for approximating these regions.
1 In general, we need to include sine terms as well, but the cosine expansion is enough for this illustration.