
The pendulum is a simple one-degree-of-freedom system, for which the solutions are known. If we consider the pendulum as a free rotor with the added complication of gravity, then we can carry out a perturbation step as just described to see how well it approximates the known motion of the pendulum.
The motion of a pendulum is described by the Hamiltonian

with coordinate  and conjugate angular momentum p, where
and conjugate angular momentum p, where
 = ml2 and ß = mgl. The parameter
= ml2 and ß = mgl. The parameter  allows us to
scale the perturbation; it is 1 for the actual pendulum.
We divide the Hamiltonian into the free-rotor Hamiltonian and the
perturbation from gravity:
allows us to
scale the perturbation; it is 1 for the actual pendulum.
We divide the Hamiltonian into the free-rotor Hamiltonian and the
perturbation from gravity:


The Lie generator W satisfies condition (6.7):



where the arbitrary integration constant is ignored.
The transformed Hamiltonian is H' = H0 + o( 2). If we can
ignore the
2). If we can
ignore the  2 contributions, then the transformed
Hamiltonian is simply
2 contributions, then the transformed
Hamiltonian is simply


To connect these solutions to the solutions of the original problem, we use the Lie series
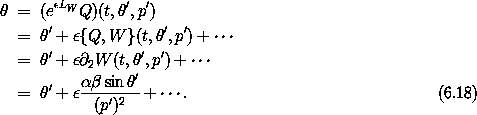

Note that if the Lie series is truncated it is not exactly a canonical transformation; only the infinite series is canonical.
The initial values  '0 and p'0 are determined from the
initial values of
'0 and p'0 are determined from the
initial values of  and p by the inverse Lie transformation:
and p by the inverse Lie transformation:


Note that if we truncate the coordinate transformations after the
first-order terms in  (or any finite order), then the inverse
transformation is not exactly the inverse of the transformation.
(or any finite order), then the inverse
transformation is not exactly the inverse of the transformation.
The approximate solution for given initial conditions (t0,  0,
p0) is obtained by finding the corresponding (t0,
0,
p0) is obtained by finding the corresponding (t0,  '0,
p'0) using the transformation (6.20)
and (6.21). Then the system is evolved
using the solutions (6.17). The phase-space
coordinates of the evolved point are transformed back to the original
variables using the
transformation (6.18) and
(6.19).
'0,
p'0) using the transformation (6.20)
and (6.21). Then the system is evolved
using the solutions (6.17). The phase-space
coordinates of the evolved point are transformed back to the original
variables using the
transformation (6.18) and
(6.19).
We define the two parts of the pendulum Hamiltonian:
(define ((H0 alpha) state)
(let ((p (momentum state)))
(/ (square p) (* 2 alpha))))
(define ((H1 beta) state)
(let ((theta (coordinate state)))
(* -1 beta (cos theta))))
The Hamiltonian for the pendulum can be expressed as a series
expansion in the parameter  by
by
(define (H-pendulum-series alpha beta epsilon)
(series (H0 alpha) (* epsilon (H1 beta))))
where the series procedure is a constructor for a series whose
first terms are given and all further terms are zero.
The Lie generator that eliminates the order- terms is
terms is
(define ((W alpha beta) state)
(let ((theta (coordinate state))
(p (momentum state)))
(/ (* -1 alpha beta (sin theta)) p)))
We check that W satisfies condition (6.7):
(print-expression
((+ ((Lie-derivative (W 'alpha 'beta)) (H0 'alpha))
(H1 'beta))
(up 't 'theta 'p)))
0
and that it has the desired effect on the Hamiltonian:
(show-expression
(series:sum
(((exp (* 'epsilon (Lie-derivative (W 'alpha 'beta))))
(H-pendulum-series 'alpha 'beta 'epsilon))
(up 't 'theta 'p))
2))
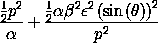
Indeed, the order- term has been removed and an
order-
term has been removed and an
order- 2 term has been introduced.
2 term has been introduced.
Ignoring the  2 terms in the new Hamiltonian, the solution is
2 terms in the new Hamiltonian, the solution is
(define (((solution0 alpha beta) t) state0)
(let ((t0 (time state0))
(theta0 (coordinate state0))
(p0 (momentum state0)))
(up t
(+ theta0 (/ (* (- t t0) p0) alpha))
p0)))
The transformation from primed to unprimed phase-space coordinates is, including terms up to order,
(define ((C alpha beta epsilon order) state)
(series:sum
(((Lie-transform (W alpha beta) epsilon)
identity)
state)
order))
To second order in  the transformation generated by W is
the transformation generated by W is
(show-expression
((C 'alpha 'beta 'epsilon 2) (up 't 'theta 'p)))
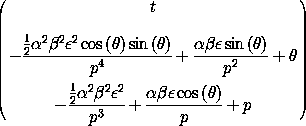
The inverse transformation is
(define (C-inv alpha beta epsilon order)
(C alpha beta (- epsilon) order))
With these components, the perturbative solution (equation 6.9) is
(define (((solution epsilon order) alpha beta) delta-t)
(compose (C alpha beta epsilon order)
((solution0 alpha beta) delta-t)
(C-inv alpha beta epsilon order)))
The resulting procedure maps an initial state to the solution state advanced by delta-t.
We can examine the behavior of the perturbative solution and compare it to the true behavior of the pendulum. There are several considerations. We have truncated the Lie series for the phase-space transformation. Does the missing part matter? If the missing part does not matter, how well does this perturbation step work?
Figure 6.1 shows that as we increase the
number of terms in the Lie series for the phase-space coordinate
transformation the result appears to converge. The lone trajectory
includes only terms of first order. The others, including terms of
second, third, and fourth order, are closely clustered. On the left
edge of the graph (at  = -
= -  ), the order of the solution
increases from the top to the bottom of the graph. In the middle (at
), the order of the solution
increases from the top to the bottom of the graph. In the middle (at
 = 0), the fourth-order curve is between the second-order curve
and the third-order curve. In addition to the error in phase-space
path, there is also an error in the period -- the higher-order orbits
have longer periods than the first-order orbit. The parameters are
= 0), the fourth-order curve is between the second-order curve
and the third-order curve. In addition to the error in phase-space
path, there is also an error in the period -- the higher-order orbits
have longer periods than the first-order orbit. The parameters are
 = 1.0 and ß = 0.1. We have set
= 1.0 and ß = 0.1. We have set  = 1. Each
trajectory was started at
= 1. Each
trajectory was started at  = 0 with p = 0.7. Notice that
the initial point on the solution varies between trajectories. This
is because the transformation is not perfectly inverted by the
truncated Lie series.
= 0 with p = 0.7. Notice that
the initial point on the solution varies between trajectories. This
is because the transformation is not perfectly inverted by the
truncated Lie series.
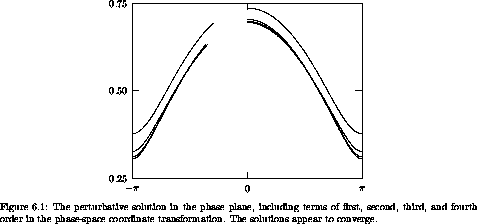
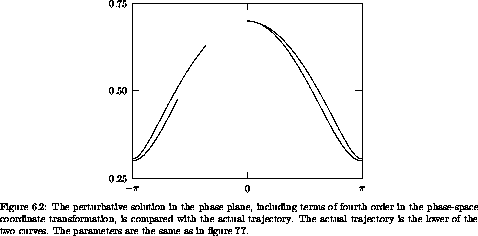
Figure 6.2 compares the perturbative solution (with terms up to fourth order) with the actual trajectory of the pendulum. The initial points coincide, to the precision of the graph, because the terms to fourth order are sufficient. The trajectories deviate both in the phase plane and in the period, but they are still quite close.
The trajectories of figures 6.1 and
6.2 are all for the same initial state. As we
vary the initial state we find that for trajectories in the
circulation region, far from the separatrix, the perturbative solution
does quite well. However, if we get close to the separatrix or if we
enter the oscillation region, the perturbative solution is nothing like
the real solution, and it does not even seem to converge.
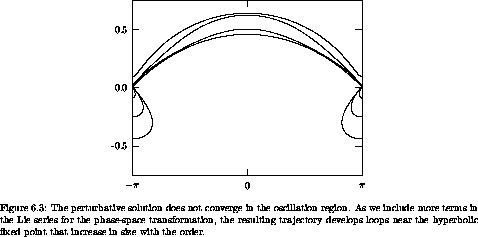
Figure 6.3 shows what happens when we try to use
the perturbative solution inside the oscillation region.
Each trajectory was started at  = 0 with p = 0.55. The
parameters are
= 0 with p = 0.55. The
parameters are  = 1.0 and ß = 0.1.
= 1.0 and ß = 0.1.
This failure of the perturbation solution should not be surprising. We assumed that the real motion was a distorted version of the motion of the free rotor. But in the oscillation region the assumption is not true -- the pendulum is not rotating at all. The perturbative solutions can be valid (if they work at all!) only in a region where the topology of the real orbits is the same as the topology of the perturbative solutions.
We can make a crude estimate of the range of validity of the perturbative
solution by looking at the first correction term in the phase-space
transformation (6.18). The correction
in  is proportional to
is proportional to 
 ß / (p')2. This is
not a small perturbation if
ß / (p')2. This is
not a small perturbation if

This sets the scale for the validity of the perturbative solution.
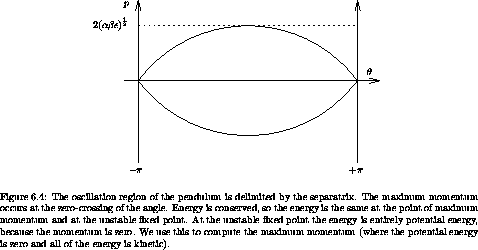
We can compare this scale to the size of the oscillation region (see
figure 6.4). We can obtain the width of
the region of oscillation of the pendulum by considering the
separatrix. The value of the Hamiltonian on the separatrix is the
same as the value at the unstable equilibrium: H(t,  =
=  ,
p = 0) = ß
,
p = 0) = ß  . The separatrix has maximum momentum
psep at
. The separatrix has maximum momentum
psep at  = 0:
= 0:

Solving for psep, the half-width of the region of oscillation, we find

Comparing equations (6.22) and (6.24), we see that the requirement that the terms in the perturbation solution be small excludes a region of the phase space with the same scale as the region of oscillation of the pendulum.
What the perturbation theory is doing is deforming the phase-space coordinate system so that the problem looks like the free-rotor problem. This deformation is sensible only in the circulating case. So, it is not surprising that the perturbation theory fails in the oscillation region. What may be surprising is how well the perturbation theory works just outside the oscillation region. The range of p in which the perturbation theory is not valid scales in the same way as the width of the oscillation region. This need not have been the case -- the perturbation theory could have failed over a wider range.
Exercise 6.1. Symplectic residual
For the transformation
(C alpha beta epsilon order),
compute the residuals in the symplectic test for various orders of
truncation of the Lie series.
We can improve the perturbative solution by carrying out additional perturbation steps. The overall plan is the same as before. We perform a Lie transformation with a new generator that eliminates the desired terms from the Hamiltonian.
After the first step the
Hamiltonian is, to second order in  ,
,
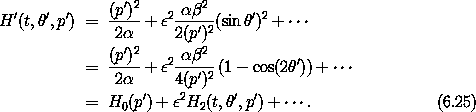
Performing a Lie transformation with generator W' yields the Hamiltonian
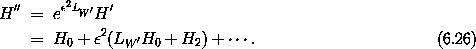
So the condition on W' that the second-order terms are eliminated is

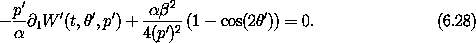
A generator that satisfies this condition is
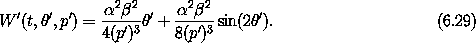
There are two contributions to this generator, one proportional to
 ' and the other involving a trigonometric function of
' and the other involving a trigonometric function of
 '.
'.
The phase-space coordinate transformation resulting from this Lie transform is found as before. For given initial conditions, we first carry out the inverse transformation corresponding to W, then that for W', solve for the evolution of the system using H0, then transform back using W' and then W. The approximate solution is
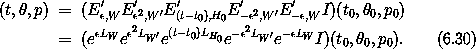
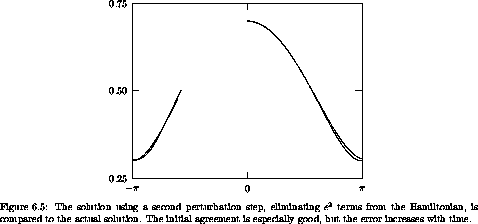
The solution obtained in this way is
compared to the actual evolution of the pendulum in
figure 6.5. Terms in all Lie series up to  4 are included. The perturbative solution,
including this second perturbative step, is much closer to the actual
solution in the initial segment than the first-order perturbative
solution (figure 6.2).
The time interval spanned is 10.
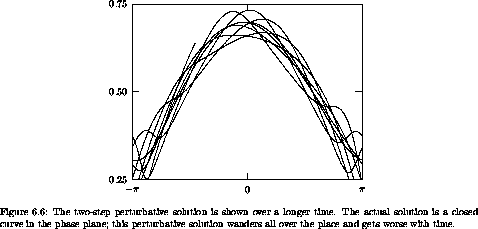
Over longer times the second-order perturbative solution diverges dramatically from the actual
solution, as
shown in figure 6.6.
These solutions begin at
4 are included. The perturbative solution,
including this second perturbative step, is much closer to the actual
solution in the initial segment than the first-order perturbative
solution (figure 6.2).
The time interval spanned is 10.
Over longer times the second-order perturbative solution diverges dramatically from the actual
solution, as
shown in figure 6.6.
These solutions begin at
 = 0 with p = 0.7.
The parameters are
= 0 with p = 0.7.
The parameters are  = 1.0 and
ß = 0.1. The time interval
spanned is 100.
= 1.0 and
ß = 0.1. The time interval
spanned is 100.
A problem with the perturbative solution is that there are terms
in W' and in the corresponding phase-space coordinate transformation
that are proportional to  ', and
', and  ' grows linearly with
time. So the solution can be valid only for small times; the interval
of validity depends on the frequency of the particular trajectory
under investigation and the size of the coefficients multiplying the
various terms. Such terms in a perturbative representation of the
solution that are proportional to time are called secular terms.
They limit the validity of the perturbation theory to small times.
' grows linearly with
time. So the solution can be valid only for small times; the interval
of validity depends on the frequency of the particular trajectory
under investigation and the size of the coefficients multiplying the
various terms. Such terms in a perturbative representation of the
solution that are proportional to time are called secular terms.
They limit the validity of the perturbation theory to small times.
A solution to the problem of secular terms was developed
by Lindstedt and Poincaré. The goal of each perturbation step is to
eliminate terms in the Hamiltonian that prevent solution. However,
the term in H' that led to the secular term in the generator W'
does not actually impede solution. So a better procedure is to
leave that term in the Hamiltonian and find the generator W'' that
eliminates only the term that is periodic in  '.
So W'' must satisfy
'.
So W'' must satisfy
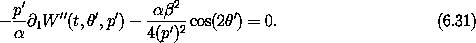

After we perform a Lie transformation with this generator, the new Hamiltonian is
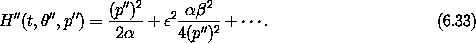
Including terms up to the  2 term, the solution is
2 term, the solution is
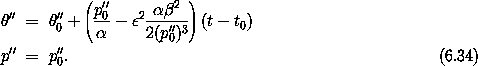
We construct the solution for a given initial condition as before by composing the transformations, the solution of the modified Hamiltonian, and the inverse transformations. The approximate solution is
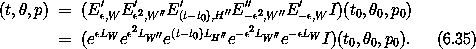
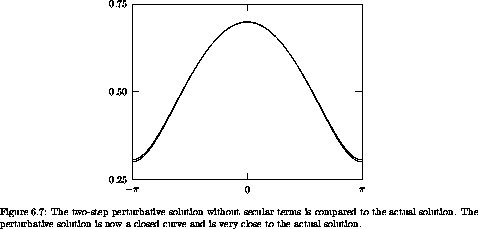
The resulting phase space evolution is shown in figure 6.7. Now the perturbative solution is a closed curve in the phase plane and is in pretty good agreement with the actual solution.
By modifying the solvable part of the Hamiltonian we are modifying the frequency of the solution. The secular terms appeared because we were trying to approximate a solution with one frequency as a Fourier series with the wrong frequency. As an analogy, consider
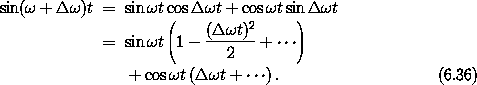
The periodic terms are multiplied by terms that are polynomials in the time. These polynomials are the initial segment of the power series for periodic functions. The infinite series are convergent, but if the series are truncated the error is large at large times.
Continuing the perturbative solution to higher orders is now a straightforward repetition of the steps carried out so far. At each step in the perturbation solution there will be new contributions to the solvable part of the Hamiltonian that absorb potential secular terms. The contribution is just the angle-independent part of the Hamiltonian after the Hamiltonian is written as a Fourier series. The constant part of the Fourier series is the same as the average of the Hamiltonian over the angle. So at each step in the perturbation theory, the average of the perturbation is included with the solvable part of the Hamiltonian and the periodic part is eliminated by a Lie transformation.