6.1  Perturbation Theory with Lie Series

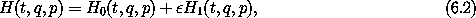
Given a system, we look for a decomposition of the Hamiltonian in the form

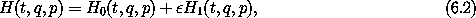
where H₀ is solvable. We assume that the Hamiltonian has no explicit time dependence; this can be ensured by going to the extended phase space if necessary. We also assume that a canonical transformation has been made so that H₀ depends solely on the momenta:

We carry out a Lie transformation and find the conditions that the Lie generator W must satisfy to eliminate the order- terms from the Hamiltonian.

The Lie transform and associated Lie series specify a canonical transformation:

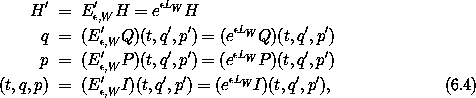
where Q = I₁ and P = I₂ are the coordinate and momentum selectors and I is the identity function. Recall the definitions

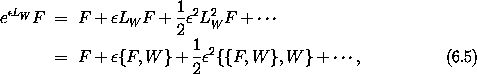
with L_W F = { F, W }.

Applying the Lie transformation to H gives us

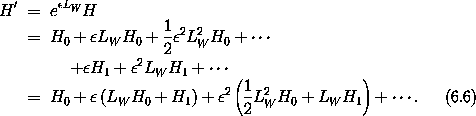
The first-order term in is zero if W satisfies the condition

which is a linear partial differential equation for W. The transformed Hamiltonian is

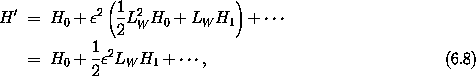
where we have used condition (6.7) to simplify the ² contribution.

This basic step of perturbation theory has eliminated terms of a certain order (order ) from the Hamiltonian, but in doing so has generated new terms of higher order (here ² and higher).

At this point we can find an approximate solution by truncating Hamiltonian (6.8) to H₀, which is solvable. The approximate solution for given initial conditions (t₀, q₀, p₀) is obtained by finding the corresponding (t₀, q'₀, p'₀) using the inverse of transformation (6.4). Then the system is evolved to time t using the solutions of the truncated Hamiltonian H₀, giving the state (t, q', p'). The phase-space coordinates of the evolved point are transformed back to the original variables using the transformation (6.4) to state (t, q, p). The approximate solution is

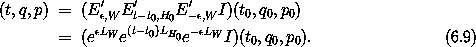
If the Lie transform E'_{, W} = e ^L_W must be evaluated by summing the series, then we must specify the order to which the sum extends.

Assuming everything goes okay, we can imagine repeating this process to eliminate the order-² terms and so on, bringing the transformed Hamiltonian as close as we like to H₀. Unfortunately, there are complications. We can understand some of these complications and how to deal with them by considering some specific applications.