Islands appear near commensurabilities, and commensurabilities are
present even in integrable systems. In integrable systems an infinite
number of periodic orbits are associated with each commensurability,
but upon perturbation only a finite number of periodic orbits survive.
How does this happen? First we have to learn more about integrable
systems.
If an n-degree-of-freedom system has n independent conserved
quantities then the solution of the problem can be reduced to
quadratures. Such a system is called integrable. Typically,
the phase space of integrable systems is divided into regions of
qualitatively different behavior. For example, the motion of a
pendulum is reducible to quadratures and has three distinct types of
solutions: the oscillating solutions and the clockwise and
counterclockwise circulating solutions. The different regions of the
pendulum phase space are separated by the trajectories that are
asymptotic to the unstable equilibrium. It turns out that for any
system that is reducible to quadratures, a set of phase-space
coordinates can be chosen for each region of the phase space so that
the Hamiltonian describing the motion in that region depends only on
the momenta. Furthermore, if the phase space is bounded then the
generalized coordinates can be chosen to be angles (that are
2 -periodic). The configuration space described by n angles is an
n-torus. The momenta conjugate to these angles are called actions. Such phase-space coordinates are called action-angle
coordinates. We will see later how to reformulate systems in this
way.
Here we explore the consequences of such a formulation; this
formulation is especially useful for finding out what happens as
additional effects are added to integrable problems.
-periodic). The configuration space described by n angles is an
n-torus. The momenta conjugate to these angles are called actions. Such phase-space coordinates are called action-angle
coordinates. We will see later how to reformulate systems in this
way.
Here we explore the consequences of such a formulation; this
formulation is especially useful for finding out what happens as
additional effects are added to integrable problems.
Suppose we have a time-independent n-degree-of-freedom system
that is reducible to quadratures. For each region of phase space
there is a local formulation of the system so that the evolution of
the system is described by a time-independent Hamiltonian that depends
only on the momenta. Suppose further that the coordinates are all
angles. Let  be the tuple of angles and J be the tuple of
conjugate momenta. The Hamiltonian is
be the tuple of angles and J be the tuple of
conjugate momenta. The Hamiltonian is
Hamilton's equations are simply
where  (J) = D f(J) is a tuple of frequencies with a
component for each degree of freedom. The momenta are all constant
because the Hamiltonian does not depend on any of the coordinates. The motion
of the coordinate angles is uniform; the rates of change of the angles
are the frequencies
(J) = D f(J) is a tuple of frequencies with a
component for each degree of freedom. The momenta are all constant
because the Hamiltonian does not depend on any of the coordinates. The motion
of the coordinate angles is uniform; the rates of change of the angles
are the frequencies  , which depend only on the constant
momenta. Given initial values
, which depend only on the constant
momenta. Given initial values  (t0) and J(t0) at time
t0, the solutions are simple:
(t0) and J(t0) at time
t0, the solutions are simple:
Though the solutions are simple, there are a number of distinct orbit
types: equilibrium solutions, periodic orbits, and quasiperiodic
orbits, depending on the frequency ratios.
If  (J) is zero for some J then
(J) is zero for some J then  and J are both
constant, for any
and J are both
constant, for any  . The system is at an equilibrium point.
. The system is at an equilibrium point.
A solution is periodic if all the coordinates (and momenta) of the
system return to their initial values at some later
time. Each coordinate  i with nonzero frequency
i with nonzero frequency
 i(J(t0)) is periodic with a period
i(J(t0)) is periodic with a period  i =
2
i =
2 /
/ i(J(t0)). The period of the system must therefore be an
integer multiple ki of each of the individual coordinate periods
i(J(t0)). The period of the system must therefore be an
integer multiple ki of each of the individual coordinate periods
 i. If the system is periodic with some set of integer multiples,
then it is also periodic with any common factors divided out. Thus
the period of the system is
i. If the system is periodic with some set of integer multiples,
then it is also periodic with any common factors divided out. Thus
the period of the system is  = (ki/d)
= (ki/d)  i where d is the
greatest common divisor of the integers ki.
i where d is the
greatest common divisor of the integers ki.
For a system with two degrees of freedom, a solution is periodic if
there exists a pair of relatively prime integers k and j such that k
 0(J(t0)) = j
0(J(t0)) = j  1(J(t0)). The period of the system is
1(J(t0)). The period of the system is
 = 2
= 2  j /
j /  0(J(t0)) = 2
0(J(t0)) = 2  k /
k /  1(J(t0)); the
frequency is
1(J(t0)); the
frequency is  0(J(t0)) / j =
0(J(t0)) / j =  1(J(t0)) / k. A
periodic motion on the 2-torus is illustrated in
figure 4.10.
1(J(t0)) / k. A
periodic motion on the 2-torus is illustrated in
figure 4.10.
If the frequencies  i(J(t0)) satisfy an
integer-coefficient relation sumi ni
i(J(t0)) satisfy an
integer-coefficient relation sumi ni  i(J(t0)) = 0, we say
that the frequencies satisfy a commensurability.
If there is no commensurability for any nonzero integer coefficients,
we say that the frequencies are linearly independent (with respect to
the integers) and the solution is quasiperiodic. One can prove
that for n incommensurate frequencies all solutions come arbitrarily
close to every point in the configuration space.8
i(J(t0)) = 0, we say
that the frequencies satisfy a commensurability.
If there is no commensurability for any nonzero integer coefficients,
we say that the frequencies are linearly independent (with respect to
the integers) and the solution is quasiperiodic. One can prove
that for n incommensurate frequencies all solutions come arbitrarily
close to every point in the configuration space.8
For a system with two degrees of freedom the solutions in a region
described by a particular set of action-angle variables are either
equilibrium solutions, periodic solutions, or quasiperiodic
solutions.9
For systems with more than two degrees of freedom there are
trajectories that are neither periodic nor quasiperiodic with n
frequencies. These are quasiperiodic with fewer frequencies and dense
over a corresponding lower-dimensional torus.
As we have seen, in action-angle coordinates the angles move with
constant angular frequencies, and the momenta are constant. Thus
surfaces of section in action-angle coordinates are particularly
simple. We can make surfaces of section for time-independent
two-degree-of-freedom systems or one-degree-of-freedom systems with
periodic drive. In the latter case, one of the angles in the
action-angle system is the phase of the drive.
We make surfaces of section by accumulating points in one
pair of canonical coordinates as the other coordinate goes through
some particular value, such as zero. If we plot the section points
with the angle coordinate on the abscissa and the conjugate momentum
on the ordinate then the section points for all trajectories lie on
horizontal lines, as illustrated in
figure 4.11.
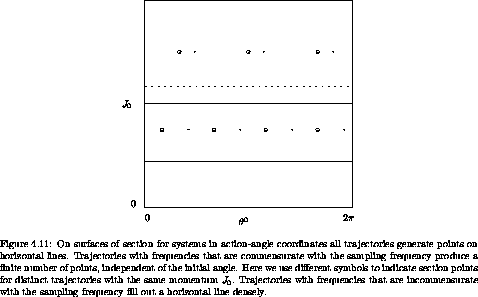
For definiteness, let the plane of the surface of
section be the ( 0, J0) plane, and the section condition be
0, J0) plane, and the section condition be
 1 = 0. The other momentum J1 is chosen so that all the
trajectories have the same energy. The momenta are all constant, so
for a given trajectory all points that are generated are constrained
to a line of constant J0.
1 = 0. The other momentum J1 is chosen so that all the
trajectories have the same energy. The momenta are all constant, so
for a given trajectory all points that are generated are constrained
to a line of constant J0.
The time between section points is the period of  1:
1:
 t = 2
t = 2 /
/  1(J(t0)) because a section point is generated
for every cycle of
1(J(t0)) because a section point is generated
for every cycle of  1. The angle between successive points on
the section is
1. The angle between successive points on
the section is  0(J(t0))
0(J(t0))  t =
t =  0(J(t0)) 2
0(J(t0)) 2  /
/
 1(J(t0)) = 2
1(J(t0)) = 2 
 (J(t0)), where
(J(t0)), where  (J) =
(J) =  0(J) /
0(J) /
 1(J) is called the rotation number of the trajectory.
Let
1(J) is called the rotation number of the trajectory.
Let  (i) and
(i) and  (i) be the ith point (i is an
integer) in a sequence of points on the surface of section generated
by a solution trajectory:
(i) be the ith point (i is an
integer) in a sequence of points on the surface of section generated
by a solution trajectory:
where the system is assumed to be on the section at t = t0.
Along a trajectory, the map from one section point (  (i),
(i),
 (i) ) to the next (
(i) ) to the next (
 (i + 1),
(i + 1),  (i + 1) ) is of the form:10
(i + 1) ) is of the form:10
As a function of the action on the section, the rotation number is
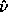 (
( (0)) =
(0)) =  (
( (0), J1(t0)), where J1(t0)
has the value required to be on the section, as for example by giving
the correct energy.
If the rotation number function
(0), J1(t0)), where J1(t0)
has the value required to be on the section, as for example by giving
the correct energy.
If the rotation number function 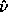 is strictly monotonic in the action coordinate
on the section then the map is called a twist map.11
is strictly monotonic in the action coordinate
on the section then the map is called a twist map.11
On a surface of section the different types of orbits generate
different patterns. If the orbit is an equilibrium solution then the
initial point on the surface of section is a fixed point. The system
just stays there.
If the two frequencies are commensurate, then the trajectory is
periodic and only a finite number of points are generated on the
surface of section. Both of the periodic solutions illustrated in
figure 4.10 generate two points on the
surface of section defined by  1 = 0. If the frequencies are
commensurate they satisfy a relation of the form k
1 = 0. If the frequencies are
commensurate they satisfy a relation of the form k
 0(J(t0)) = j
0(J(t0)) = j  1(J(t0)), where J(t0) = (
1(J(t0)), where J(t0) = ( (0), J1(t0)) is
the initial and constant value of the momentum tuple. The
motion is periodic with frequency
(0), J1(t0)) is
the initial and constant value of the momentum tuple. The
motion is periodic with frequency  0(J(t0))/j =
0(J(t0))/j =
 1(J(t0))/k, so the period is 2
1(J(t0))/k, so the period is 2 j/
j/
 0(J(t0)) = 2
0(J(t0)) = 2 k/
k/  1(J(t0)). Thus this
periodic orbit generates k points on this surface of section. For
trajectories with commensurate frequencies the rotation number is
rational:
1(J(t0)). Thus this
periodic orbit generates k points on this surface of section. For
trajectories with commensurate frequencies the rotation number is
rational: 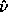 (
( (0)) =
(0)) =  (
( (0), J1(t0)) = j/k. The coordinate
(0), J1(t0)) = j/k. The coordinate  1 makes
k cycles while the coordinate
1 makes
k cycles while the coordinate  0 makes j cycles
(figure 4.10 shows a system with a
rotation number of 2/3). The frequencies depend on the momenta but
not on the coordinates, so the motion is periodic with the same period
and rotation number for all initial angles given these momenta. Thus
there is a continuous family of periodic orbits with different initial
angles.
0 makes j cycles
(figure 4.10 shows a system with a
rotation number of 2/3). The frequencies depend on the momenta but
not on the coordinates, so the motion is periodic with the same period
and rotation number for all initial angles given these momenta. Thus
there is a continuous family of periodic orbits with different initial
angles.
If the two frequencies are incommensurate, then the 2-torus
is filled densely. Thus the line on which the section points are
generated is filled densely. Again, this is the case for any initial
coordinates, because the frequencies depend only on the momenta.
There are infinitely many such orbits that are distinct for a given
set of frequencies.12
 -periodic). The configuration space described by n angles is an
n-torus. The momenta conjugate to these angles are called actions. Such phase-space coordinates are called action-angle
coordinates. We will see later how to reformulate systems in this
way.
Here we explore the consequences of such a formulation; this
formulation is especially useful for finding out what happens as
additional effects are added to integrable problems.
-periodic). The configuration space described by n angles is an
n-torus. The momenta conjugate to these angles are called actions. Such phase-space coordinates are called action-angle
coordinates. We will see later how to reformulate systems in this
way.
Here we explore the consequences of such a formulation; this
formulation is especially useful for finding out what happens as
additional effects are added to integrable problems. be the tuple of angles and J be the tuple of
conjugate momenta. The
be the tuple of angles and J be the tuple of
conjugate momenta. The 
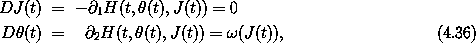
 (J) = D f(J) is a tuple of frequencies with a
component for each degree of freedom. The momenta are all constant
because the Hamiltonian does not depend on any of the coordinates. The motion
of the coordinate angles is uniform; the rates of change of the angles
are the frequencies
(J) = D f(J) is a tuple of frequencies with a
component for each degree of freedom. The momenta are all constant
because the Hamiltonian does not depend on any of the coordinates. The motion
of the coordinate angles is uniform; the rates of change of the angles
are the frequencies 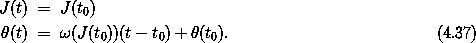
 i =
2
i =
2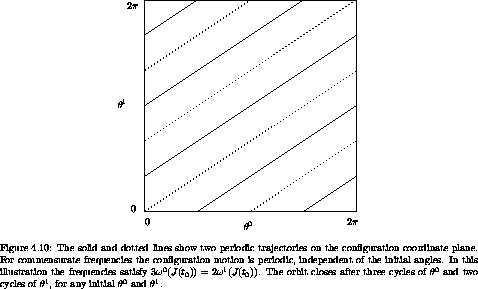

 t = 2
t = 2 (J(t0)), where
(J(t0)), where 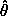 (i) and
(i) and  (i) be the ith point (i is an
integer) in a sequence of points on the surface of section generated
by a solution trajectory:
(i) be the ith point (i is an
integer) in a sequence of points on the surface of section generated
by a solution trajectory:

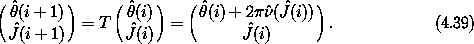
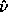 (
(