 (t) = ( t, q(t), p(t) ) is (F o
(t) = ( t, q(t), p(t) ) is (F o
 )(t) = F(t, q(t), p(t)). The time derivative of F o
)(t) = F(t, q(t), p(t)). The time derivative of F o
 is
is
Here we introduce the Poisson bracket, in terms of which
Hamilton's equations have an elegant and symmetric expression.
Consider a function F of time, coordinates, and momenta. The value
of F along the path  (t) = ( t, q(t), p(t) ) is (F o
(t) = ( t, q(t), p(t) ) is (F o
 )(t) = F(t, q(t), p(t)). The time derivative of F o
)(t) = F(t, q(t), p(t)). The time derivative of F o
 is
is
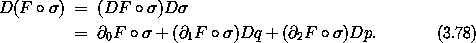
If the phase-space path is a realizable path for a system with Hamiltonian H, then Dq and Dp can be reexpressed using Hamilton's equations:
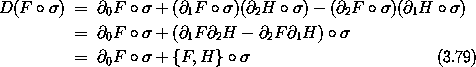
where the Poisson bracket { F , H } of F and H is defined by17

Note that the Poisson bracket of two functions on the phase-state space is also a function on the phase-state space.
The coordinate selector Q = I1 is an example of a function on phase-state space: Q(t, q, p) = q. According to equation (3.79),
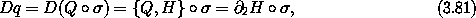
but this is the same as Hamilton's equation

Similarly, the momentum selector P = I2 is a function on phase-state space: P(t, q, p) = p. We have
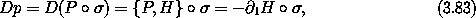
which is the same as Hamilton's other equation

So the Poisson bracket provides a uniform way of writing Hamilton's equations:

The Poisson bracket of any function with itself is zero, so we recover the conservation of energy for a system that has no explicit time dependence:
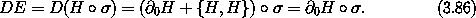
Let F, G, and H be functions of time, position, and momentum, and let c be independent of position and momentum.
The Poisson bracket is antisymmetric:

It is bilinear (linear in each argument):
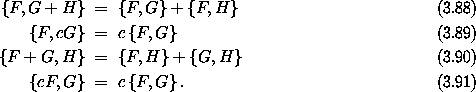
The Poisson bracket satisfies Jacobi's identity:
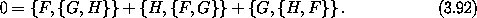
All but the last of (3.87-3.92) can immediately be verified from the definition. Jacobi's identity requires a little more effort to verify. We can use the computer to avoid some work. Define some literal phase-space functions of Hamiltonian type:
(define F
(literal-function 'F
(-> (UP Real (UP Real Real) (DOWN Real Real)) Real)))
(define G
(literal-function 'G
(-> (UP Real (UP Real Real) (DOWN Real Real)) Real)))
(define H
(literal-function 'H
(-> (UP Real (UP Real Real) (DOWN Real Real)) Real)))
Then we check the Jacobi identity:
(print-expression
((+ (Poisson-bracket F (Poisson-bracket G H))
(Poisson-bracket G (Poisson-bracket H F))
(Poisson-bracket H (Poisson-bracket F G)))
(up 't (up 'x 'y) (down 'px 'py))))
0
The residual is zero, so the Jacobi identity is satisfied for any three phase-space state functions with two degrees of freedom.
The Poisson bracket of conserved quantities is conserved.
Let F and G be time-independent phase-space state functions:
 0 F =
0 F =  0 G = 0. If F and G are conserved
by the evolution under H then
0 G = 0. If F and G are conserved
by the evolution under H then

So the Poisson brackets of F and G with H are zero: { F, H} = { G, H} = 0. The Jacobi identity then implies


so { F, G } is a conserved quantity. The Poisson bracket of two conserved quantities is also a conserved quantity.