be the configuration-path function;
(t) is the configuration at time t. The action of the
segment of the path in the time interval from t1 to t2
is7
Let us suppose that for each physical system there is a path-distinguishing function that is stationary on realizable paths. We will try to deduce some of its properties.
Our ordinary experience suggests that physical motion can be described by configuration paths that are continuous and smooth.3 We do not see the juggling pin jump from one place to another. Nor do we see the juggling pin suddenly change the way it is moving.
Our ordinary experience suggests that the motion of physical systems does not depend upon the entire history of the system. If we enter the room after the juggling pin has been thrown into the air we cannot tell when it left the juggler's hand. The juggler could have thrown the pin from a variety of places at a variety of times with the same apparent result as we walk through the door.4 So the motion of the pin does not depend on the details of the history.
Our ordinary experience suggests that the motion of physical systems is deterministic. In fact, a small number of parameters summarize the important aspects of the history of the system and determine its future evolution. For example, at any moment the position, velocity, orientation, and rate of change of the orientation of the juggling pin are enough to completely determine the future motion of the pin.
From our experience of motion we develop certain expectations about realizable configuration paths. If a path is realizable, then any segment of the path is a realizable path segment. Conversely, a path is realizable if every segment of the path is a realizable path segment. The realizability of a path segment depends on all points of the path in the segment. The realizability of a path segment depends on every point of the path segment in the same way; no part of the path is special. The realizability of a path segment depends only on points of the path within the segment; the realizability of a path segment is a local property.
So the path-distinguishing function aggregates some local property of the system measured at each moment along the path segment. Each moment along the path must be treated in the same way. The contributions from each moment along the path segment must be combined in a way that maintains the independence of the contributions from disjoint subsegments. One method of combination that satisfies these requirements is to add up the contributions, making the path-distinguishing function an integral over the path segment of some local property of the path.5
So we will try to arrange that the path-distinguishing function, constructed as an integral of a local property along the path, assumes an extreme value for any realizable path. Such a path-distinguishing function is traditionally called an action for the system. We use the word ``action'' to be consistent with common usage. Perhaps it would be clearer to continue to call it ``path-distinguishing function,'' but then it would be more difficult for others to know what we were talking about.6
In order to pursue the agenda of variational mechanics, we must invent
action functions that are stationary on the realizable
trajectories of the systems we are studying. We will consider actions
that are integrals of some local property of the configuration path at
each moment. Let be the configuration-path function;
(t) is the configuration at time t. The action of the
segment of the path in the time interval from t1 to t2
is7
where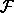 
[] is a function of time that measures some
local property of the path. It may depend upon
the value of the function at that time and the value of any
derivatives of at that time.8
The configuration path can be locally described at a moment in terms of the configuration, the rate of change of the configuration, and all the higher derivatives of the configuration at the given moment. Given this information the path can be reconstructed in some interval containing that moment.9 Local properties of paths can depend on no more than the local description of the path.
The function 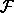measures some local property of the
configuration path .
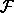We can decompose [] into
two parts: a part that measures some property of a local
description and a part that extracts a local description of the path
from the path function. The function that
measures the local property of the system depends on the particular
physical system; the method of construction of a local description of a
path from a path is the same for any system.
We can write 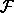[] as a composition of
these two functions:10
The function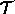 
takes the path and produces a function of
time whose value is an ordered tuple containing the time, the
configuration at that time, the rate of change of the configuration at
that time, and the values of higher derivatives of the path evaluated
at that time. For the path and time t:11
We refer to this tuple, which includes as many derivatives as are needed, as the local tuple.
The function 
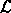depends on the specific details of the
physical system being investigated, but does not depend on any
particular configuration path. The function 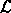computes a
real-valued local property of the path. We will find that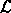
needs only a finite number of components of the local tuple to compute
this property: The path can be locally reconstructed from the full
local description; that 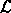depends on a finite number of
components of the local tuple guarantees that it measures a local
property.12
The advantage of this decomposition is that the local description of
the path is computed by a uniform process from the configuration path,
independent of the system being considered. All of the
system-specific information is captured in the function .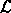
The function 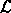is called a Lagrangian13
for the
system, and the resulting action,
is called the Lagrangian action. Lagrangians can be found for a great variety of systems. We will see that for many systems the Lagrangian can be taken to be the difference between kinetic and potential energy. Such Lagrangians depend only on the time, the configuration, and the rate of change of the configuration. We will focus on this class of systems, but will also consider more general systems from time to time.
A realizable path of the system is to be distinguished from others by having stationary action with respect to some set of nearby unrealizable paths. Now some paths near realizable paths will also be realizable: for any motion of the juggling pin there is another that is slightly different. So when addressing the question of whether the action is stationary with respect to variations of the path we must somehow restrict the set of paths we are considering to contain only one realizable path. It will turn out that for Lagrangians that depend only on the configuration and rate of change of configuration it is enough to restrict the set of paths to those that have the same configuration at the endpoints of the path segment.
The principle of stationary action14
asserts that for each dynamical system we can cook up a Lagrangian
such that a realizable path connecting the configurations at two
times t1 and t2 is distinguished from all conceivable paths by
the fact that the action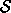 
[](t1, t2) is stationary with respect to variations of the
path. For Lagrangians that depend only on the configuration and rate
of change of configuration, the variations are restricted to those that
preserve the configurations at t1 and t2.15
Exercise 1.1. Fermat optics
Fermat observed that the laws of reflection and refraction could be
accounted for by the following facts: Light travels in a straight line
in any particular medium with a velocity that depends upon the medium.
The path taken by a ray from a source to a destination through any
sequence of media is a path of least total time, compared to
neighboring paths. Show that these facts imply the laws of
reflection and refraction.16
3 Experience with systems on an atomic scale suggests that at this scale systems do not travel along well defined configuration paths. To describe the evolution of systems on the atomic scale we employ quantum mechanics. Here, we restrict attention to systems for which the motion is well described by a smooth configuration path.
4 Extrapolation of the orbit of the Moon backward in time cannot determine the point at which it was placed on this trajectory. To determine the origin of the Moon we must supplement dynamical evidence with other physical evidence such as chemical compositions.
5 We suspect that this argument can be promoted to a precise constraint on the possible ways of making this path-distinguishing function.
6 Historically, Huygens was the first to use the term ``action'' in mechanics, referring to ``the effect of a motion.'' This is an idea that came from the Greeks. In his manuscript ``Dynamica'' (1690) Leibniz enunciated a ``Least Action Principle'' using the ``harmless action,'' which was the product of mass, velocity, and the distance of the motion. Leibniz also spoke of a ``violent action'' in the case where things collided.
7 A definite integral of a real-valued function f of a real
argument is written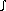 
ab f. This can also be written 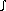ab
f(x) dx . The first notation emphasizes that a function is being
integrated.
8 Traditionally, square brackets are put around functional
arguments. In this case, the square brackets remind us that the value
of 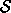may depend on the function in complicated ways,
such as through its derivatives.
9 In the case of a real-valued function, the value of the function and its derivatives at some point can be used to construct a power series. For sufficiently nice functions (real analytic), the power series constructed in this way converges in some interval containing the point. Not all functions can be locally represented in this way. For example, the function f(x) = exp( - 1/x2), with f(0) = 0, is zero and has all derivatives zero at x = 0, but this infinite number of derivatives is insufficient to determine the function value at any other point.
10 Here o denotes composition of
functions: (f o g)(t) = f(g(t)). In our notation the application
of a path-dependent function to its path is of higher precedence than
the composition, s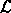o 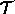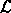o [] = o
([]).
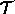11 The derivative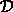 
of a configuration path
can be defined in terms of ordinary derivatives by specifying
how it acts on sufficiently smooth real-valued functions f of
configurations. The exact definition is unimportant at this stage.
If you are curious see footnote 23.
12 We will later discover that an initial segment of the local tuple is sufficient to determine the future evolution of the system. That a configuration and a finite number of derivatives determine the future means that there is a way of determining all of the rest of the derivatives of the path from the initial segment.
13 The classical Lagrangian plays a fundamental role in the path-integral formulation of quantum mechanics (due to Dirac and Feynman), where the complex exponential of the classical action yields the relative probability amplitude for a path. The Lagrangian is the starting point for the Hamiltonian formulation of mechanics (discussed in chapter 3), which is also essential in the Schrödinger and Heisenberg formulations of quantum mechanics and in the Boltzmann-Gibbs approach to statistical mechanics.
14 The principle is often called the ``principle of least action'' because its initial formulations spoke in terms of the action being minimized rather than the more general case of taking on a stationary value. The term ``principle of least action'' is also commonly used to refer to a result, due to Maupertuis, Euler, and Lagrange, which says that free particles move along paths for which the integral of the kinetic energy is minimized among all paths with the given endpoints. Correspondingly, the term ``action'' is sometimes used to refer specifically to the integral of the kinetic energy. (Actually, Euler and Lagrange used the vis viva, or twice the kinetic energy.)
15 Other ways of stating the principle of stationary action make it sound teleological and mysterious. For instance, one could imagine that the system considers all possible paths from its initial configuration to its final configuration and then chooses the one with the smallest action. Indeed, the underlying vision of a purposeful, economical, and rational universe played no small part in the philosophical considerations that accompanied the initial development of mechanics. The earliest action principle that remains part of modern physics is Fermat's principle, which states that the path traveled by a light ray between two points is the path that takes the least amount of time. Fermat formulated this principle around 1660 and used it to derive the laws of reflection and refraction. Motivated by this, the French mathematician and astronomer Pierre-Louis Moreau de Maupertuis enunciated the principle of least action as a grand unifying principle in physics. In his Essai de cosmologie (1750) Maupertuis appealed to this principle of ``economy in nature'' as evidence of the existence of God, asserting that it demonstrated ``God's intention to regulate physical phenomena by a general principle of the highest perfection.'' For a historical perspective on Maupertuis's, Euler's, and Lagrange's roles in the formulation of the principle of least action, see [28].
16 For reflection the angle of incidence is equal to the angle of reflection. Refraction is described by Snell's law: when light passes from one medium to another, the ratio of the sines of the angles made to the normal to the interface is the inverse of the ratio of the refractive indices of the media. The refractive index is the ratio of the speed of light in the vacuum to the speed of light in the medium.