5.13  Projects

Exercise 5.32.  Hierarchical Jacobi coordinates
A Hamiltonian for the n-body problem is

with

and

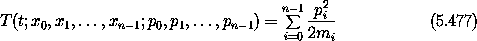
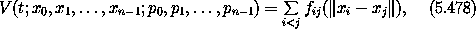
where x_i is the tuple of rectangular coordinates for body i and p_i is the tuple of conjugate linear momenta for body i.

The potential energy of the system depends only on the relative positions of the bodies, so the relative motion decouples from the center of mass motion. In this problem we explore canonical transformations that achieve this decoupling.

a.  Canonical heliocentric coordinates. The coordinates transform as follows:

where X is the center of mass of the system, and

for i>0, the differences of the position of body i and the body with index 0 (which might be the Sun). Find the associated canonical momenta using an F₂-type generating function. Show that the potential energy can be written solely in terms of the coordinates for i>0. Show that the kinetic energy is not in the form of a sum of squares of momenta divided by mass constants.

b.  Jacobi coordinates. The Jacobi coordinates isolate the center of mass motion, without spoiling the usual diagonal quadratic form of the kinetic energy. Define X_i to be the center of mass of the bodies with indices less than or equal to i:

The Jacobi coordinates are defined by

for 0 < i < n, and

The coordinates x'_i for 0 < i< n are the difference of the position of body i and the center of mass of bodies with lower indices; the coordinate x'₀ is the center of mass of the system. Complete the canonical transformation by finding the conjugate momenta using an F₂-type generating function. Show that the kinetic energy can still be written in the form

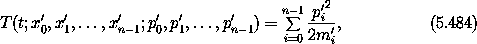
for some constants m'_i, and that the potential V can be written solely in terms of the Jacobi coordinates x'_i with indices i > 0.

c.  Hierarchical Jacobi coordinates. Define a ``body'' as a tuple of a mass and a rectangular position tuple. An n-body ``system'' is a tuple of n bodies: (b₀, b₁, ... , b_n-1). Define a ``linking'' transformation _jk for bodies j and k that takes an n-body system and returns a new linked system:

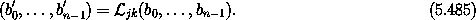
The bodies in the new system are the same as the bodies in the old system b_i' = b_i except for bodies j and k:

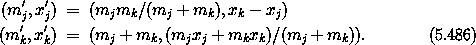
This is a transformation to relative coordinates and center of mass for bodies j and k. Extend this transformation to phase space and show that it preserves the form of the kinetic energy

Show that the transformation to Jacobi coordinates of part b is generated by a composition of linking transformations:

Interpret the coordinate transformation produced by such a succession of linking transformations; why do we call this a ``linking'' transformation? What requirement has to be satisfied for a composition of linking transformations to isolate the center of mass of the system (make it one of the coordinates)? Taking this constraint into account, find hierarchical Jacobi coordinates for a system with six bodies, arranged as two triple systems, each of which is a binary plus a third body. Verify that one of the coordinates is the center of mass of the system, and that the kinetic energy remains a sum of squares of the momenta divided by an appropriate mass constant.

Exercise 5.33.  Symplectic Integration
Consider a system for which the Hamiltonian H can be split into two parts, H₀ and H₁, each of which describes a system that can be efficiently evolved:

Symplectic integrators construct approximate solutions for the Hamiltonian H from those of H₀ and H₁.

We construct a map of the phase space onto itself in the following way (see Wisdom [47]). Define ₂(t) to be an infinite sum of Dirac delta functions, with interval 2,

with Fourier representation

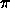Recall that a 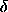function has the property that 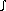_-a^a f 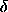= f(0) for any positive a and continuous real-valued function f. It is fruitful to think of the delta function as a limit of a function 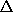_h that has the value 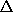_h(t) = 1/h in the interval - h/2 < t < h/2 and zero otherwise. Now consider the mapping Hamiltonian

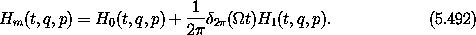
The evolution of the system between the delta functions is governed solely by H₀. To understand how the system evolves across the delta functions think of the delta functions in terms of 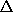_h as h goes to zero. Hamilton's equations contain terms from H₁ with the factor 1/h, which is large, and terms from H₀ that are independent of h. So as h goes to zero, H₀ makes a negligible contribution to the evolution. The evolution across the delta functions is governed solely by H₁. The evolution of H_m is obtained by alternately evolving the system according to the Hamiltonian H₀ for an interval 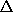t = 2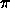 / 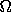and then evolving the system according to the Hamiltonian H₁ for the same time interval. The longer-term evolution of H_m is obtained by iterating this map of the phase space onto itself. Fill in the details to show this.

In terms of Lie series, the evolution of H_m for one delta function cycle 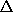t is generated by

The evolution of H_m approximates the evolution of H. Identify the noncommuting operator A with L_H0 and B with L_H1. Use the Baker-Campbell-Hausdorff identity (equation 5.475) to deduce that the local truncation error (the error in the state after one step 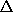t) is proportional to (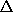 t)². The mapping is a first-order integrator.

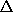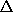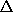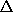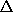By merely changing the phase of the delta functions, we can reduce the truncation error of the map, and the map becomes a second-order integrator. Instead of making a map by alternating a full step t governed by H₀ with a full step t governed by H₁, we can make a map by evolving the system for a half step t / 2 governed by H₀, then for a full step t governed by H₁, and then for another half step t / 2 governed by H₀. In terms of Lie series the second-order map is generated by

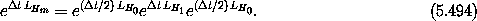
Confirm that the Hamiltonian governing the evolution of this map is the same as the one above but with the phase of the delta functions shifted. Show that the truncation error of one step of this second-order map is indeed proportional to (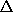 t)³.

Consider the Hénon-Heiles system. We can split the Hamiltonian into two solvable Hamiltonians in the following way (Wisdom [48]):

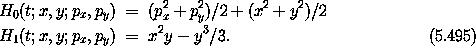
Hamiltonian H₀ is the Hamiltonian of two uncoupled linear oscillators; Hamiltonian H₁ is a nonlinear coupling. The trajectories of the systems described by each of these Hamiltonians can be expressed in closed form. Write programs that implement first-order and second-order maps for the Hénon-Heiles problem. Examine the evolution of the energy for both chaotic and quasiperiodic initial conditions. How does the magnitude of the energy error scale with the step size; is this consistent with the order of the integrator deduced above? How does the energy error grow with time? Generate surfaces of section using the second-order map. Does the map preserve the chaotic or quasiperiodic character of trajectories?