The Euler angles provide a convenient way to parameterize the
orientation of a rigid body. However, the equations of motion derived
for them have singularities. Though we can avoid the singularities by
using other Euler-like combinations with different singularities, this
kludge is not very satisfying. Let's brainstorm a bit and see if we
can come up with something better.
What does it take to specify an orientation? Perhaps we can take a
hint from Euler's theorem. Recall that Euler's theorem states that
any orientation can be reached with a single rotation. So one idea to
specify the orientation of a body is to parameterize this single
rotation that does the job. To specify this rotation we need to
specify the rotation axis and the amount of rotation. We contrast
this with the Euler angles, which specify three successive rotations.
These three rotations need not have any relation to the single
composite rotation that gives the orientation. Isn't it curious that
the Euler angles make no use of Euler's theorem?
We can think of several ways of specifying a rotation. One way would
be to specify the rotation axis by the latitude and the longitude at which
the rotation axis pierces a sphere. The amount of rotation needed to
take the body from the reference position could be specified by one
more angle. We can predict, though, that this choice of coordinates
will have similar problems to those of the Euler angles: if the amount
of rotation is zero, then the latitude and longitude of the rotation
axis are undefined. So the Lagrange equations for these angles are
probably singular. Another idea, without this defect, is to represent
the rotation by the rectangular components of an orientation vector
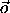 ; we take the direction of the orientation vector to be the
same as the axis of rotation that takes the body from the reference
orientation to the present orientation, and the length of the
orientation vector is the angle by which the body must be rotated, in
a right-hand sense, about the orientation vector. With this choice of
coordinates, if the angle of rotation is zero then the length of the
vector is zero and has no unwanted direction. This choice looks
promising.
; we take the direction of the orientation vector to be the
same as the axis of rotation that takes the body from the reference
orientation to the present orientation, and the length of the
orientation vector is the angle by which the body must be rotated, in
a right-hand sense, about the orientation vector. With this choice of
coordinates, if the angle of rotation is zero then the length of the
vector is zero and has no unwanted direction. This choice looks
promising.
We denote the rectangular components of 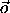 by the following: (
ox, oy, oz ); these will be our
generalized coordinates. The magnitude o =
(ox2 + oy2 + oz2)1/2 is the
angle of rotation. The axis of the rotation is
by the following: (
ox, oy, oz ); these will be our
generalized coordinates. The magnitude o =
(ox2 + oy2 + oz2)1/2 is the
angle of rotation. The axis of the rotation is 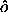 =
= 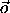 /
o. We denote the components of
/
o. We denote the components of 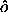 by
by 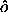 x,
x,
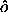 y, and
y, and 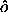 z. The first step in implementing the
components of the orientation vector as generalized coordinates is to
construct the rotation M to which the orientation vector
z. The first step in implementing the
components of the orientation vector as generalized coordinates is to
construct the rotation M to which the orientation vector 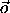 corresponds. Let
corresponds. Let 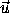 ' be a vector to one of the constituents of
the body in the reference orientation, and
' be a vector to one of the constituents of
the body in the reference orientation, and 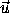 be the vector to
that constituent after rotation by M:
be the vector to
that constituent after rotation by M:
We can determine M by considering how the rotation represented by
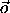 affects the vector
affects the vector 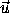 '. The component of
'. The component of 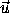 '
parallel to
'
parallel to 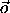 is unaffected. The perpendicular component is
reduced by the cosine of the rotation angle, and a component
perpendicular to these two is generated that is proportional to the
sine of the rotation angle and the magnitude of the perpendicular
component. Let (
is unaffected. The perpendicular component is
reduced by the cosine of the rotation angle, and a component
perpendicular to these two is generated that is proportional to the
sine of the rotation angle and the magnitude of the perpendicular
component. Let (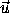 ')|| = (
')|| = (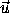 ' ·
' · 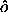 )
) 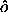 and
(
and
(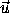 ')| =
')| = 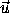 ' - (
' - (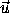 ')||; then
')||; then
From this expression we can construct the equivalent rotation matrix.
First define some useful primitive matrices:
and
with the identity
The matrix A is antisymmetric and S is the symmetric
outer product of the components of 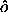 . The matrix A
implements the cross product of
. The matrix A
implements the cross product of 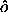 with other vectors, and the
matrix S projects vectors to the orientation vector. We have the
following identities:
with other vectors, and the
matrix S projects vectors to the orientation vector. We have the
following identities:
In terms of these matrices, the rotation matrix is
The inverse of a rotation is a rotation about the same axis but by the
negative of the rotation angle. Thus the inverse of M can be
written down immediately:
We verify that the inverse of the rotation matrix is the transpose of
the rotation matrix by recalling that I and S are
symmetric and A is antisymmetric.
The computation of the angular velocity vector from MT and
DM is straightforward, though tedious;
the angular velocity vector turns out to have a simple form:
The components of the angular velocity vector on the principal axes can be
found by multiplying the above by M-1 = MT:
Let
then we have
Solving, we find
The matrix W is not an orthogonal matrix, so its inverse is
not trivial, but we can use the properties of the primitive matrices
to find it. Suppose we have a matrix of the form
that we wish to invert. Let's guess that the inverse matrix has a
similar form:
We wish to find the coefficients a', b', and c' so that NN-1 = I. We find three conditions on the coefficients:
with solution
We can now invert the matrix W, using its representation in
terms of primitive matrices, to find
Note that all terms have finite limits as o -->
0. There is, however, a new singularity. As o --> 2  two
of the denominators become singular, but there the zeros in the
numerators are not strong enough to kill the singularity. This is the
expected singularity that corresponds to the fact that at radius 2
two
of the denominators become singular, but there the zeros in the
numerators are not strong enough to kill the singularity. This is the
expected singularity that corresponds to the fact that at radius 2
 the orientation vector corresponds to no rotation, but
nevertheless specifies a rotation axis. This singularity is easy to
avoid: whenever the orientation vector develops a magnitude larger
than
the orientation vector corresponds to no rotation, but
nevertheless specifies a rotation axis. This singularity is easy to
avoid: whenever the orientation vector develops a magnitude larger
than  , simply replace it by the equivalent orientation vector
, simply replace it by the equivalent orientation vector
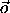 - 2
- 2
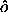 .
.
We can write the equations governing the evolution of the orientation
as a vector equation in terms of 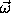 ' = M-1
' = M-1 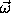 :
:
with two auxiliary functions
The equation of
motion for the orientation vector is surprisingly simple.
Both auxiliary functions have finite limits at zero:
Orientation vectors with
magnitude less than or equal to  are enough to specify all
orientations, and the equations of motion in this region have no
singularities. The orientation vector may develop magnitudes greater than
are enough to specify all
orientations, and the equations of motion in this region have no
singularities. The orientation vector may develop magnitudes greater than
 , but then we replace it by the equivalent orientation vector with
magnitude less than
, but then we replace it by the equivalent orientation vector with
magnitude less than  . And there is no hurry to do this because
the equations are not singular until the magnitude reaches 2
. And there is no hurry to do this because
the equations are not singular until the magnitude reaches 2 .
Thus we have a complete nonsingular specification of the rigid body
dynamics.
.
Thus we have a complete nonsingular specification of the rigid body
dynamics.
In order to use the orientation vector, we are presented with the practical
problem of converting between the orientation vector representation of
the orientation and other representations. We
can consider the rotation matrix M as an intermediate
universal representation. Whatever generalized coordinates have been
chosen, we must be able to compute the rotation matrix to which the
coordinates correspond. We must also solve the converse problem -- the
determination of the generalized coordinates from the rotation matrix.
We already have the explicit form for the rotation matrix in terms of
the orientation vector in
equation (2.118), repeated here for
convenience:
We can solve the converse problem by examining this same equation. We
note that of the contributions to M two parts are symmetric
and one is antisymmetric. We can isolate the antisymmetric component
by subtracting the transpose. We have
But the matrix A is simply related to the orientation vector:
We use the inverse operation A-1 that extracts
the components of a 3-vector from an antisymmetric 3 × 3 matrix. So we
have
Note that information about the magnitude o of the rotation is not
available in A by itself. However, the combination of M and its transpose produces a scaled version of A from
which the magnitude of the rotation can be recovered:
The length of the vector represented by the components on the
left-hand side is just sin o. This does not
determine o uniquely, because o spans
the interval 0 to  .
To completely determine o and thus
.
To completely determine o and thus 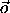 we need more
information, say by determining cos o.
we need more
information, say by determining cos o.
We can get cos o easily
enough. Examination of the components shows
Having determined both the sine and the cosine of o, we can determine
o. Some of these expressions contain divisions by o that
may be zero, but if o = 0 then the orientation vector is just the zero
vector. This completes the solution of the practical problem of going
to and from the orientation vector.
We can ask the following question: ``To which rotation does the
composition of two rotations correspond?'' Or alternatively, ``What is the algebra of orientation
vectors?'' We have all the
pieces; answering this question is just a matter of computation.
Given two rotations represented by the rotation matrices M1
and M2, the rotation matrix of the composition of these
rotations is M = M2 M1. Each of these rotation
matrices can be converted to the equivalent orientation vector. We
can define the composition 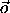 =
= 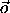 2 o
2 o 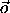 1.
1.
Let  = (sin o) / o, ß = (1 - cos o)/o2, and
= (sin o) / o, ß = (1 - cos o)/o2, and  =
cos o. By direct calculation we find
=
cos o. By direct calculation we find
and
which together determine 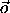 .
.
Well, the formulas are rather complicated, but it turns out that with
a little rearrangement they can be made quite simple. Let c
= cos ( o/2 ) and s = sin ( o/2),
and define 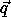 = (s / o)
= (s / o) 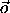 . The vector
. The vector
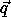 is a scaled version of
is a scaled version of 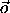 ; instead of having the
magnitude o as
; instead of having the
magnitude o as 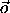 does, the vector
does, the vector 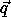 has the
magnitude s = sin (o/2). Notice that if o is
restricted to magnitudes less than
has the
magnitude s = sin (o/2). Notice that if o is
restricted to magnitudes less than  then the magnitude of the
rotation o can be recovered from the magnitude of
then the magnitude of the
rotation o can be recovered from the magnitude of
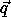 . Thus, with this restriction,
the vector
. Thus, with this restriction,
the vector 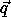 corresponds to a unique rotation, and no extra
information is needed. Nevertheless, it is convenient to keep track of
the cosine of the half-angle as well as the sine; so let q =
c = cos ( o/2).22
The magnitude of
corresponds to a unique rotation, and no extra
information is needed. Nevertheless, it is convenient to keep track of
the cosine of the half-angle as well as the sine; so let q =
c = cos ( o/2).22
The magnitude of 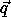 = s
and q = c, so q2 +
= s
and q = c, so q2 + 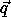 ·
· 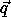 = 1. We can
reexpress the formulas for the composition of two rotations in terms
of
= 1. We can
reexpress the formulas for the composition of two rotations in terms
of 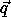 and q for each rotation. We have
and q for each rotation. We have

Now that is a significant simplification! The 4-tuple formed from
q with the three components of 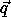 is the tuple of components of
Hamilton's
quaternion. We see that the vector part of the
quaternion that represents an orientation is a scaled version
of the orientation vector.
is the tuple of components of
Hamilton's
quaternion. We see that the vector part of the
quaternion that represents an orientation is a scaled version
of the orientation vector.
Hamilton discovered an even more elegant way of writing the
formula for the composition of two rotations. Introduce three unit quaternions
i, j, k, such that i2 = j2 = k2 = - 1, ij = k, jk = i,
ki = j, and each pair of distinct unit quaternions anticommute: ij = - ji, and
so on. Denote the three components of 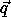 by ( q1, q2, q3 ),
and q by q0. Then define the composite quaternion q = q0
+ i q1 + j q2 + k q3. With the rule for how the unit quaternions
multiply, the formula for the composition of two rotations becomes
simply a multiplication. The quaternions generalize the idea of
complex numbers. In fact, they are the only algebraically closed field
besides complex numbers.
The unit quaternions cannot be represented simply as real numbers or
complex numbers, particularly because of their anticommuting
properties. However, they do have a representation as 2 × 2 matrices of
complex numbers. The units are
by ( q1, q2, q3 ),
and q by q0. Then define the composite quaternion q = q0
+ i q1 + j q2 + k q3. With the rule for how the unit quaternions
multiply, the formula for the composition of two rotations becomes
simply a multiplication. The quaternions generalize the idea of
complex numbers. In fact, they are the only algebraically closed field
besides complex numbers.
The unit quaternions cannot be represented simply as real numbers or
complex numbers, particularly because of their anticommuting
properties. However, they do have a representation as 2 × 2 matrices of
complex numbers. The units are

where the i on the right-hand side is the imaginary unit i2
= - 1. These matrices are related to the Pauli spin
matrices.
There are other representations, but further discussion of
representations of rotations would carry us too far afield.
If we are faced with the task of composing rotations repeatedly, then
the quaternions will be a handy intermediate representation. The
quaternions also have the advantage that we do not need to worry about
whether the angle of rotation is in the appropriate range. However,
the equation of motion for the orientation vector is simpler than the
equation of motion for the quaternion, so we will stick with the
orientation vector when we need nonsingular equations of motion for
the orientation.
Exercise 2.18. Composition
Verify that the rule for composition of two rotations in terms of the
orientation vectors
(equations 2.144 and
2.144) is
equivalent to the rule for multiplying two quaternions (equation
2.147).
Exercise 2.19. Equation of motion
Find the equation of motion for the orientation quaternion in terms of
the angular velocity vector.
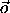 ; we take the direction of the orientation vector to be the
same as the axis of rotation that takes the body from the reference
orientation to the present orientation, and the length of the
orientation vector is the angle by which the body must be rotated, in
a right-hand sense, about the orientation vector. With this choice of
coordinates, if the angle of rotation is zero then the length of the
vector is zero and has no unwanted direction. This choice looks
promising.
; we take the direction of the orientation vector to be the
same as the axis of rotation that takes the body from the reference
orientation to the present orientation, and the length of the
orientation vector is the angle by which the body must be rotated, in
a right-hand sense, about the orientation vector. With this choice of
coordinates, if the angle of rotation is zero then the length of the
vector is zero and has no unwanted direction. This choice looks
promising.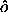 =
= 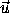 ' be a vector to one of the constituents of
the body in the reference orientation, and
' be a vector to one of the constituents of
the body in the reference orientation, and 
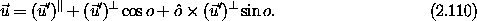
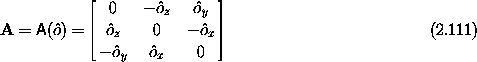



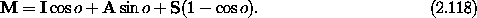
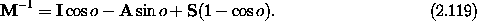
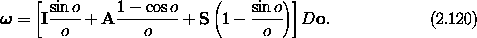
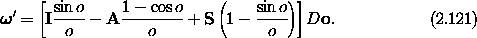
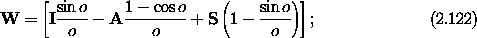





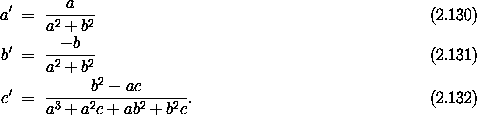
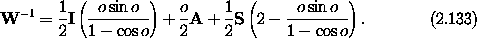
 two
of the denominators become singular, but there the zeros in the
numerators are not strong enough to kill the singularity. This is the
expected singularity that corresponds to the fact that at radius 2
two
of the denominators become singular, but there the zeros in the
numerators are not strong enough to kill the singularity. This is the
expected singularity that corresponds to the fact that at radius 2
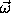 ' = M-1
' = M-1 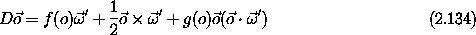


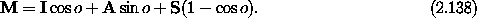




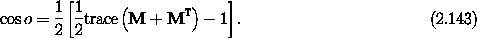
 = (sin o) / o, ß = (1 - cos o)/o2, and
= (sin o) / o, ß = (1 - cos o)/o2, and  =
cos o. By direct calculation we find
=
cos o. By direct calculation we find
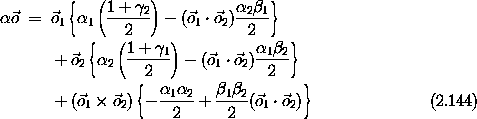
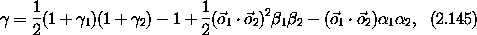
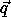 = (s / o)
= (s / o) 
